本記事では、流体による抵抗についてお話したいと思います。
先日、Twitterでこのようなアンケートを取りました。

↑画像です。
空気抵抗ってどういった式で表せるのか?
- 速度に比例するの?
それとも、 - 速度の2乗に比例するの?
結論を急ぎたい人はまとめを見てください!!
本記事では2018年の京都大学の問題を題材にしています。
※京都大学の問題そのものの解説をするのではありません。
あえて、大学の知識を広げながら高校生ではわからない部分を解説したいと思います。
流体における抵抗が速度にどのように依存するのかを解説する。
※問題を全て解くという解説ではなく、問題の意味を考える解説です。
京都大学は第問が3問あり、それを90分で解くことになります。
本記事は、その「第Ⅰ問:力学」の問題についての補足説明です。
力学の問題での心構え
せっかく京都大学という難関国立大学の問題を扱うので(そこまで扱ってない・・・)、力学の問題を解く際に受験生が意識しておくべきことを簡単にまとめておきたいと思います。
- 絵を描くこと
- 変数を何にするか決めること
- 立式する
- 変数と式の数が同じならあとは腕力で解く
- 単位(次元)を確認する
これについては下記の記事でも書いておきました。
基本的には、力学の問題は「運動方程式を記述」して、その運動方程式(偏微分方程式)を解くことで解が求まります。
解が求まるとは、「初期条件\(t=0\)の条件を与えると、運動方程式に従って、\(t\)秒での運動状態が定まる」ということを意味します。
運動状態とは、\(t\)秒での位置と速度(運動量)の組み合わせの事だと思ってもらって良いです。
だから、
- 求めたい変数を決める
- 運動方程式(あるいは力のつりあい)を書く
- 変数と立てた式が一致していることを確認する(→同じなら解ける!!)
- それを解く!!
この流れを意識することです。
2018年の京都大学の問題と解答の入手先
では、問題を以下から入手しましょう。
※代ゼミからダウンロードしました。
では、本題に移りましょう。
第1問の概要説明
京都大学の問題は基本的に穴埋め問題です。
なので多少大学の内容が入ってきても、丁寧な誘導問題であるため、高校生でも問題を解ききることは可能であると思います。
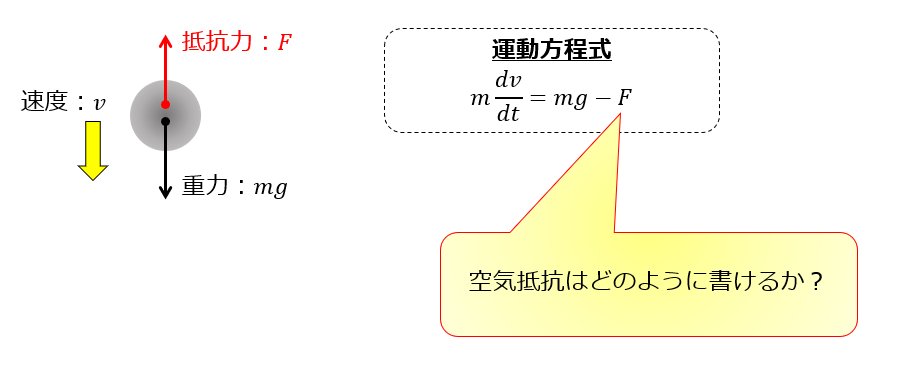
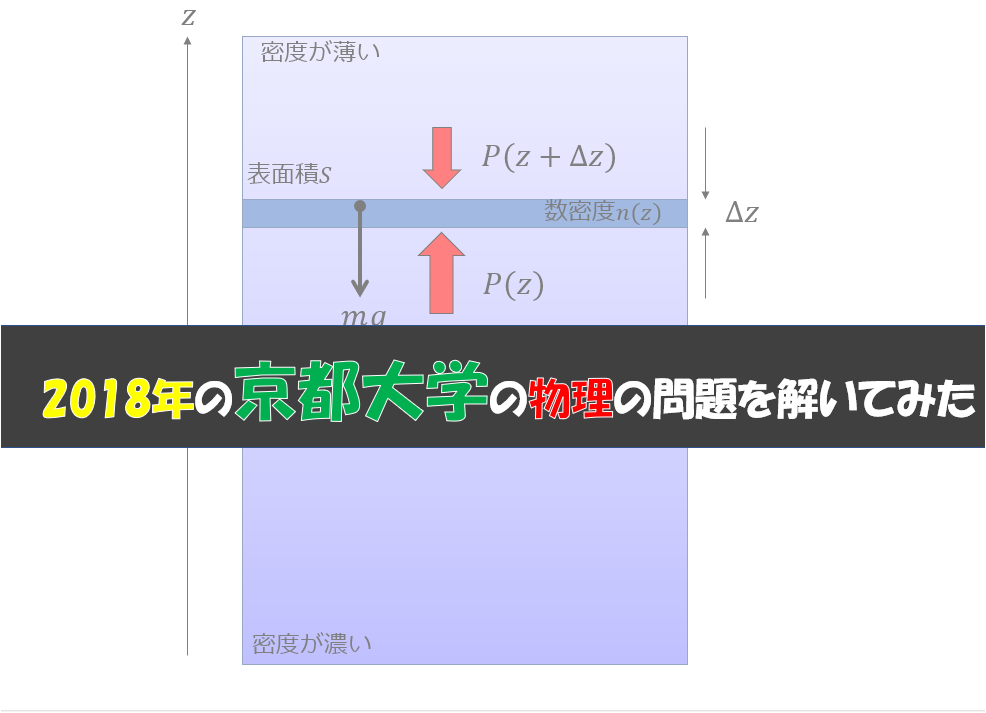
重力下にある物体が抵抗力を受けて鉛直方向下向きに落下する問題を解く
- 抵抗力が速度に比例する場合→(1)の問題
- 抵抗力が速度の2乗に比例する場合→(2)の問題
これらの問題を解くことになります。
冒頭でお話したように、物理の問題は解くべき方程式が与えらたらそれ数学の力を借りて、解を求めるということをします。
その与えられた方程式が大きなくくりでは偏微分方程式であり、ここでは運動方程式がそれにあたります。
京都大学の問題は基本的には穴埋め問題であるので、誘導に従えば高校生でも解答は可能だと思っていたのです・・・・が・・・・
ここでひとつ疑問が湧きます。
実現象は空気抵抗、すなわち流体における抵抗は、
流体における抵抗について・・・
- 速度に比例するのか?
- 速度の2乗に比例するのか?
これが気になりました。
もう、京都大学の問題を解くとかどうでもよくなってしまった(笑)
解いたけど・・
抵抗について皆はどのような認識か?:Twitterのアンケート結果
Twitterでアンケートを取ってみました(‘ω’)
結果は以下の通りです。
2018年の京都大学の物理の問題
・「抵抗が速度に比例する」
・「抵抗が速度の2乗に比例する」
というお話がありました。例えば球体のまわりの流れを考える場合とかを想像します。https://t.co/3jee07bc8X
— 宇宙に入ったカマキリ@物理ブログ (@t_kun_kamakiri) 2019年1月14日
「抵抗力なんて流れによって変わるだろ」って思われている方が大半ですね(‘ω’)
そうなんです。
抵抗力は流れによって変わるんです。
少なくとも僕が流体力学を勉強したことが間違っていなければ・・・
これについては、2つほど解説を用意しました。
- 抗力係数から抵抗を考える
- 次元解析から抵抗を考える
では、順にみていきましょう(^^)/
流体による抵抗
1.抗力係数から抵抗を考える
無次元量の抗力係数\(C_{d}\)を考えます。
※\(\rho\):密度
※\(U\):代表速度
※\(A\):代表面積(球体なら、最大断面積)
\(A\)は形状に変わります。
この抗力係数\(C_{d}\)を縦軸に、横軸にレイノルズ数\(Re\)をとります。
そうすると、形状ごとに関係性が出てくるのです。
つまり、抗力係数\(C_{d}\)がレイノルズ数\(Re\)だけに依存します。
\(Re=\frac{UL}{\nu}\cdot\cdot\cdot (2)\)
※\(L\):代表長さ
※※\(U\):代表速度
※\(nu\):動粘性係数
こちらをご参考ください→流体力学の力学的相似性
レイノルズ数\(Re\)をざっくり説明します。
レイノルズ\(Re\)が小さいと場合
レイノルズ数が小さい場合は、\(Re=\frac{UL}{\nu}\)を見てわかる通り、分母が分子より目立っているということ・・・
つまり、粘性の影響がでかい・・・・あるいは、流速が遅いという状態です。
流れの状態は、穏やかな層流状態です。
あるところで流速が大きくなったとしても粘性によって、その速度の影響は遠くへは影響を及ぼさず馴染まされて、結局穏やかな流れを維持しているという状態です。
レイノルズ\(Re\)が大きいと場合
レイノルズ数が大きい場合は、\(Re=\frac{UL}{\nu}\)を見てわかる通り、分子が分母より目立っているということ・・・
つまり、粘性の影響が小さい・・・・あるいは、流速が早いという状態です。
流れの状態は、乱れた乱流状態です。
あるところで流速が大きい場合、粘性が相対的に小さいため、速度は慣性に従って色んなところに影響を及ぼし合って、しまいにはめちゃくちゃ乱れた流れになります。
抗力係数とレイノルズ数の関係性
定義した抗力係数\(C_{d}\)とレイノルズ数\(Re\)は形状ごとにだいたいどのような傾向になるのかは、実験でも流体解析でもわかっているんですよね。
例えば、球体の場合は下記のような関係です。
球体の場合

円柱の場合は、下記のような関係です。
円柱の場合
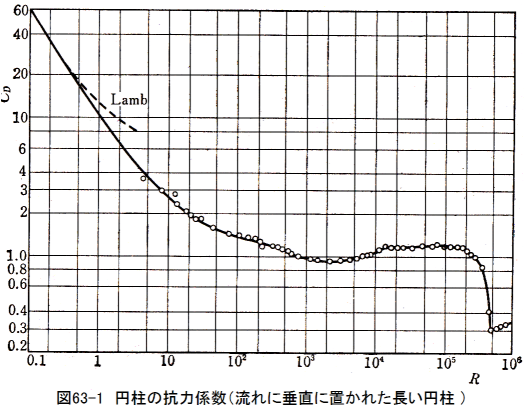
これについての詳しい解説はこちらのサイトがとても詳しいです。
これを見るとなんか、ざっくり小さなレイノルズ数と大きなレイノルズ数で関係性を式で表して表現できそうですよね。
抵抗は、
※\(C_{d}=\frac{F}{\frac{1}{2}\rho U^2A}\cdot\cdot\cdot (1)\)
※\(Re=\frac{UL}{\nu}\cdot\cdot\cdot (2)\)
球体の場合においては下記のようになります。
| レイノルズ数\(Re\) | 小さい場合 | 大きい場合 |
| 流れの状態 | 層流状態 | 乱流状態 |
| 抵抗力 | \begin{align*}C_{d}=\frac{24}{R}\cdot\cdot\cdot (4)\end{align*} なので、 \begin{align*}F=\frac{24\nu}{LU}\frac{1}{2}\rho U^2A \propto U\cdot\cdot\cdot (5)\end{align*} これは、ストークスの抵抗法則といいます。 |
\begin{align*}C_{d}=0.4\cdot\cdot\cdot ・(6)\end{align*} なので、 \begin{align*}F=0.4\frac{1}{2}\rho U^2A \propto U^2\cdot\cdot\cdot (7)\end{align*} これは、ニュートンの抵抗法則といいます。 |
| 抵抗力における 速度依存性 |
速度に比例する! | 速度の2乗に比例する! |
※レイノルズ数\(Re\)が小さい場合においての補足説明
ここでは実験や流体解析の事実から、抗力係数\(C_{d}\)とレイノルズ数\(Re\)の関係性がわかり、\(C_{d}=\frac{24}{R}\cdot\cdot\cdot (4)\)という近似式を使ったと思われる方がいるかもしれませんが、実はこれはむしろ理論計算から求めることができるものなのです。
抗力係数がわかるのではなくて、粘性が大きくて穏やかな流れであるので、「いきなり抵抗力を求めちゃえ」って感じで求めることができます。
結果だけ示しておきます。
球体の場合の抗力係数
ストークスの抵抗法則といいます。
つまり穏やかな流れで層流状態であれば、速度に比例するということです。
次元解析で考える
SI単位系での次元を次のようにおいて、それぞれの物理量の次元を書き下します。
質量:M
長さ:L
時間:S
温度:T
| 物理量 | 単位 | 次元 |
| 抵抗 | \(F\)[N] | \(LS^{-2}M\) |
| 速度 | \(U\)[m/s2] | \(LS^{-2}\) |
| 代表長さ | \(L\)[m] | \(L\) |
| 密度 | \(\rho\)[kg/m3] | \(ML^{-3}\) |
| 動粘性係数 | \(nu\)[m2/s] | \(L^{2}S^{-1}\) |
ここで、
- 粘性が重要な領域なのか?
- 密度変化が重要になってくる領域なのか?
この2つに分けてみます。
粘性が重要な領域(レイノルズ数が小さい領域)
粘性が重要な領域・・・・これはレイノルズ数が小さい場合の領域ですね。
とおきます。
これを両辺、単位があうように\(\alpha\)、\(\beta\)、\(\gamma\)を決めると・・・
\(\alpha=1\)、\(\beta=1\)、\(\gamma=1\)、\(\theta=1\)となります。
だから、(8)式は、
やっぱり、速度に比例します。
粘性が重要でない領域(レイノルズ数が大きい領域)
粘性が重要でない領域・・・・これはレイノルズ数が大きい場合の領域ですね。
粘性が重要でないならパラメータに入れないでおこう!!
これを両辺、単位があうように\(\alpha\)、\(\beta\)、\(\gamma\)を決めると・・・
\(\beta=1\)、\(\gamma=2\)、\(\theta=2\)、となります。
だから、(10)式は、
やっぱり、速度の2乗に比例します。
現実世界は?
理論上は流れによって、抵抗における速度依存性は変わるということがわかりました。
しかし、現実世界では「抵抗は速度の2乗に比例する場合」が多いでしょう。
というのも、だいたいチャリンコとか漕いだり、車を運転していても、どえらい風を顔面か車体に浴びているでしょう。
あれが、穏やかな流れ(層流状態)といえるのでしょうか(笑)
実世界のほとんどが乱流状態であるのだから「抵抗は速度の2乗に比例する場合」が多いと、個人的に結論づけています。
本記事でも書いてあるように、流れによって抵抗における速度依存性が変わるので、今どのような流れを想定しているかによって速度依存性を使い分けないといけないわけですね。
まとめ
流体における抵抗は、流れによって変化する
レイノルズ数が小さい場合(層流状態):抵抗は速度に比例する
レイノルズ数が大きい場合(乱流状態):抵抗は速度の2乗に比例する
2018年の京都大学の物理の問題
・「抵抗が速度に比例する」
・「抵抗が速度の2乗に比例する」
というお話がありました。例えば球体のまわりの流れを考える場合とかを想像します。https://t.co/3jee07bc8X
— 宇宙に入ったカマキリ@物理ブログ (@t_kun_kamakiri) 2019年1月14日
アンケートにご協力いただきました方々、ありがとうございました。
おかげで良い記事が書けました(‘ω’)























記事を楽しく読ませて頂きました。
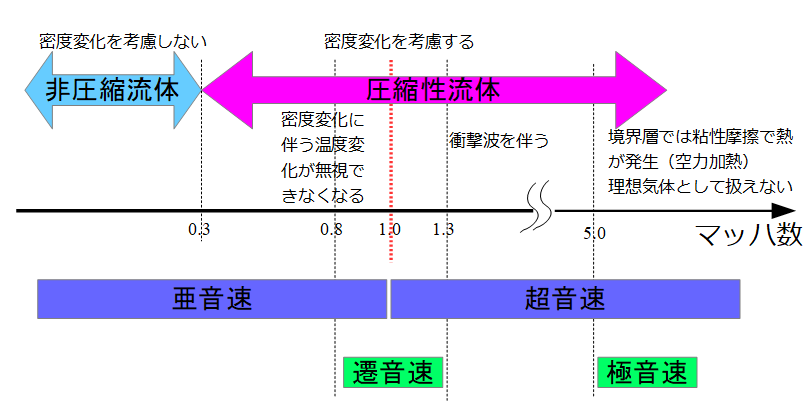
レイノルズ数Reが小さい場合の「流速が遅いというところから密度が一定として扱える非圧縮な流れもこの領域ですね(‘ω’)」という記述が少し気になります。
おそらく層流域ではだいたい非圧縮性流れとして扱える風速になるという意図なのだと思いますが、上記の文章だと非圧縮性流れならばだいたい層流として扱えるかのように誤解を与えるのではないかと思います。
非圧縮性流体として扱う(Ma4000)になることは多いです。
例えば人が立っていたときに、空気の動粘性係数1.5×10^-5[m2/s]、代表速度0.05[m/s](ほぼ無風)、代表長さ1.5[m](人の身長程度)の条件でMa=0.00015、Re=5000くらいになるります。空調分野では乱流域で非圧縮性流体として扱うのは一般的なので、細かい指摘かもしれないですが何かしら補足いただけるとありがたいです。
これからもいろいろな記事を楽しみにしています。
お読みいただきましてありがとうございます。
また、ご指摘ありがとうございます。
鋭い指摘で大変ありがたいです。
そうですよね。後の次元解析で「粘性が重要か密度が重要か・・・」という考察を書いているときに、勢いで書いてしまいましたm(_ _)m
非圧縮性の中でも層流、乱流とあるので、ここでの議論で密度変化(非圧縮かどうか)を取り入れるのはおかしいですね。
ありがとうございます。
>非圧縮性流体として扱う(Ma4000)
これはRe=4000ということでしょうか?
「密度変化しない非圧縮と仮定しても乱流はあります」といった指摘であると解釈しました。
記事全体を見渡すと、非圧縮かどうかは重要でないため、誤解を生みかねないのでそのような文言は削除しますね。
大変貴重なご意見ありがとうございました。
お早い対応ありがとうございます。
>非圧縮性流体として扱う(Ma4000)
ここは非圧縮性流体として扱う(Ma4000)と書くつもりでした。解釈いただいた内容であっています。失礼しました。
記事の本筋からはずれる指摘にもかかわらず対応いただきありがとうございました。
いえいえ。こちらこそありがとうございました。
またお気づきの点ありましたら、遠慮なくよろしくお願いします。