たまに趣味(?)で流体のコンピュータのシミュレーション(流体解析)をする者です。
流体解析って難しいですよね。
何が難しいって、
- 解析条件
- 境界条件
- タイムステップ
- 数値計算の離散化スキームの選択
など、数値計算特有の周辺知識もさることながら、そもそも今から解析する流体はどのような性質のものなのか?を把握していないと、どういった数理モデルで現象をシミュレーションで再現したいかがわからないのです。
そういう意味で、流体解析をするにあたってとても重要なことは「どのような流れの性質を持っているかを把握していることである」と思っています。
流れの性質については、色々ありますが代表的なところでいうと「非圧縮性や圧縮性」「層流や乱流」・・・あとは・・・色々です。
その流れの性質の中で特に、非圧縮性か圧縮性かはもっとも基本的な議論なのではないかと思っています。
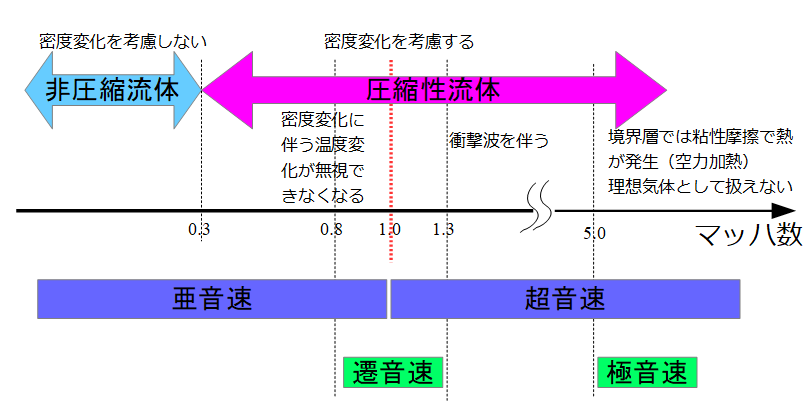
非圧縮性流体か圧縮性流体かはマッハ数を指標にするということをまとめる。
非圧縮性と圧縮性
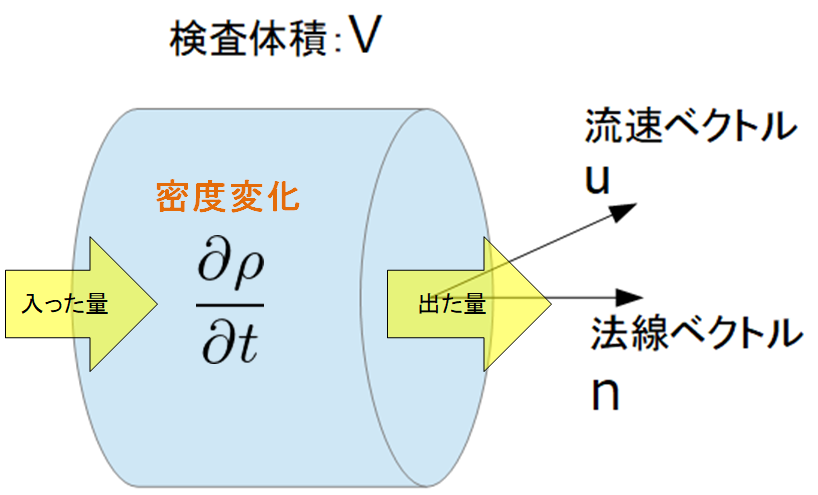
流体は、下の絵のように加圧(圧力を増加)や温度増加によって密度が上昇します。
つまり、流体は圧力や温度によって密度は変化する性質が基本的にあります。
これを、物質の圧縮性と言います。

このときに、密度の変化を考慮するか、考慮しないかで「圧縮性流体として取り扱うか」「非圧縮性流体として取り扱うか」が決まります。
表にしてみましょう。
勘違いしてはいけないのは、非圧縮性という流体が存在しているのではなくて、両者の区別は「あなたが密度変化を考慮しない流れ(非圧縮性)として現象を取り扱ったかどうか」ということに過ぎないのです。
本当はみ~んな圧縮性の流体なのですよってことですね。
密度の変化を考慮する、考慮しないはとても漠然とした考え方ですが、
ここで重要になる特徴量がマッハ数になります。
※\(a\):音速、\(u\):代表的な流速
結論
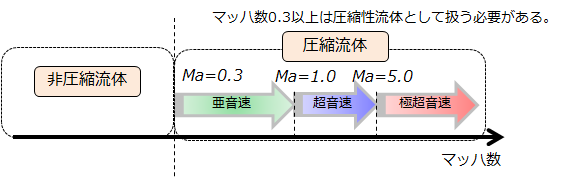
以下のことを覚えておきましょう。
このマッハ数0.3という数字はどこから来たのかと言いますと、
「流体の密度変化を5%以内を非圧縮性と見なす」というところから来ています。
絵で描くとこんな感じです。
まとめ
「非圧縮性流体や圧縮性流体」の違いについて簡単にまとめましたが、そこにはマッハ数がとても重要であることを見ました。
しかし、密度変化(密度伝播)には音速という物理量がとても重要な役割を演じています。
では、
- なぜ音速が密度変化に重要な役割を演じているのか?
- なぜ密度変化とマッハ数が関係しているのか?
- マッハ数とは物理的にどのような意味を持っているのか?
これらをまとめた記事がこちらです。
実現象をどんな数理モデルで再現しようとしているかを考えるのはとても重要
この「非圧縮性」「圧縮性」は流体解析でとても重要な知識であるため、きっちり理解しておきたいという思いがあります。
コンピュータのシミュレーションは、とりあえず設定してしまえば、どんなでたらめな設定でもとりあえず計算してしまうのです。
とても危険です。
じゃー、非圧縮性流体なんてめんどくさい区別なんてしなくて全ての流体を圧縮性流体で扱えば良いではないか?て思うかもしれませんが、それまた全て圧縮性流体として扱ってはとても計算効率が悪いです。
密度変化が5%以下の流体に対しては、非圧縮性として扱っても十分精度が出ることが検証されているようなので、計算コストを考えても非圧縮性流体として扱って良さそうな場合は、非圧縮性流体として扱ってしまいましょうというわけです。