よく非圧縮性の流体として取り扱っても良いかどうかに、マッハ数の大きさを指標にすることがあります。
非圧縮性の流体として扱うとは、
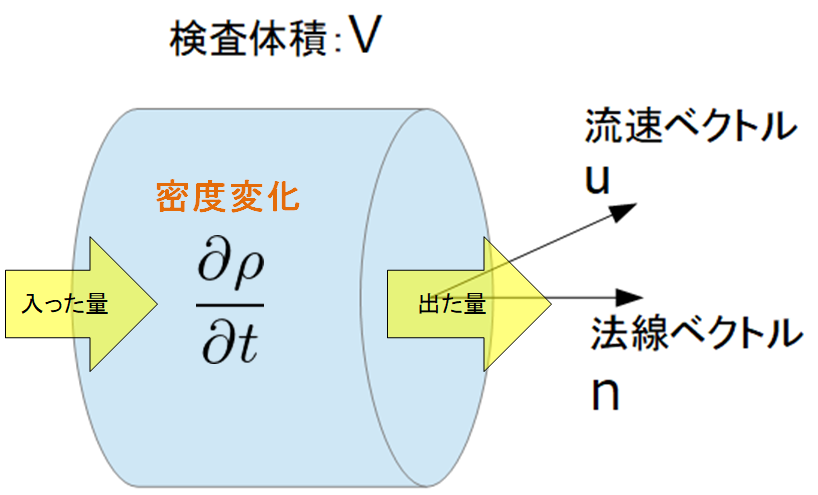
「流れに対して密度変化を無視できるかどうか」・・・(1)
であるのに対して、マッハ数とは定義が、
であります。
※\(u\):流速、\(u\):音速
どうも(1)(2)が結びつかないので、簡単に整理だけしたいと思います。
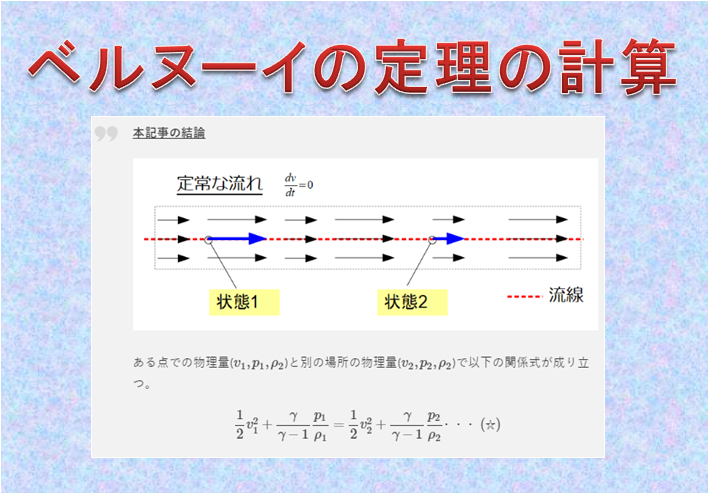
ベルヌーイの定理より
非圧縮性の流体におけるベルヌーイの定理によると、
となります。
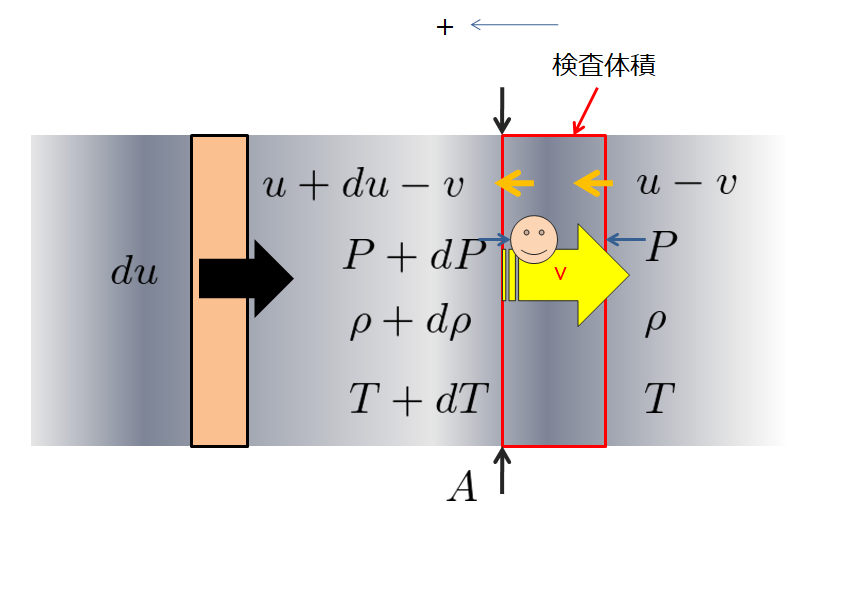
これは例えば、下記の絵のように「物体から離れたある点と、物体近辺で流速が0になっている(よどみ点)」での流線に対して成り立っていると考えてるエネルギー保存則を考えている場合にあたります。

(3)式に対して、\(\Delta p=p_{0}-p\)とすれば、
となります。
ここでは圧縮性が小さいとしています。
非圧縮性をある程度仮定しているという意味では、圧力の変動は音速で伝播するため、(圧力変動は)ほぼ一瞬で伝わります。
だから、\(\Delta p →0\)なので、\(dp\)と微小圧力変化として表記してよいでしょう。
そうすると、(4)式は、
となります。
ところで、音速の定義は、
だったから(流体の密度伝搬は音速で伝わる。圧縮性の考慮は音速と流速の大小関係が重要)、(5)式は、
ここで音速の定義(2)式を用いました。
ここでようやく(7)式で、密度変化率とマッハ数の関係式が(少々強引ではありますが)導けたことになります。
密度変化率が5%以下の時の、マッハ数は約0.3以下
では、密度変化率が5%以内としてた場合に、マッハ数が行く以下であるかを(7)式から計算してみれば良いことになります。
実際計算してみると、
と、約0.3くらいになります。
これにて、密度変化率が5%以下の場合はマッハ数は0.3以下であるということがわかりました。
マッハ数と0.3以下であれば非圧縮性として扱っても良いというよりは、今回のように密度変化率を何%以下にするかでマッハ数の指標を決める方が良いということに注意しなくてはいけません。
マッハ数0.3以下というのは、あくまでも一般論であります。
定性的な議論・・・・
↑こちらの記事で、「物理量の変動は音速で伝播する」などと書いておりますが、密度変動が無視できるかどうかというのは、音速と流速の大小に依るというのが定性的にもわかるでしょう。
「音速と流速の大小」というのは、すたわちマッハ数\(M=\frac{u}{a}\)のことであります。
流速が音速よりもずっと遅い場合は、その密度変動は音速で伝播するために、流速に乗った(流体粒子などと一緒に運動)場合には、その変動が全く見えないので、密度の変動は無視しても良い近似となっているはずです。
逆に、流速が音速に近づくと、流速に乗って(流体粒子などと一緒に運動)密度変動を観測すると、音速で伝播している密度変動もよく見えるようになるでしょう。(密度変動が目立つ)
だからマッハ数がいくつの流れを扱っているか、流速が音速と比較してどうであるかというのは、流れをどのように扱うか(非圧縮性として扱うか圧縮性として扱うか)の指標になる大切な無次元量であります。
具体的にどれくらいの流速なら非圧縮性流体として扱えるか
空気を例にとります。
常温であれば音速は約340m/sです。
そうすると、マッハ数0.3の流れというのは、流速が約100m/sの流れということになります。
航空機以外でこんなに速い流れなんてなかなかないかもしれません(笑)
ちなみに水での音速は常温で約1500m/sですので、なおさら水の圧縮性なんて考慮する必要もないということがわかります。