流体力学ラグランジュの渦定理【渦ができる要因を理解する】

どうも(^^)/

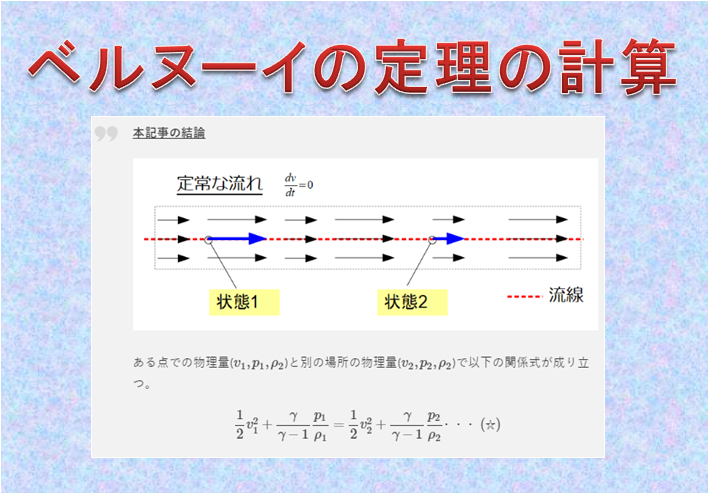
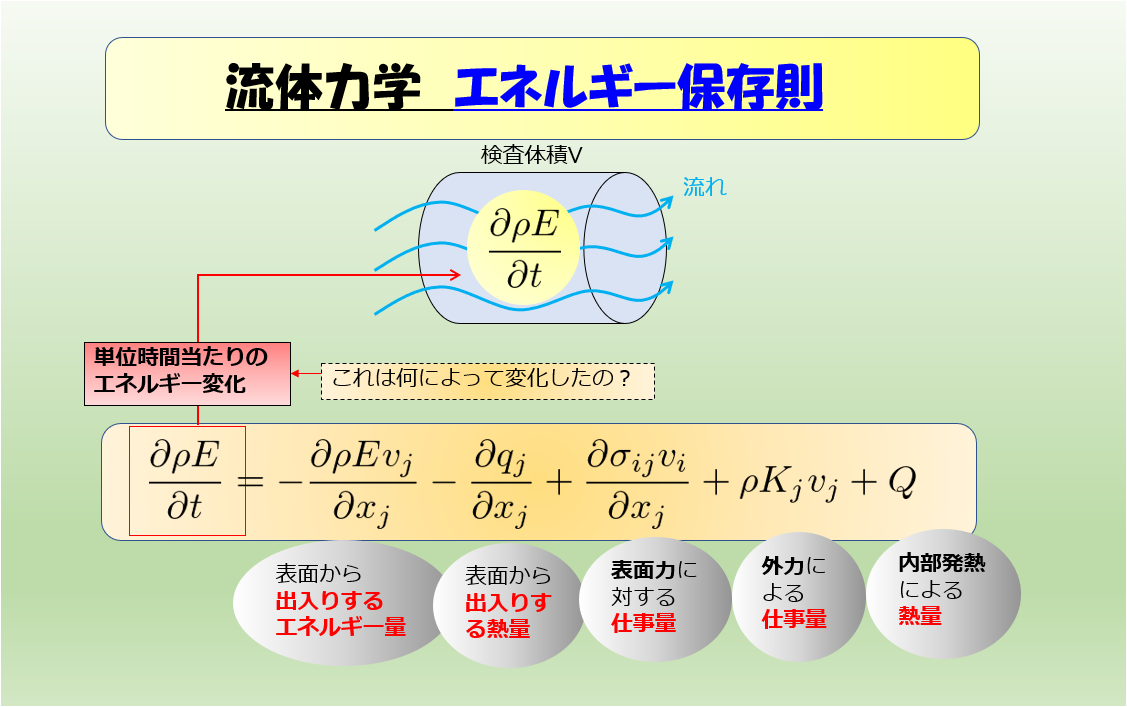
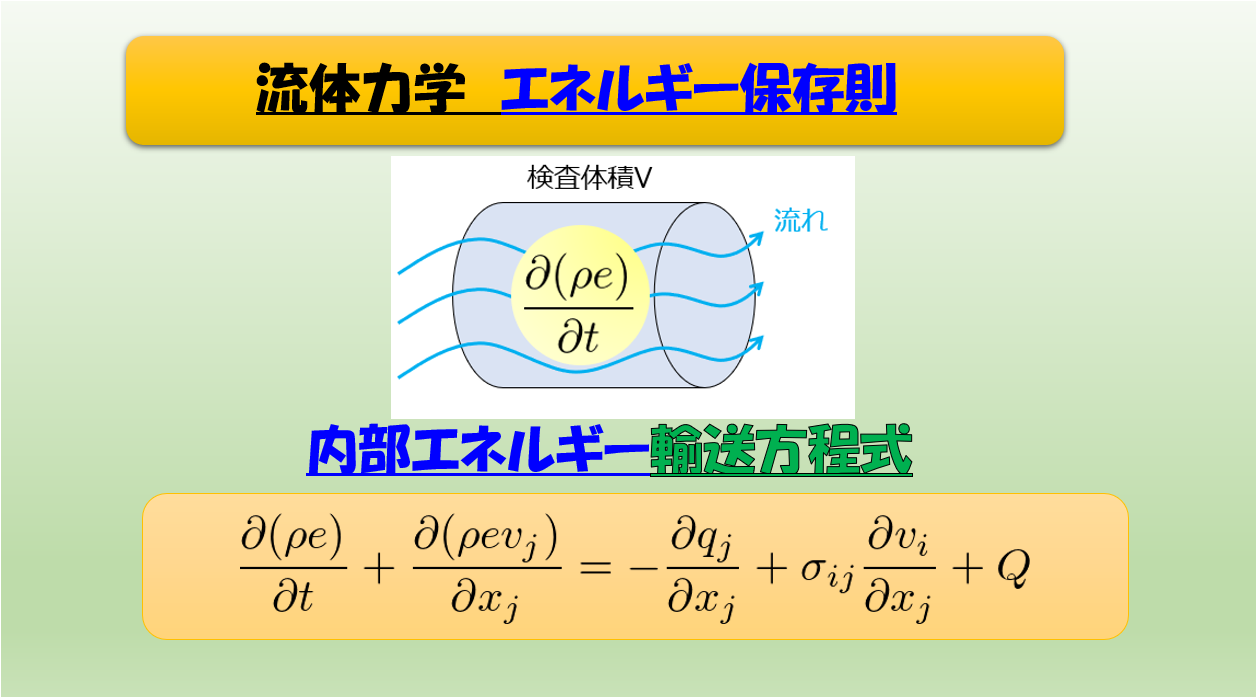
以前には下記のような記事を書いていきました。

ラグランジュの渦定理

ラグランジュの渦定理は、ケルビンの循環定理やヘルムホルツの渦定理と違って言葉で下記のような内容となっています。

ラグランジュの渦定理

下記のような条件であれば、渦は不生不滅である、

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

つまり、「初期状態で渦無しの流れであれば、その後もずっと渦無しの流れであり・・・初期に渦ありの流れであれば、その後もずっと渦ありの流れである（勝手に消滅しない）」ということを意味しています。
これが、ラグランジュの渦定理です。

ケルビンの循環定理と同じではないのか？

「初期状態で渦無しの流れであれば、その後もずっと渦無しの流れであり・・・初期に渦ありの流れであれば、その後もずっと渦ありの流れである（勝手に消滅しない）」

という言葉を見て、ケルビンの循環定理と同じことを言っているのではないか？

と思う人もいるかもしれませんが、実はちょっと意味合いが違います。

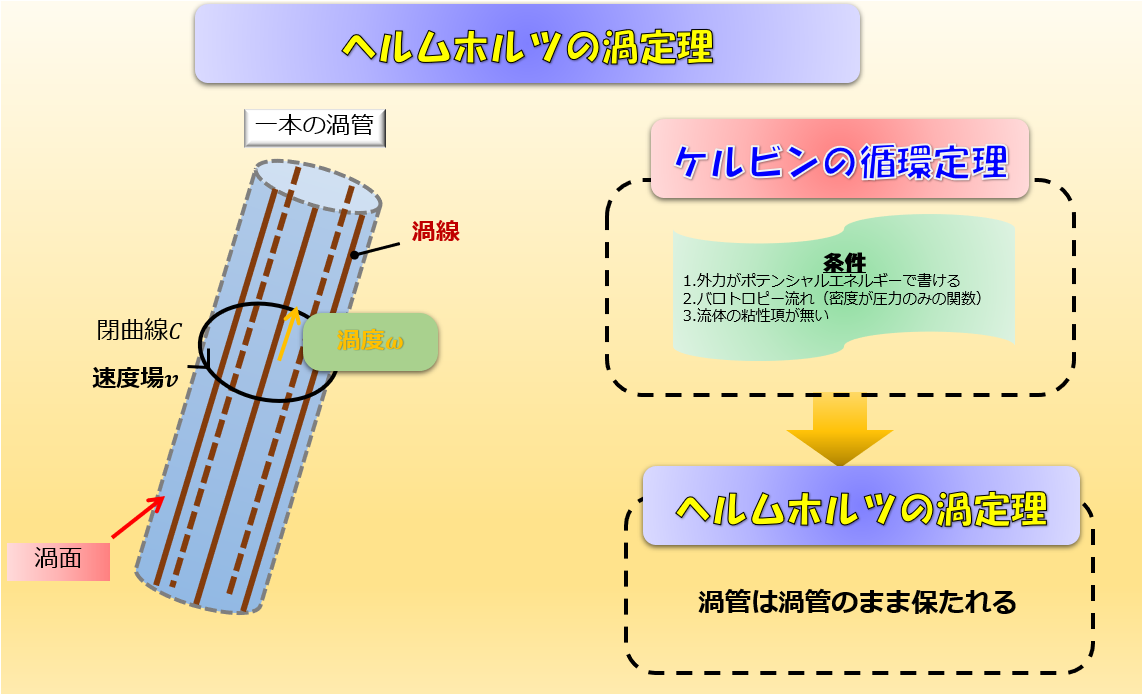
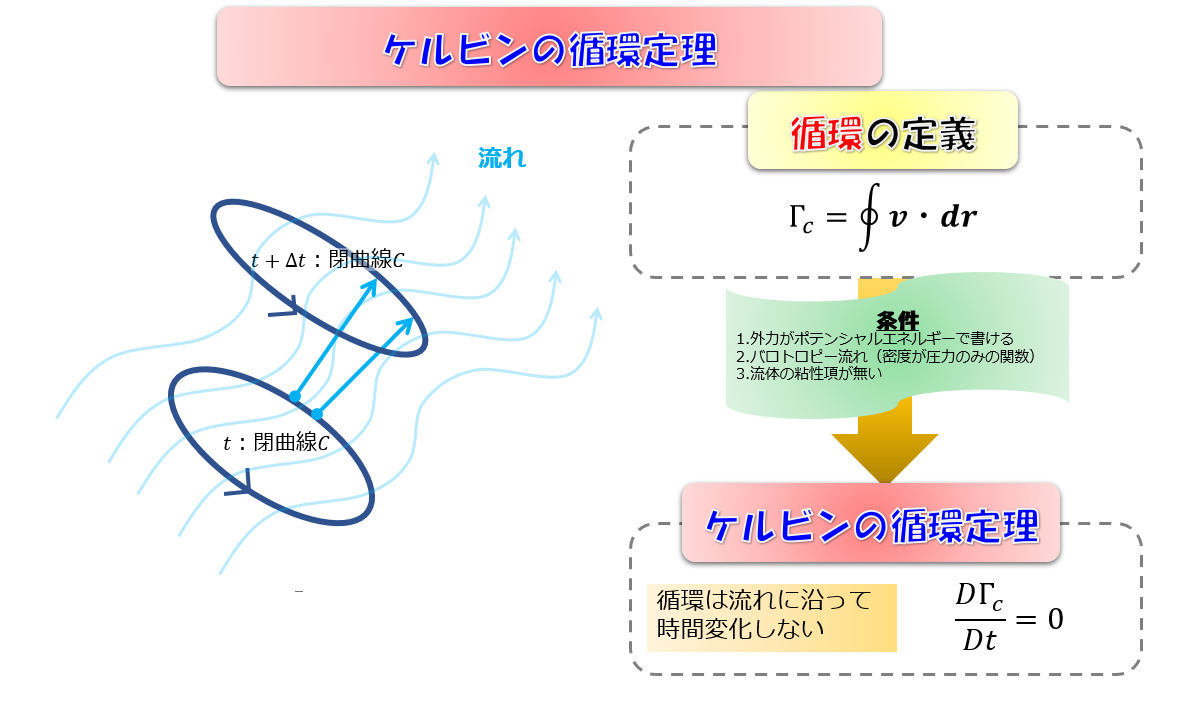
ケルビンの循環定理は、↓こちら。

ケルビンの循環定理

記の3つの条件を課すと、「流れに沿って変化する循環の時間変化を考えると、循環は変化しない」。

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

循環が変化しない（保存）

\begin{align*}
\frac{D\Gamma_{c}}{Dt}=0
\end{align*}

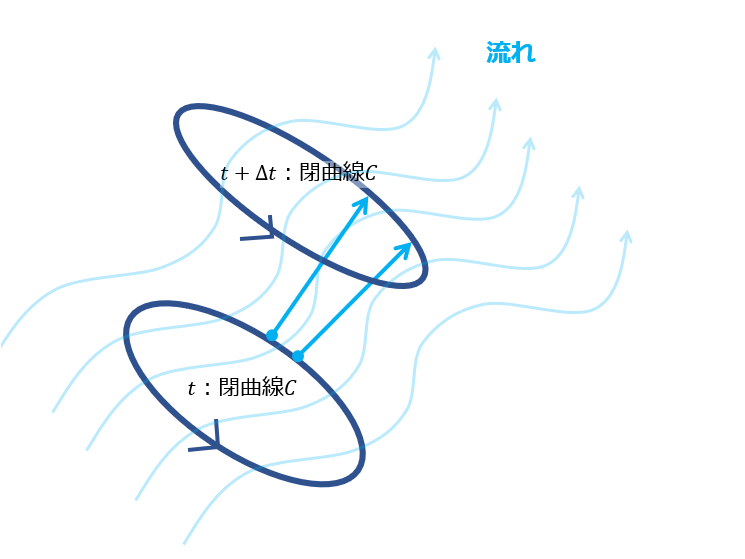
ケルビンの循環定理というのは循環が保存するということを言っているのですよね。

もし仮に、閉曲線内で渦度\(\boldsymbol{\omega}\)が一定値と簡単に考えた場合には、

循環は下記の絵のように考えることができます。

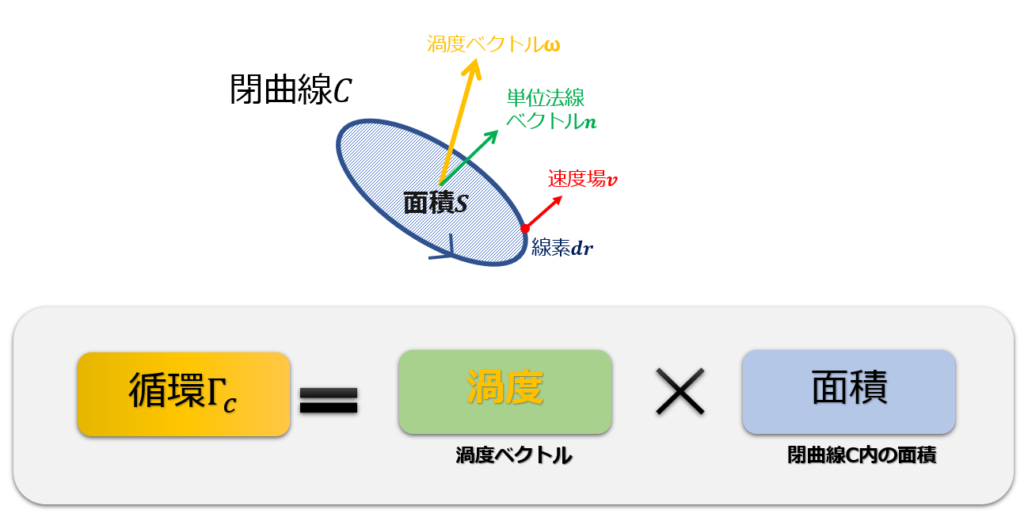
ということは、ケルビンの循環定理からは、循環が保存するということだけなので、

渦管の伸長など（極端な例で渦糸）で、渦度の大きさ自体は変わっているのですよね。

一方、ラグランジュの渦定理は、あくまでも下記の条件が揃っていれば、渦なし流れと渦あり流れは全く区別することができるという定性的なものです。

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

渦度などを議論したい場合は、やはりケルビンの循環定理やヘルムホルツの渦定理から述べた方が良いでしょう♪

逆に渦が生成消滅する条件は何か

渦が不生不滅である条件は、わかったと・・・では、その逆の渦が生成消滅する条件は何か？ということになると、下記の条件が成り立たないときですよね。

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

少し例を見てみましょう。

カルマン渦列

これは、流体の粘性がある場合の流れであるため、ケルビンの循環定理は成り立ちません。

ゆえに、渦無しの流れであっても、途中から渦ありの流れになっても構わないということになります。

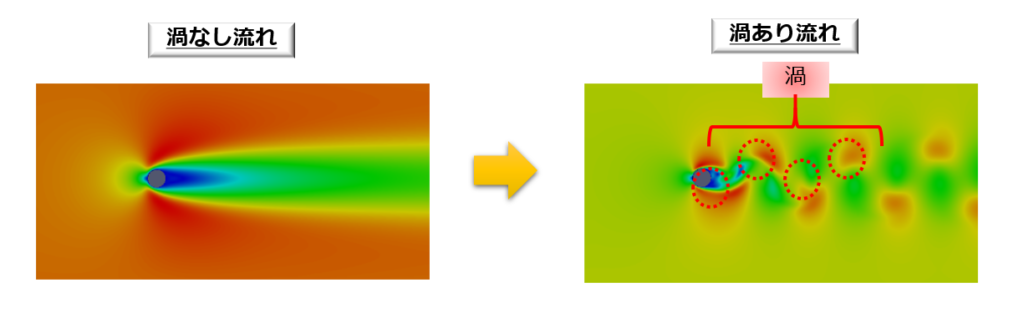
特に、円柱の壁側では粘性の影響がとても大きく、円柱の壁側から渦が生成しているのが見て取れます。

ケルビンヘルムホルツ不安定

こちらは粘性はもちろんのことながら、2相流（空気と水など）であり2相の界面には界面張力などのせん断力がはたらいています。

ですので、ケルビンの循環定理は成り立ちません。

ゆえに、渦無しの流れであっても、途中から渦ありの流れになっても構わないということになります。

まとめ

「初期状態で渦無しの流れであれば、その後もずっと渦無しの流れであり・・・初期に渦ありの流れであれば、その後もずっと渦ありの流れである（勝手に消滅しない）」ということを意味しています。
これが、ラグランジュの渦定理です。

ラグランジュの渦定理

下記のような条件であれば、渦は不生不滅である、

条件

外力がポテンシャルエネルギーで書ける\(\boldsymbol{K}=-\nabla U\)
バロトロピー流れ（密度が圧力のみの関数)\(\rho=f(p)\)
流体の粘性項が無い

粘性項が無視できるような流れの場合にはラグランジュの渦定理が適用できるということですが、壁など比較的粘性項が支配的になる領域ではラグランジュ渦定理は成り立たないため渦が生成したりします。

流体力学を深く理解するための参考書

初心者から中級者で流体力学を学ぶのにおすすめの参考書を以下に列挙しておきます。
流体力学は、「工学向け」か「理学向け」で内容が結構変わってきます。

工学部向け流体力学

工学向けでは以下の3冊をお勧めします。

流体力学 (JSMEテキストシリーズ)

日本機械学会

5,000円(12/10 17:57時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

👆こちらは、初心者でもわかりやすく理解できると思います。

演習書としては以下のものが、難しすぎず・・・がっつり練習できます。

演習で学ぶ「流体の力学」入門第2版

孝夫, 西海, 隆義, 一柳

6,860円(12/10 11:15時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

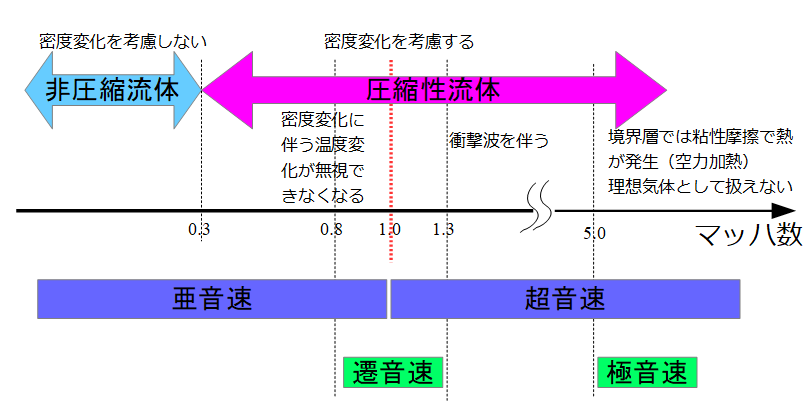
工学部であれば圧縮性の流体まで、学ぶことが多いと思いますので、「圧縮性流体」の参考書としては以下の書籍がお勧めです。

圧縮性流体力学―内部流れの理論と解析

松尾一泰

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

理学部向け流体力学

僕は、理学部出身なので主に愛用していた書籍を紹介します。

流体力学 (前編) (物理学選書 (14))

今井功

7,480円(12/10 11:15時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

👆こちらの書籍は流体力学を学ぶために一番最初に購入した本なのですが、今まで読んだ流体力学の中で一番わかりやすいと思っています。
ただ、残念過ぎるのは「前編」だけを書いて著者がお亡くなったため、「後編」がないという参考書です。それなのに絶版にならずに書籍で見かけるんですから、相当有名なんだろうなと思います。

もう少し優しい参考書としては「今井氏」の流体力学がお勧めですね。