標準k-εモデルのモデル定数の決定方法（Cμ=0.09は覚えておく)

こんにちは（@t_kun_kamakiri）
本記事では、乱流モデルの1つである標準$k$-$\epsilon$モデルにおけるモデル定数の決定方法について解説をします。

まず、本記事で示したい内容は以下です。

モデル定数の決定方法

標準$k$-$\varepsilon$モデルにおいて、乱流渦動粘性 $\nu_{t} = C_{\nu}\frac{k^2}{\varepsilon}$を決めるために必要な残りの2方程式は以下となります。

\begin{align*}
\frac{\partial k}{\partial t} + U_j \frac{\partial k}{\partial x_j} &= P_k – \varepsilon+ \frac{\partial}{\partial x_j} \bigg\{\left( \nu + \frac{\nu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j} \bigg\}\\
\frac{\partial \varepsilon}{\partial t} + U_j \frac{\partial \varepsilon}{\partial x_j} &= C_{\varepsilon 1} \frac{\varepsilon}{k} P_k – C_{\varepsilon 2} \frac{\varepsilon^2}{k} + \frac{\partial}{\partial x_j} \bigg\{\left( \nu + \frac{\nu_t}{\sigma_\varepsilon} \right) \frac{\partial \varepsilon}{\partial x_j} \bigg\}
\end{align*}

モデル定数は$C_{\mu}=0.09, \sigma_{k}=1.0, \sigma_{\varepsilon}=1.3, C_{\varepsilon 1}=1.44, C_{\varepsilon 2}=1.92$

モデル定数は$C_{\mu}=0.09, \sigma_{k}=1.0, \sigma_{\varepsilon}=1.3, C_{\varepsilon 1}=1.44, C_{\varepsilon 2}=1.92$が用いられる背景を正確に覚える必要がありませんが、大枠の流れは覚えておくと良いでしょう。

局所平衡：$C_{\mu}$の決定
一様等方乱流の減衰：$C_{\varepsilon 2}$の決定
乱流境界層中
まとめ
参考書
計算力学技術者資格のための問題アプリ

局所平衡：$C_{\mu}$の決定

乱れの運動エネルギー$k=\frac{\over{u^{\prime}u^{\prime}}}{2}$の方程式は、

\begin{align*}
\frac{\partial k}{\partial t} + \frac{\partial k\overline{u}_{j}}{\partial t}=P_{k}-\varepsilon+\frac{\partial}{\partial x_{j}}\bigg\{\big(\nu+\frac{\nu_{\tau}}{\sigma_{k}}\big)\frac{\partial k}{\partial x_{j}}\bigg\}
\end{align*}

平均速度勾配による乱れエネルギーの生成$P_{k}$は、

\begin{align*}
P_{k} \equiv \frac{1}{2}P_{ii}&=-\tau_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}\\
&=\nu_t \left( \frac{\partial \bar{U}_i}{\partial x_j} + \frac{\partial \bar{U}_j}{\partial x_i} \right) \frac{\partial \bar{U}_i}{\partial x_j}
\end{align*}

ここで、レイノルズ応力$\tau_{ij}=\overline{u_{i}^{\prime}u_{j}^{\prime}}=\frac{2}{3}k\delta_{ij}-2\nu_{t}\overline{D}_{ij}$、平均流速の速度勾配の1次積$\overline{D}_{ij}=\frac{1}{2}\left( \frac{\partial \bar{U}_i}{\partial x_j} +\frac{\partial \bar{U}_j}{\partial x_i} \right)$を使っています。

【レイノルズ応力とは】レイノルズ平均モデルでの乱れによるせん断力でもレイノルズ応力について解説していますが、参考書によっては$\overline{u_{i}^{\prime}u_{j}^{\prime}}$をレイノルズ応力と言ったり、$-\rho \overline{u_{i}^{\prime}u_{j}^{\prime}}$をレイノルズ応力と言ったりします。
単位を考えると、応力は$\text{Pa}=\text{N}/\text{m}^2=\text{kg}\cdot\text{m}/\text{s}^2$なので、$-\rho \overline{u_{i}^{\prime}u_{j}^{\prime}}$がレイノルズ応力としては用語として正しいと思います。

エネルギー散逸率$\varepsilon$は、

\begin{align*}
\varepsilon\equiv \frac{1}{2}\varepsilon_{ii}=\nu\overline{\frac{\partial u_{i}^{\prime}}{\partial x_{j}}\frac{\partial u_{i}^{\prime}}{\partial x_{j}}}
\end{align*}

平行平板間や円管内の乱流の乱れエネルギーについて、$y$は壁に垂直な方向として局所平衡条件$P_{k}\simeq \varepsilon$を課すと、

\begin{align*}
P_{k}&=-\tau_{ij}\frac{\partial \overline{u}}{\partial x}\\
&=\nu_{\tau}\frac{\partial \overline{u}}{\partial y}\frac{\partial \overline{u}}{\partial y}\\
&=C_{\mu}\frac{k^2}{\varepsilon}\frac{\partial \overline{u}}{\partial y}\frac{\partial \overline{u}}{\partial y}
\end{align*}

ここで標準$k$-$\epsilon$モデルにおけるレイノルズ応力が$\tau=\nu_{\tau}\frac{\partial \overline{u}}{\partial y}$であることを使用しています。

これより、

\begin{align*}
C_{\mu}=\frac{\varepsilon^2}{k^2(\frac{d\bar{u}}{dy})^2}=\bigg(\frac{u_{\tau}^2}{k}\bigg)^2\simeq 0.091
\end{align*}

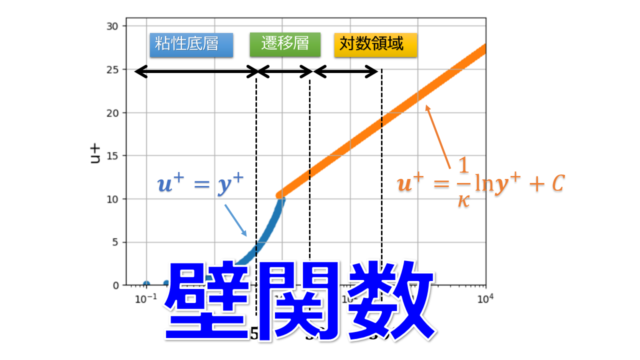
※上記の式は、$y^{+}>60$の対数領域で摩擦速度$k=3.3u\_{\tau}^2$、$\varepsilon=\frac{u\_{\tau}^3}{ky}$と書けることが実測結果で得られており、それを使用した。

局所平衡条件と乱流エネルギーと摩擦速度の2乗の比の2乗により$C_{\mu}=0.09$が決定されています。

一様等方乱流の減衰：$C_{\varepsilon 2}$の決定

一様等方乱流においてエネルギー保有渦における乱流エネルギーの散逸率$\varepsilon$は、乱流によって、乱流エネルギーが時間とともに散逸によって減少することを示しています。

\begin{align*}
\frac{dk}{dt}=-\varepsilon
\end{align*}

一様等方乱流の減衰において、完全に発達した乱流では$\varepsilon$は空間に依らないため、エネルギー散逸の方程式は、

$\frac{\partial \varepsilon}{\partial t}=-C_{\varepsilon 2}\frac{\varepsilon^2}{k}$

ここから、減衰の初期の過程において、$k\propto t^{-1}$より、

\begin{align*}
\frac{d^2k}{dt^2}=-C_{\varepsilon 2}\frac{\varepsilon^2}{k}=C_{\varepsilon 2}\frac{(\frac{dk}{dt})^2}{k}=C_{\varepsilon 2}t^{-3}
\end{align*}

を得ます。

さらに、2階微分して$\frac{d^2 k}{d t^2}\propto 2t^{-3}$なので、$C_{\varepsilon 2}=2$を得ます。

実際は実験によって$C_{\varepsilon 2}=1.92$が用いられます。

一様等方乱流の減衰過程により$C_{\varepsilon 2}=1.92$が決定されています。

乱流境界層中

平均圧力勾配のない平板境界層では、$\frac{D \varepsilon}{D t}$と局所平衡$P_{k}\simeq \varepsilon$が成り立ちます。

まず、

\begin{align*}
P_{k}=\nu_{\tau}\frac{d\bar{u}}{dy}\frac{d\bar{u}}{dy}=-\overline{u^{\prime}v^{\prime}}\frac{d\bar{u}}{dy}=u_{\tau}^2\frac{u_{\tau}}{\kappa y}
\end{align*}

と局所平衡$P\_{k}\simeq \varepsilon$より$\varepsilon=\frac{u\_{\tau}^3}{\kappa y}$を得ます。

さらに$\frac{D \varepsilon}{D t}$より、粘性項は無視して、

\begin{align*}
0=C_{\varepsilon 1}C_{\mu}k^2\big(\frac{d\bar{u}}{dy}\big)^2-C_{\varepsilon 2}\frac{\varepsilon^2}{k}+\frac{d}{dy}\big(\frac{\nu_{\tau}}{\sigma_{\varepsilon}}\big)
\end{align*}

代入して整理すると、

\begin{align*}
C_{\varepsilon 1}-C_{\varepsilon 2}=\frac{\kappa^2}{\sigma_{\varepsilon}\sqrt{C_{\mu}}}
\end{align*}

を得ます。

ここで、カルマン定数$\kappa=0.41$と先ほど決定した$C_{\mu}=0.09,C_{\varepsilon 2}=1.92$を用い、実験的に$C_{\varepsilon 1}=144, \sigma_{\varepsilon }=1.3$と決定されます。

$\sigma_{k}$は種々の乱流の計算結果と計測値との一致より$\sigma_{k}=1$が用いられます。

まとめ

ざっくりにモデル定数の決定を整理しておきましょう。

局所平衡条件と乱流エネルギーと摩擦速度の2乗の比の2乗により$C_{\mu}=0.09$が決定
一様等方乱流の減衰過程により$C_{\varepsilon 2}=1.92$が決定
平板境界層の局所平衡$P_{k}\simeq \varepsilon$から$C_{\varepsilon 1}-C_{\varepsilon 2}=\frac{\kappa^2}{\sigma_{\varepsilon}\sqrt{C_{\mu}}}$により$C_{\varepsilon 1}=144, \sigma_{\varepsilon }=1.3$と決定
種々の乱流の計算結果と計測値との一致より$\sigma_{k}=1$