こんにちは(@t_kun_kamakiri)
本日は「計算力学技術者試験の熱流体2級」で出てくる壁関数の式を解説をします。
壁関数とは乱れた流れにおける壁側での速度分布のことです。
- 壁側での速度分布とはどういう分布なのか?
- 壁関数を考えるのか?
というのが気になるところでしょう。
壁関数は、乱れた流れを数値シミュレーションする際の壁側の境界条件として非常に重要になってきます。熱流体のCAE解析をする人は必ず知っておく必要があります。
- 計算力学技術者試験の熱流体2級を勉強している方
- 壁関数って何?という方
- $y^{+}$って何?という方
- 壁関数を考える理由を知りたい方
※微分や偏微分などは理解している方を対象にしています。
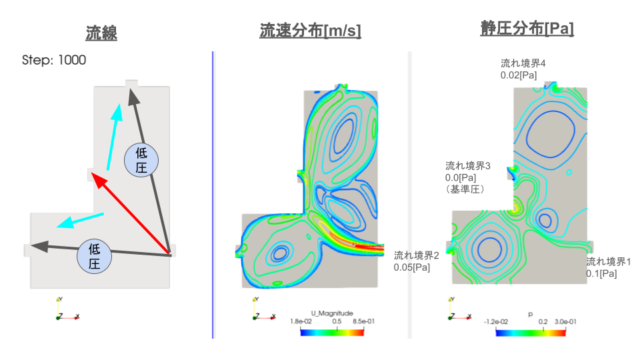
では、問題です。
問題の解説は本記事に書いています。
解答はまとめに書いています。
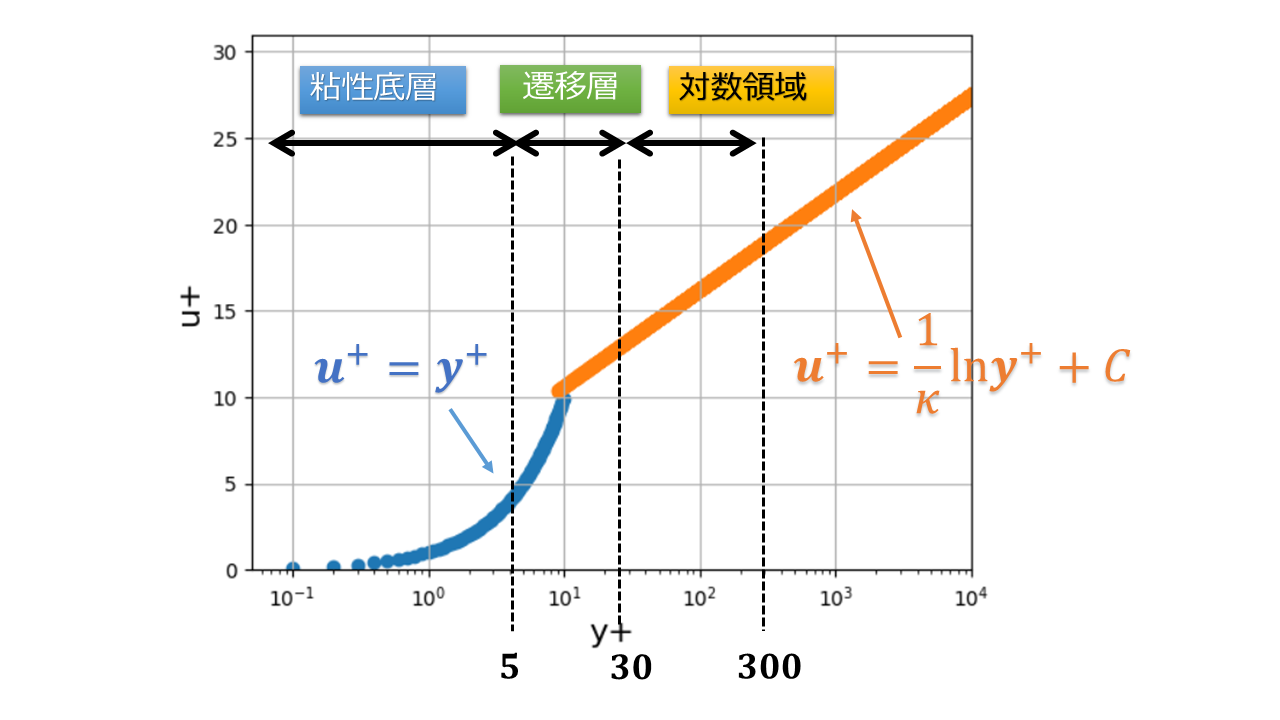
壁関数の速度分布
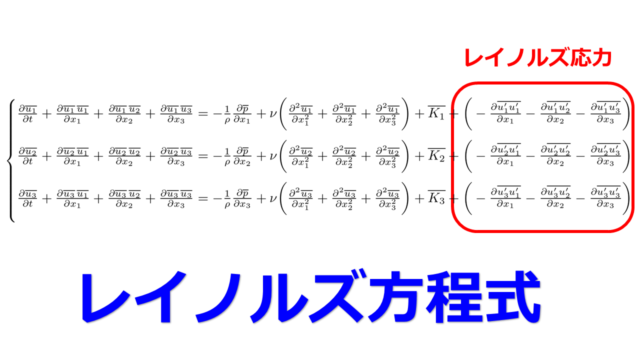
乱流状態では速度の乱れに応じたレイノルズ応力が発生するため、理論的に解析することが難しいのですが、実験結果に基づく経験的な解析によって壁近傍での乱流の速度分布を求めることができます。
平行平板の壁近傍の流れの漫画絵を描きました。
- 横軸:$x$方向
- 縦軸:$y$方向
壁と水平な方向($x$方向)の流速を$u$とします。
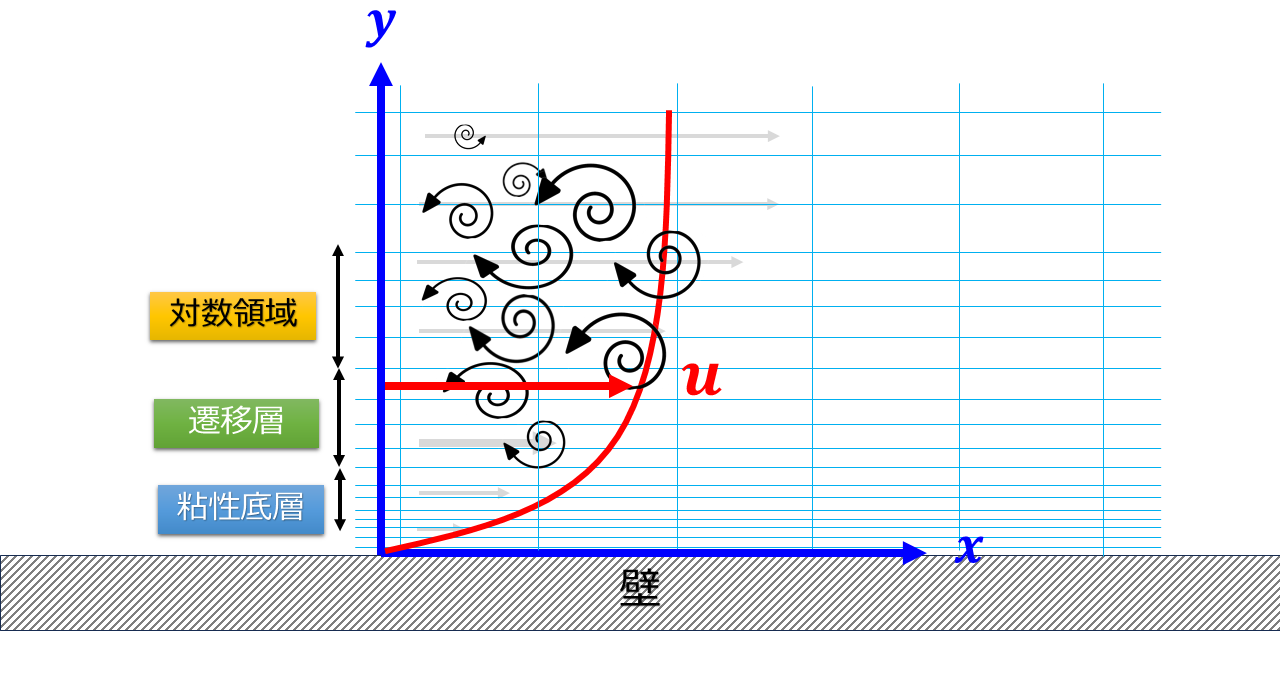
ただし、この分布の横軸と縦軸はそれぞれ以下のように壁近傍の特徴的な大きさで無次元化されていることに注意が必要です。
- $y^{+}=\frac{u_{\tau}y}{\nu}$
- $u^{+}=\frac{u}{u^{\tau}}$
※$u_{\tau}=\sqrt{\frac{\tau_{w}}{\rho}}$:摩擦速度
※$\tau_{w}=\mu\frac{\partial u}{\partial y}$:壁面のせん断力
※$\kappa=0.41, C = 5.0$
壁関数を使う理由
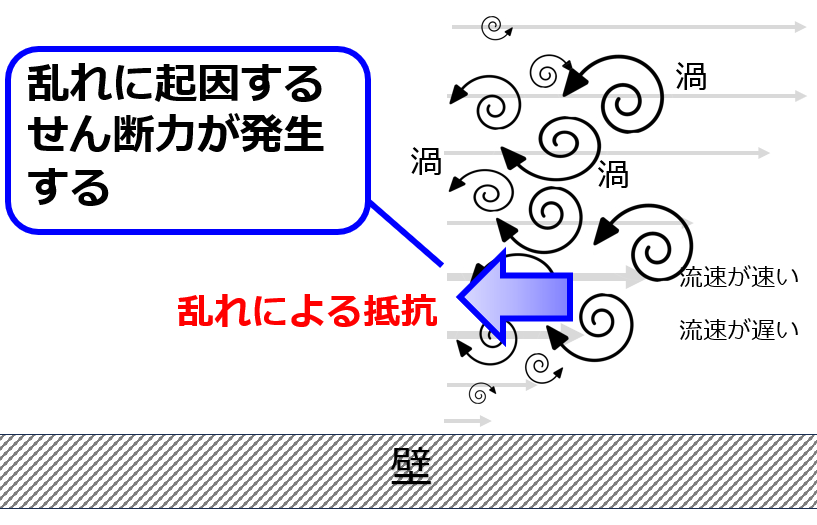
乱流状態での数値シミュレーションを行う際には大小様々なスケールの渦の解像度をとらえることが必要がでてきます。
なぜなら格子サイズより小さい渦は再現できず無視されてしまうからです。
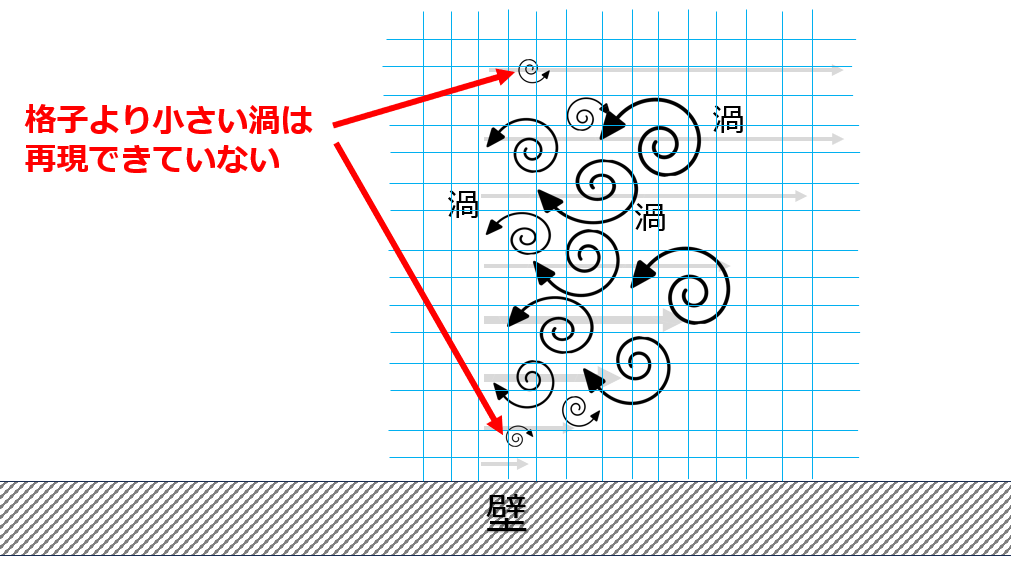
それが前回の記事の内容です。
つまり、通常の粘性抵抗(分子抵抗)と乱れによるせん断力(レイノルズ応力)を考えることで乱流状態を数理的に再現しようとするのがレイノルズ平均モデルです。
①流速差により生じるせん断力を分子粘性$\mu\frac{\partial u}{\partial y}$
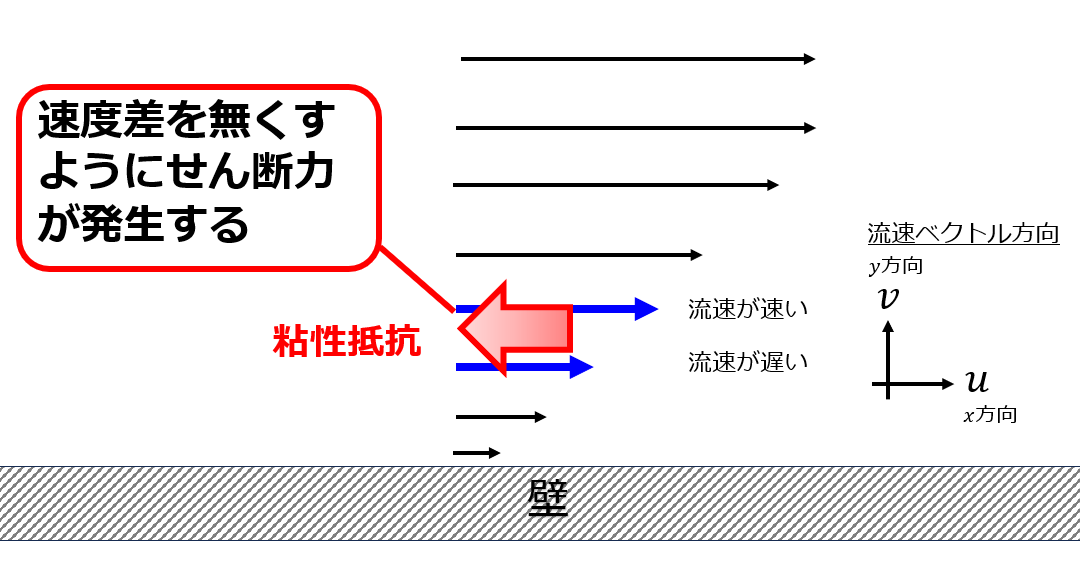
レイノルズ応力を導入したことにより、通常の速度差から生じるせん断力を区別するために分子粘性と呼ばれています。
壁近傍では以下のようにそれぞれのせん断力の大きさが変わります。
- 壁の極近傍では分子粘性がレイノルズ応力より著しく大きくなることから、乱れは小さくなります(層流的な流れ、低レイノルズ数)
- 壁から離れると乱流状態が著しくレイノルズ応力が大きくなります(乱流的な流れ、高レイノルズ数)

その際に対処する方法は以下の2つです。
今回は「②第一格子点を適切なサイズにして壁関数を用いる」の解説を行います。
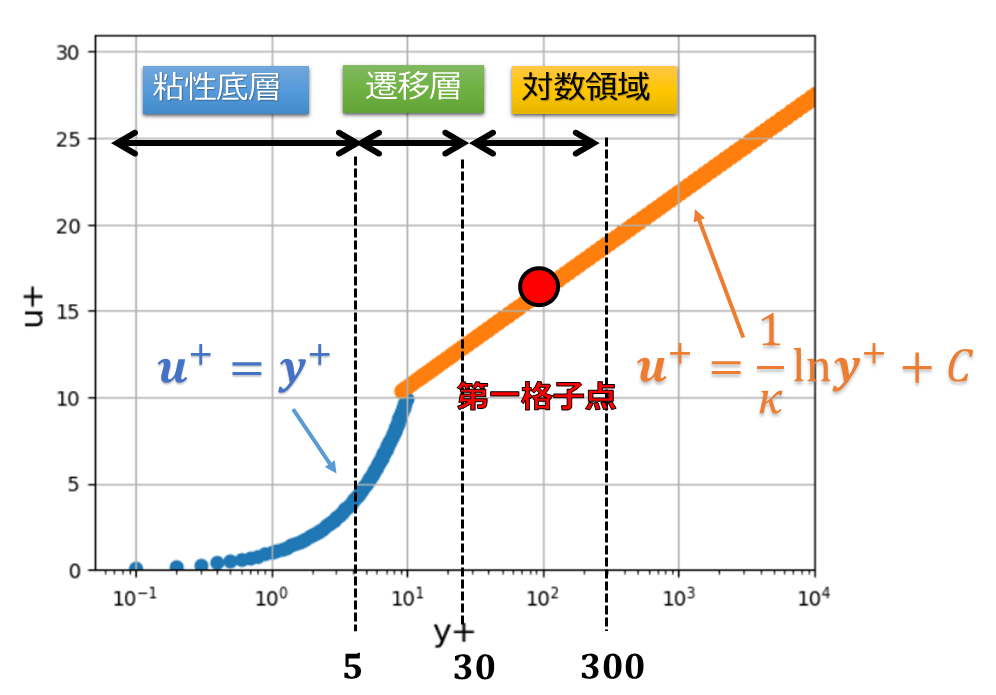
第一格子点を適切なサイズにして壁関数を用いる
境界条件として壁関数を使う際は壁近傍の格子サイズは細かくしすぎず第一層の格子点は対数領域になるように厚く設定をします。
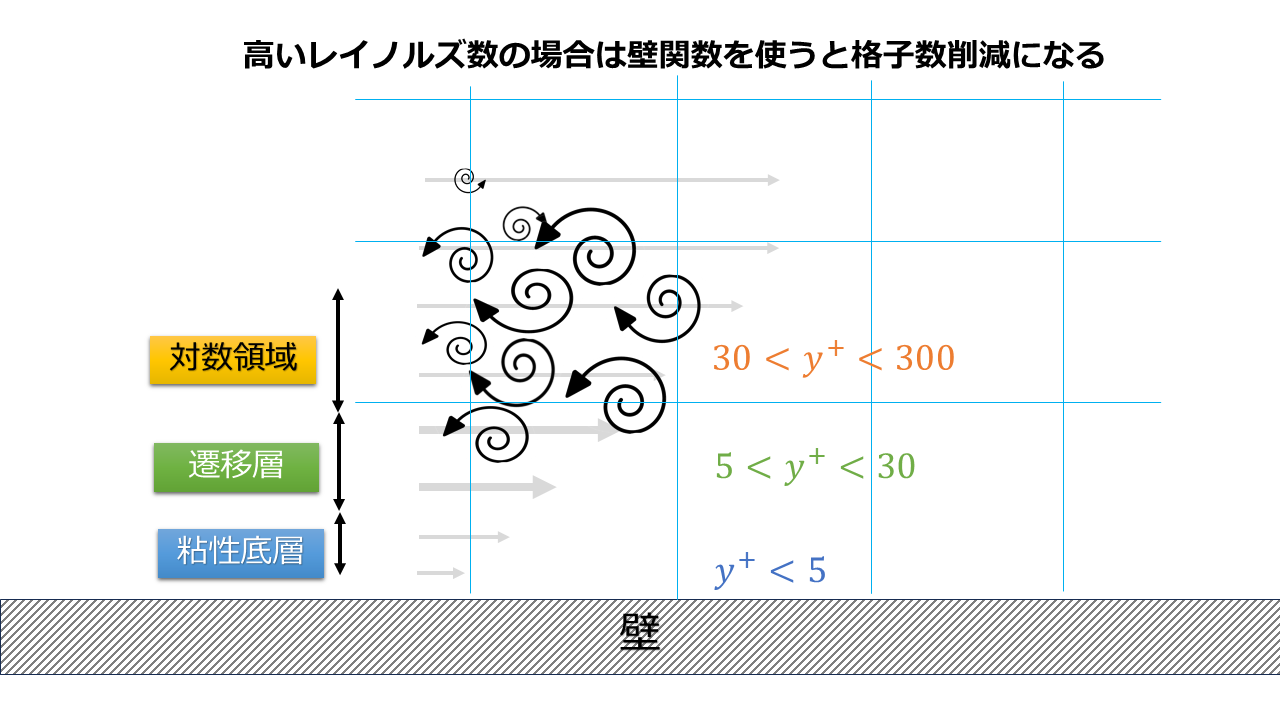
また、乱流状態での分子粘性よりレイノルズ応力が大きく高レイノルズ数の乱流状態の速度分布になっています。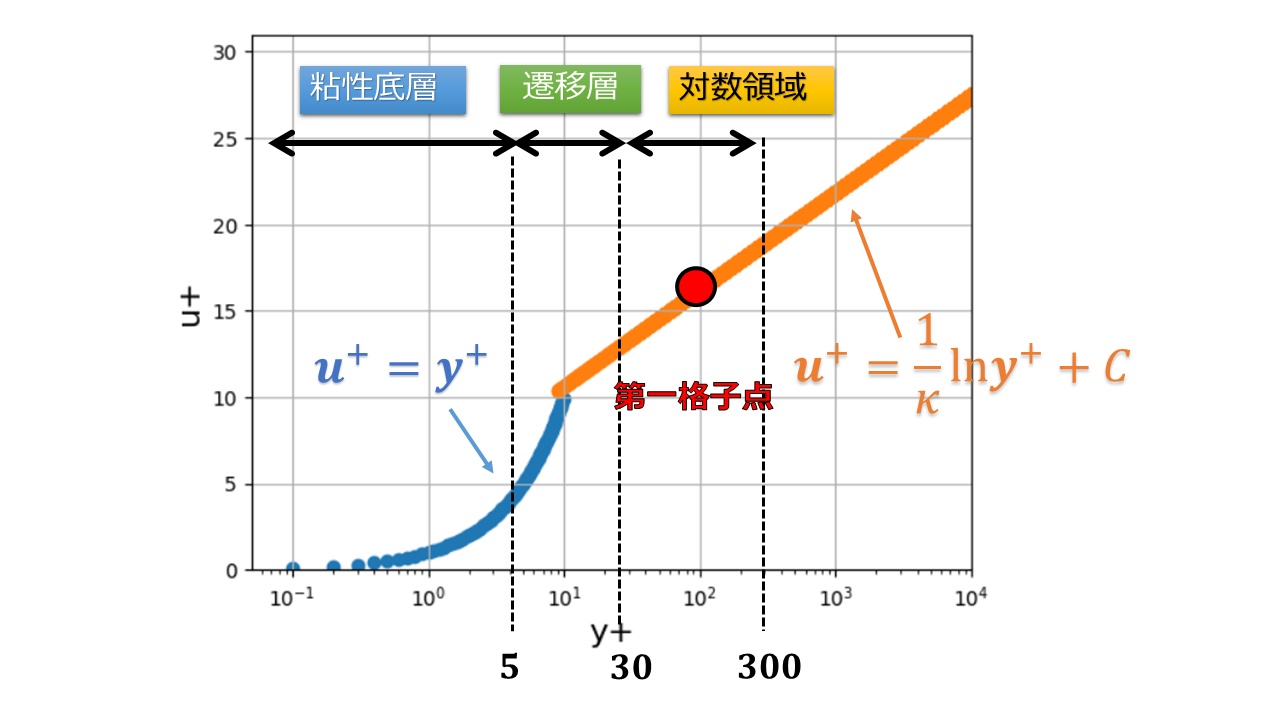
流体解析で「$y^{+}$の値がいくらなのか?」を確認するようにしましょう。
広い範囲の$y^{+}$に適用する乱流モデルや低レイノルズ型の乱流モデルも存在するため、必ずしもすべての乱流モデルで$y^+$が厳密に対数領域にある必要はありません。
壁関数における注意点
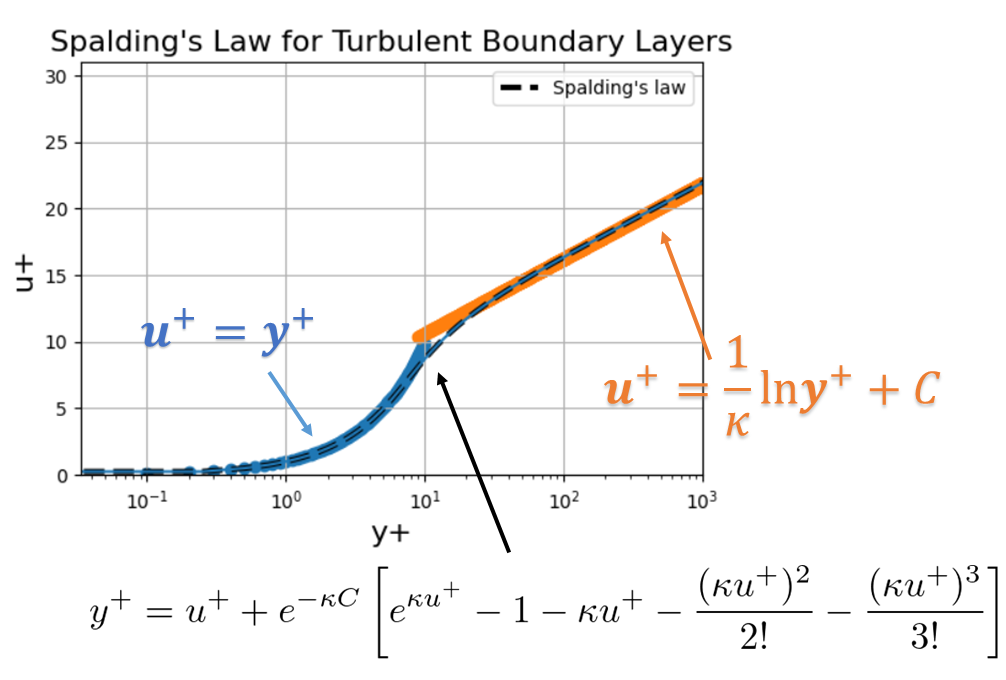
壁近傍で関数が
- $u^{+}=y^{+}$
- $u^{+}=\frac{1}{\kappa}\ln y^{+}+C$
に変わるのでそれを滑らかにつないだスパルディング則が提案されています。
y^+ = u^+ + e^{-\kappa C} \left[ e^{\kappa u^+} – 1 – \kappa u^+ – \frac{(\kappa u^+)^2}{2!} – \frac{(\kappa u^+)^3}{3!} \right]
\end{align*}
しかし、標準$k$-$\varepsilon$などの高レイノルズ型の乱流モデルを使う際は注意が必要です。
| 乱流モデル(高レイノルズ型) | |||
| 使う | 使わない | ||
| 壁関数 | 使う | ① | ② |
| 使わない | ③ | ④ | |
- 第一格子点が$y+$の大きい位置にくるように格子サイズを設定する($30<y^{+}<300$)
もし、第一格子点が$y^{+}<11$以下の場合、スパルディング則を適用していたとしても粘性低層や遷移層などの低レイノルズ数領域で乱流モデルが適切ではない - 乱流モデルを使わないのに壁関数を使うという状況はありえない。
- 壁面の境界条件に壁関数を使わないということであれば、格子サイズを十分小さくとって流束分布が滑らかになるようにしなくてはいけないが、壁面極近傍は低レイノルズ領域になるため高レイノルズ型の乱流モデルの前提条件が崩れてしまう
- 壁関数は使わず乱流モデルも使わないということであれば、壁面極近傍の流速分布を正確に解像できるだけの格子数を設け、なおかつ壁面から離れた領域の乱流状態の大小様々な渦サイズも解像できるだけ十分小さなサイズにする必要があり、とても現実的な計算規模になりえない。
高レイノルズ型の乱流モデルを使う場合に$30<y^{+}<300$に格子サイズを設定できない場合があると思います。
その場合は壁関数を用いる以外の対処方法が必要です。
例えば「①壁面近傍まで再現できる低レイノルズ型の乱流モデルを用いる」などで対処します。
などで対処します。
しかし、全ての状況にマッチする乱流モデルと壁関数は存在しないので、最後は実験や理論値と合っているかどうかを見極めて使うことになります。
まとめ
今回は平行平板の乱流の速度分布について解説しました。
高レイノルズ数の乱流モデルを使う際は「高レイノルズ数での流れ」という前提条件が崩れないように第一格子点は対数領域に来るように格子サイズを厚く設定することができます。
計算力学技術者のための問題アプリ
計算力学技術者熱流体2級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。
お勧めの参考書
乱流モデルの数式の展開が非常に丁寧なのはこちらの参考書です。
今まで読んだ本の中で途中式もしっかり書いてあって一番丁寧でした。
乱流モデルの話だけでなく、混相流(気液、固液)や粒子法、浅水方程式の話も乗っているので重宝しています。
乱流モデルはこちらもお勧めです。
前半は数値シミュレーションの離散化の話で、後半に乱流モデルの話が出てきます。
乱流モデルのざっくりした解説と流体全般の基礎知識にはこちらがちょうど良いでしょう。