こんにちは(@t_kun_kamakiri)
本日は「計算力学技術者試験の熱流体2級」で出てくるテーラー展開の解説をします。
テーラー展開は数値計算において微分を離散化する際には、必ず必要になってくる知識です。
理系学部の初学年の解析学で習うですが、社会人になって必ずしも皆が習っているわけではありませんので、これから計算力学技術者の熱流体を勉強する方を対象に問題を通して理解をしていければと思います。
- 計算力学技術者試験の熱流体2級を勉強している方
- テーラー展開は大学で習ったけど忘れてしまったのでサクッと復習したい方
※微分や偏微分などは理解している方を対象にしています。
では、問題です。
問題1の解説は本記事に書いていますが、問題2はご自身で解いてください。
解答はまとめに書いています。
テーラー展開
$x=a$のまわりでの関数の形を知りたい場合、テーラー展開を使います。
テーラー展開は以下の自身の関数の微分を使って、1次曲線、2次曲線、3次曲線・・・など多項式で表現したものです。
と書くことができます。
Σの和があるとわかりにくいですが、展開しておくと多項式近似であることがわかります。
&+\frac{f^{(2)}(x)}{2!}|_{x=a}(x-a)^{2}\\
&+\cdot\cdot\cdot+\frac{f^{(n)}(x)}{n!}_{x=a}(x-a)^{n}+\\
&\cdot\cdot\cdot\end{align*}
※\(f^{(n)}(x)=\frac{d^{n}f(x)}{dx^{n}}\):n階微分
念のため注意ですが$\frac{f^{(1)}(x)}{1!}|_{x=a}$は$x$で微分してから$x=a$を代入するって意味です。
$x=a$を代入してから微分してはいけませんよ(0にしかなりませんから)。
テーラー展開の次数
テーラー展開した際に何次の項まで残すかによって、数値的な離散化の精度を表すことがあります。
数値計算をやったことがない人には馴染みがないかもしれませんので、差分法についての詳しい話は後回しにしても良いです。
話題に上がった時に解説しましょう。
とにかく、今はテーラー展開したの際の各項を以下のように呼ぶということを覚えておきましょう。

問題であったような「3次の項まで残す」という意味がここで分かってくるでしょう。
そうです。上の式の3次の項まで残して計算するのです。
つまり、「3次の項まで残す」とはこういうことです。
f(x)=f(a)+\frac{f^{(1)}(x)}{1!}|_{x=a}(x-a)+\frac{f^{(2)}(x)}{2!}|_{x=a}(x-a)^{2}+\frac{f^{(3)}(x)}{3!}|_{x=a}(x-a)^{3}
\end{align*}
「\(f^{(n)}(x)=\frac{d^{n}f(x)}{dx^{n}}\):n階微分」の表記が慣れない人は、こうなっていると見てください。
f(x)=f(a)+\frac{1}{1!}\frac{df}{dx}|_{x=a}(x-a)+\frac{1}{2!}\frac{d^2f}{dx^2}|_{x=a}(x-a)^{2}+\frac{1}{3!}\frac{d^3f}{dx^3}|_{x=a}(x-a)^{3}
\end{align*}
少し、複雑に見えるかもしれませんがこれくらいの計算なら微分を丁寧に行えば問題なさそうです。
マクローリン展開
任意の$x=a$近傍での展開はテーラー展開と呼びますが、$x=0$近傍での展開を特にマクローリン展開と呼びます。
例えば「3次の項までマクローリン展開しなさい」と問われたら、以下のようにします。
f(x)=f(0)+\frac{1}{1!}\frac{df}{dx}|_{x=0}x+\frac{1}{2!}\frac{d^2f}{dx^2}|_{x=0}x^{2}+\frac{1}{3!}\frac{d^3f}{dx^3}|_{x=0}x^{3}
\end{align*}
マクローリン展開しなさいということなので、$x=0$の近傍で展開するということです。
わざわざ「$x=0$近傍でマクローリン展開をしなさい」と書かれないので注意が必要です。
問題1の解説
「$x=0$のまわりで」と書いているので、マクローリン展開自体が$x=0$のまわりで展開することなので、「$x=0$のまわりで」と表記されていない場合もあります。
「3次の項までマクローリン展開」は、以下のようにします。
f(x)=f(0)+\frac{1}{1!}\frac{df}{dx}|_{x=0}x+\frac{1}{2!}\frac{d^2f}{dx^2}|_{x=0}x^{2}+\frac{1}{3!}\frac{d^3f}{dx^3}|_{x=0}x^{3}\tag{1}
\end{align*}
ここで、$f(x)=\sin x$と考えれば良いです。
テーラー展開やマクローリン展開は、大学の解析学など1年生の段階で習うものですが、初めて見る人にとっては少々インパクトのある難しいイメージを持ちますが、(1)を見てわかる通りひたすら微分すればいいだけです。
では、微分してみます。
- $f(x)=\sin x$
- 1階微分:$\frac{df}{dx}=\cos x$
- 2階微分:$\frac{d^2f}{dx^2}=-\sin x$
- 3階微分:$\frac{d^3f}{dx^3}=-\cos x$
この結果に対して$x=0$を代入していきます。
- $f(0)=0$
- $\frac{df}{dx}|_{x=0}=1$
- $\frac{d^2f}{dx^2}|_{x=0}=0$
- $\frac{d^3f}{dx^3}|_{x=0}x^{3}=-1$
(1)に代入します。
もしくは、「3!=6」なので
f(x)=x-\frac{1}{6}x^{3}
\end{align*}
でも良いです。
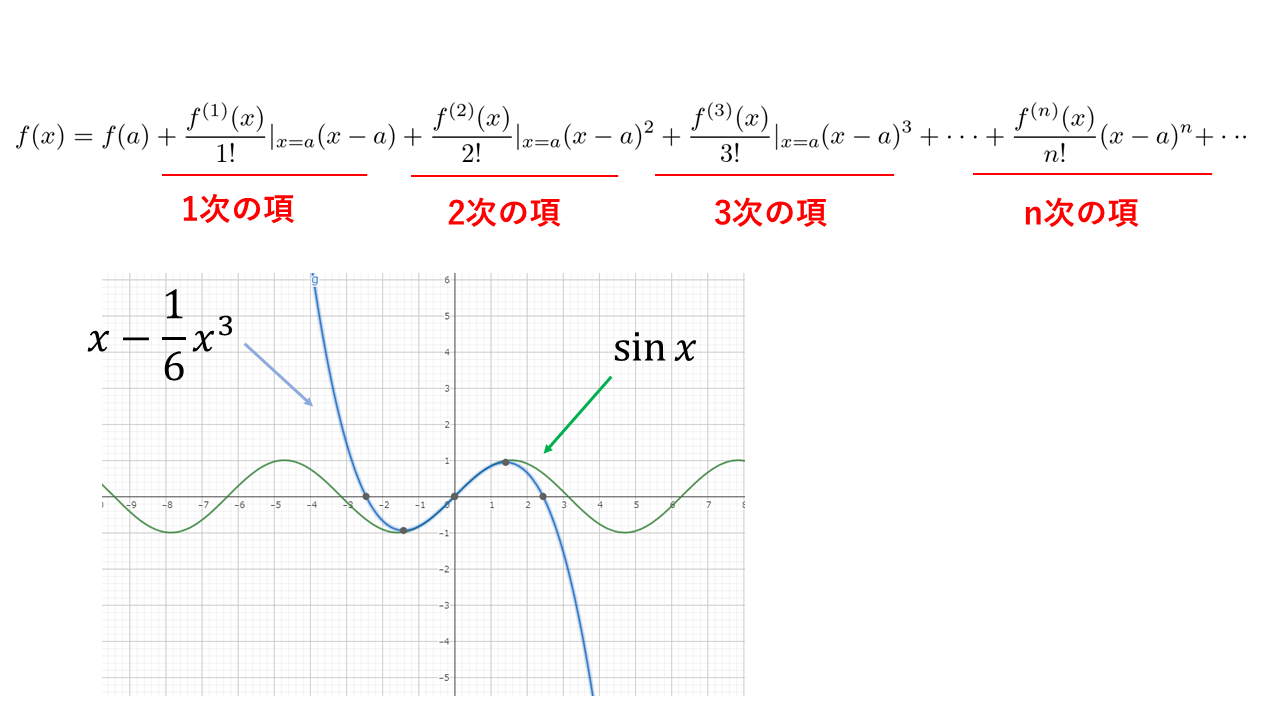
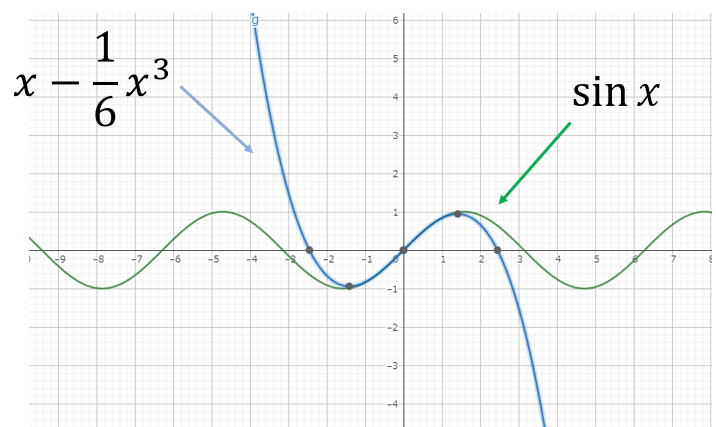
$\sin x$を$x=0$のまわりで上式のように3次の項までテーラー展開(マクローリン展開)したものを描写してみました。
$x=0$の近傍では良い近似になっているのがわかります。
まとめ
テーラー展開の計算には
- テーラー展開の定義を覚える
- 何次の項まで残すか決める
- $f(x)$の微分をひたすら行う
- $f(x)$の微分をした後で$x=a$を代入
計算力学技術者のための問題アプリ
計算力学技術者熱流体2級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。
お勧めの参考書
テーラー展開は解析学で学ぶことができます。