流体力学の基礎方程式のひとつとして運動量保存則があります。
それは、こんな感じ。

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (1)\end{align*}

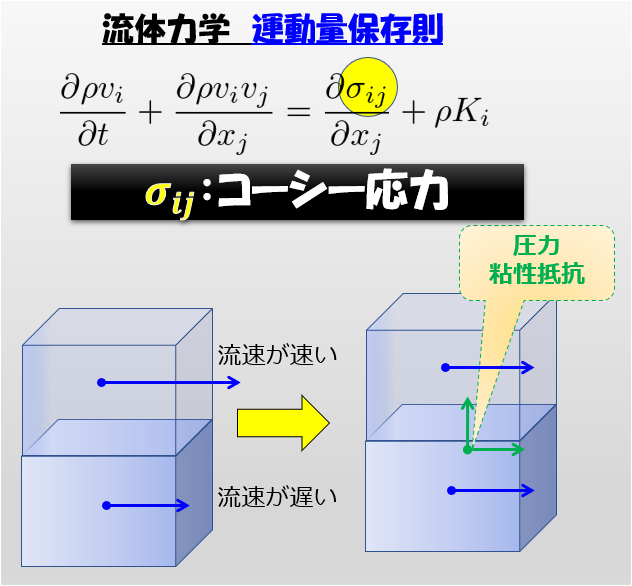
右辺第一項に着目したとき、\(\sigma_{ij}\)は何か？

これは、流体要素間にはたらく応力を意味しています。

この応力をコーシー応力と呼びます。

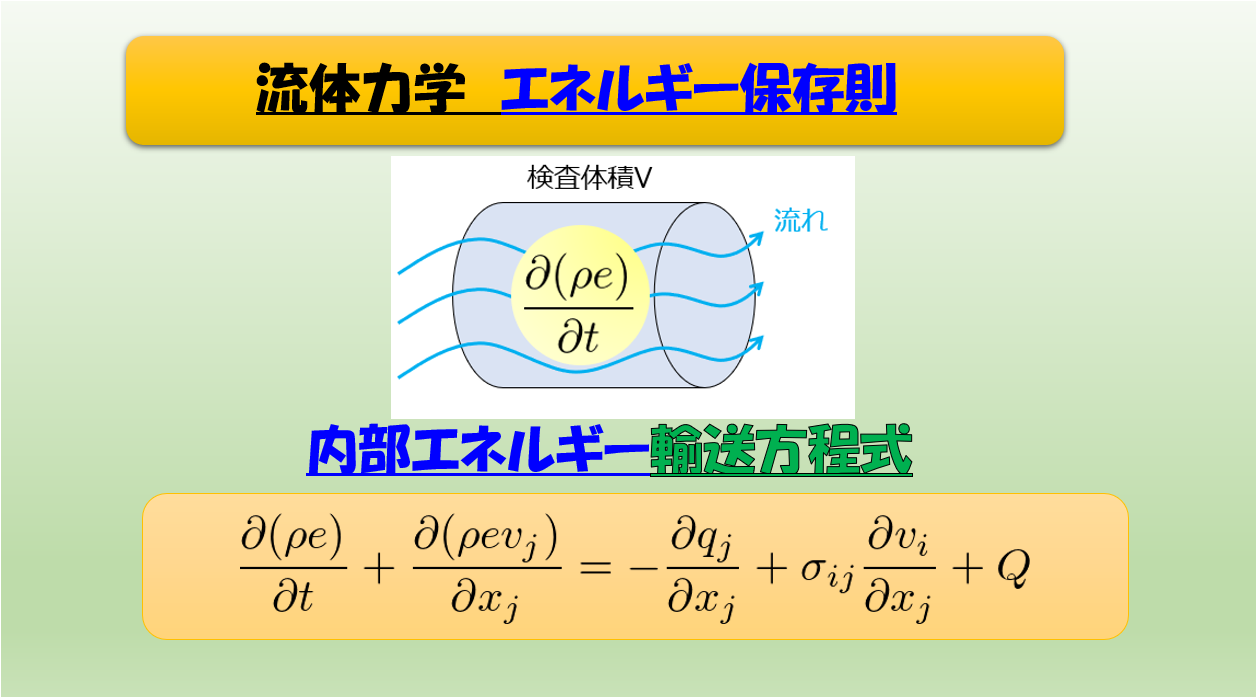
下記のような、流体力学のナビエストークス方程式を見ると、

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=-\frac{\partial p}{\partial x_{i}}+\mu\frac{\partial^2 v_{i}}{\partial x_{j}^2}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

このように、右辺に圧力項と粘性項がありますよね。

  • 圧力項：\(-\frac{\partial p}{\partial x_{i}}\)
  • 粘性項：\(\mu\frac{\partial^2 v_{i}}{\partial x_{j}^2}\)

コーシー応力は、この圧力と粘性抵抗に関係した応力であります。

本記事の内容

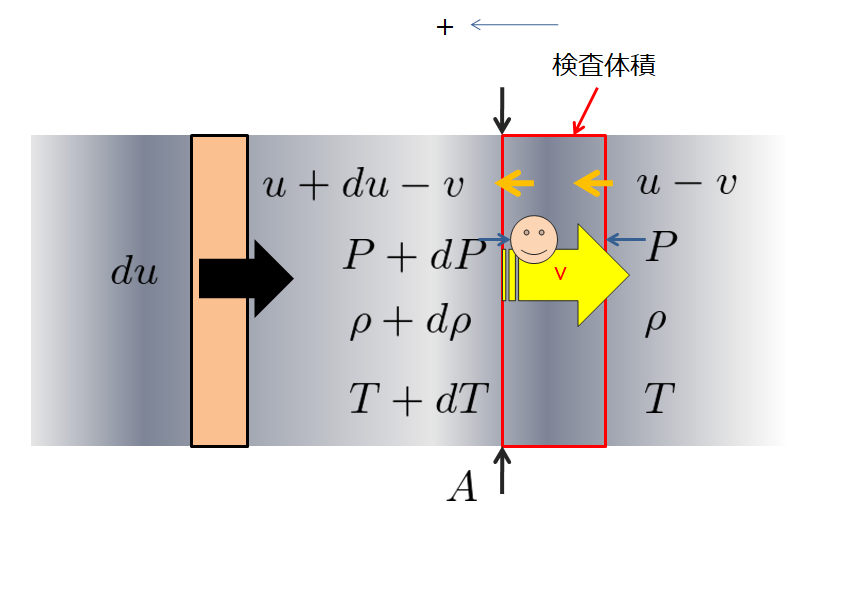
流体力学での圧力と粘性を図で示す。

スポンサーリンク

目次
  1. 圧力と粘性抵抗
    1. 圧力
    2. 粘性抵抗
  2. コーシー応力をまとめると
  3. まとめ

圧力と粘性抵抗

コーシー応力が圧力と粘性抵抗に関係する応力であることを前段で触れましたので、流体における圧力と粘性について図で説明したいと思います。

それには下記のような流体領域を考え、流体要素に分割することを考えます。

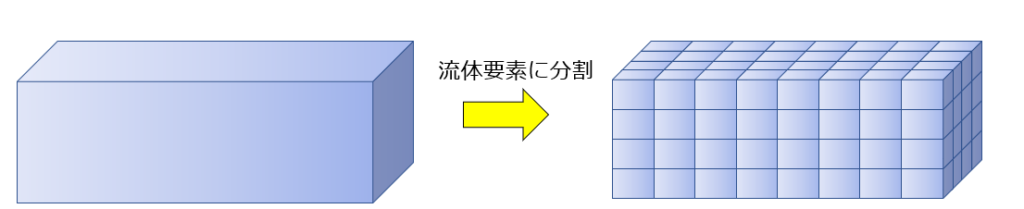
流体現象をどのように数式で記述しようかと考えた時に、粒子が十分つまっているくらいの要素に細かく分割するのですよね。

これを連続体近似といいます。

あわせて読みたい

連続体かどうかの判断：クヌッセン数（クヌーセン数）

圧力

流体要素に分割したときに、たとえ流れがなくても要素間には垂直応力がはたらきます。

これが圧力に値する力です。

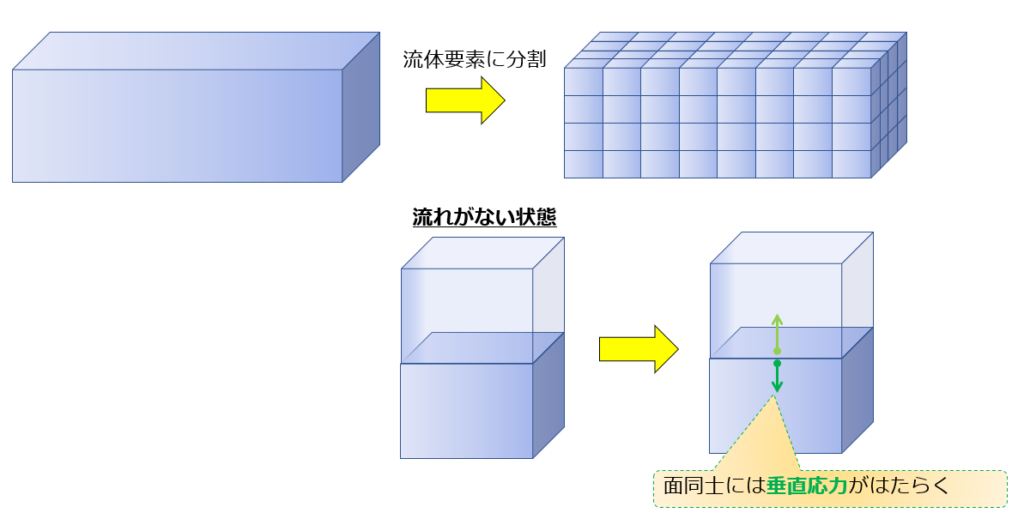
※流れがない場合に圧力がはたらくという意味ではなく、流れがあってもなくても要素間は常に圧力を持っていますという意味です。

流体要素間の速度差がない場合にはたらく力が圧力ということです。

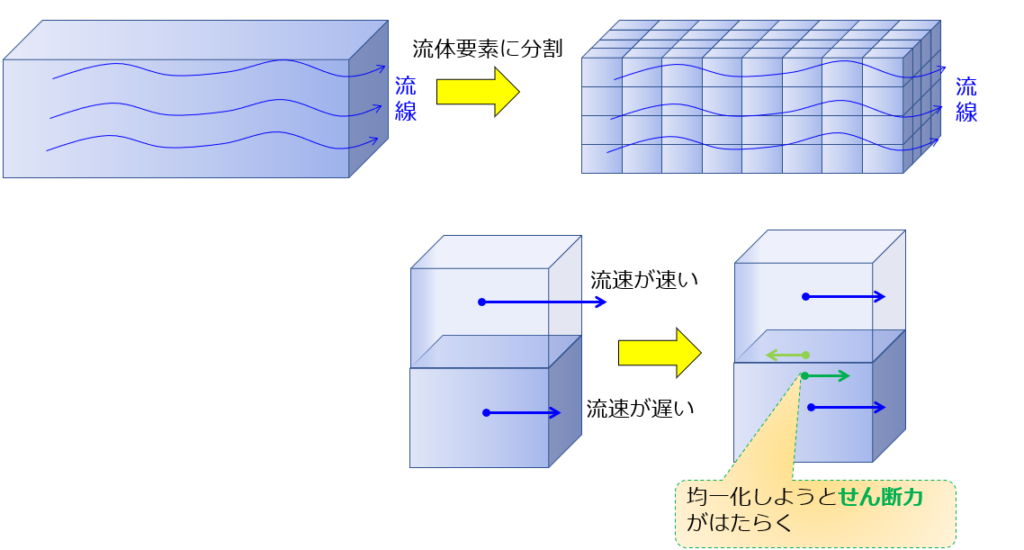
粘性抵抗

今度は流れがある状態を考えます。

いま、流体要素間は異なる流速を持っているものとします。

そういった状況下では、流体要素間には流れを均一化しようとする方向にせん断力がはたらきます。

流速が速い部分は遅くなろうとし、流速が遅い部分は速くなろうとします（散逸がなければ・・・）。

これが粘性抵抗に値する力です。

あるいは・・・

要素間の面に対して垂直な方向の異なる流速がある場合にも、流れを均一化させる方向に垂直応力がはたらきます。

これも粘性抵抗に値する力です。

遅い流れがあると「もたもたするな」と隣の要素が引っ張ってくれるとイメージしましょう。

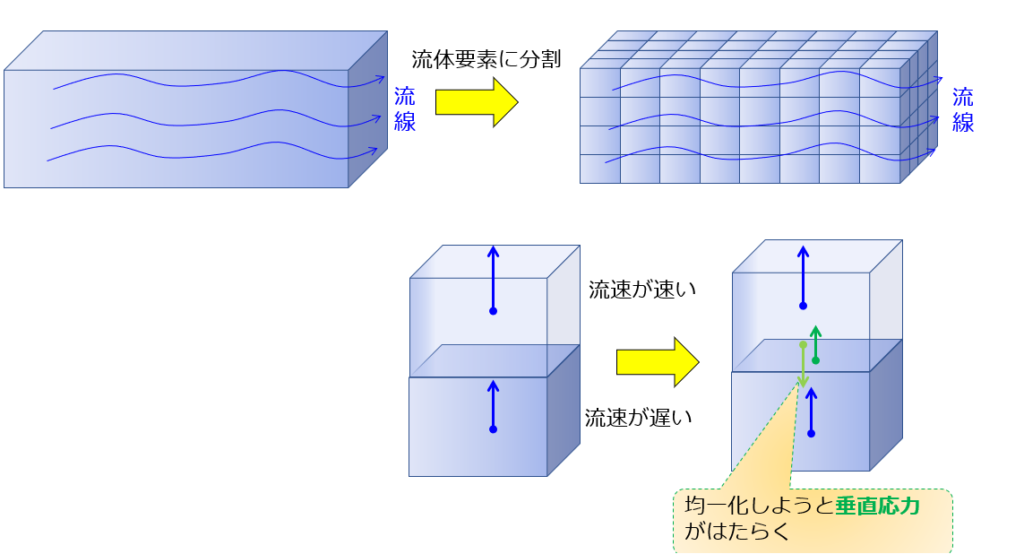
流体要素間の速度差がある場合にはたらく力が粘性抵抗ということです。

コーシー応力をまとめると

コーシー応力\(\sigma_{ij}\)は次の2つの力に分類できます。

  • 圧力：流体要素間の速度差がない場合にはたらく力
  • 粘性抵抗：流体要素間の速度差がある場合にはたらく力

まとめ

運動量保存則
\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (1)\end{align*}

流体力学の運動量保存則の、\(\sigma_{ij}\)（コーシー応力）について説明しました。

別の記事で、コーシー応力\(\sigma_{ij}\)の具体的な形を導出したいと思います。

流体力学の基本的な変数は、「流速\(\boldsymbol{v}\)、圧力\(p\)、温度\(T\)、密度\(\rho\)」だから、\(\sigma_{ij}\)（コーシー応力）もこれらの基本的な変数で記述することが目標になります。

ただ、式で導出しようと思うとその過程は結構煩雑になるので頑張って導出してみてください。