【OpenFOAM】ケルビンヘルムホルツ不安定性の流体解析

本記事の目標

OpenFOAMを使って、ケルビンヘルムホルツ不安定性の解析計算を行う。

ケルビンヘルムホルツ不安定性に興味を持って、OpenFOAMでできるかなって思ってやってみただけですので、特にメッシュの切り方やパラメータや方程式の解き方（離散化）などはこだわってやっていません。

研究に使うとか仕事に使うとかではありませんので、遊び感覚でできました。

※注意
本記事は、OpenFOAM を使用していますがはじめてOpenFOAMを触る人向けには書いていません。

設定ファイルは下記から入手できます。
casefile

でもOpenFOAMを触ったことがあって、使い方はちょっとは知っているよって人は上記のファイルを入手して下記のコマンドを打てば「メッシュ作成」から「解析実行」までできると思います。

#コマンド実行
blockMesh
setFields
decomposePar
mpirun -np 2 interFoam -parallel >log &
・・・・
・・・・
計算が終わったら・・・
reconstructPar

#コマンド実行

blockMesh

setFields

decomposePar

mpirun -np 2 interFoam -parallel >log &

・・・・

計算が終わったら・・・

reconstructPar

ケルビンヘルムホルツとは
1. 概要
2. 実現象での例
CAE解析
解析結果
感想
おまけ

ケルビンヘルムホルツとは

概要

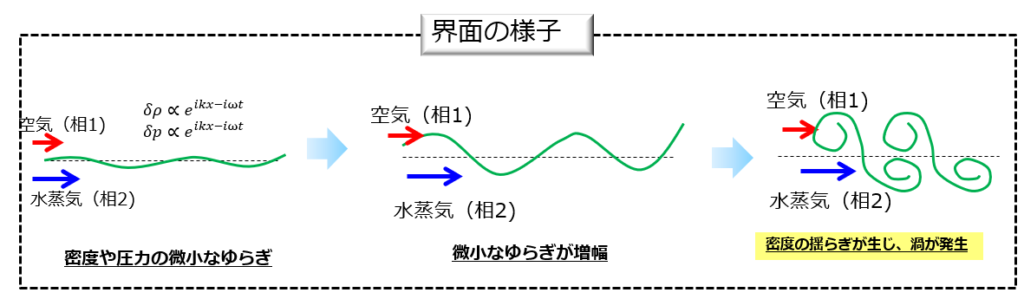
異なる速度（密度）をもつ2相の間で起こる不安定性現象です。

2相の界面でせん断力があるため不安定性の種（渦）が生じ、それが時間とともに増幅することで生じる2次元的な模様のことを指します。

実現象での例

ケルビンヘルムホルツ不安定性は、こんな感じ。

飛行機の窓から外を眺めているとたまに見かける渦を巻いた雲や、木星の模様もケルビンヘルムホルツ不安定性の現象が作り出した模様です。

CAE解析

OpenFOAMの2相流のソルバ”interFoam”を用いてケルビンヘルムホルツ不安定性を再現したいと思います。

ツール

OpenFOAM:ver4.x
ソルバ：inerFoam

解くべき方程式

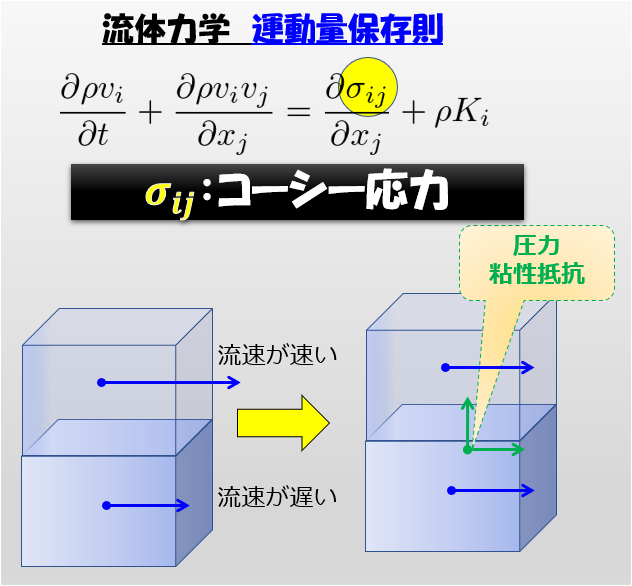
運動方程式（2次元）
体積分率の保存
表面張力
※VOFによる界面の表現

今回使っている「interFoam」のソルバはVolume Of Fluid(VOF)法による、二相流ソルバーです。

相の区別を各相の体積分率(0~1)で行い、密度や粘性を体積分率をかけて、ナビエストークス方程式を解いています。

ナビエストークス方程式

\begin{align*}\frac{\partial \rho_{b}\boldsymbol{u}}{\partial t}+\nabla\cdot\big(\rho_{b}\boldsymbol{u}\boldsymbol{u}\big)=-\nabla p+\nabla\cdot\mu_{b}\big(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{T}\big)+\rho_{b}\boldsymbol{f}+\boldsymbol{F}_{s}\end{align*}

密度

\begin{align*}\rho_{b}=\alpha_{1}\rho_{1}+\alpha_{2}\rho_{2}\end{align*}

粘性

\begin{align*}\mu_{b}=\alpha_{1}\mu_{1}+\alpha_{2}\mu_{2}\end{align*}

表面張力

\begin{align*}\boldsymbol{F}_{s}=\gamma \kappa\big(\nabla \alpha\big)\end{align*}

\begin{align*}\kappa=\nabla\cdot\big(\frac{\nabla\alpha}{|\nabla\alpha|}\big)\end{align*}

非圧縮の条件

\begin{align*}\nabla\cdot \boldsymbol{u}=0\end{align*}

体積分率の移流方程式

\begin{align*}\frac{\partial \alpha}{\partial t}+\nabla\cdot \big(\alpha \boldsymbol{u}\big)=0\end{align*}

※\(\alpha_{2}=1-\alpha_{2}\)

※\(\kappa\)：界面の曲率

※\(\gamma\)：界面張力

境界条件と解析領域

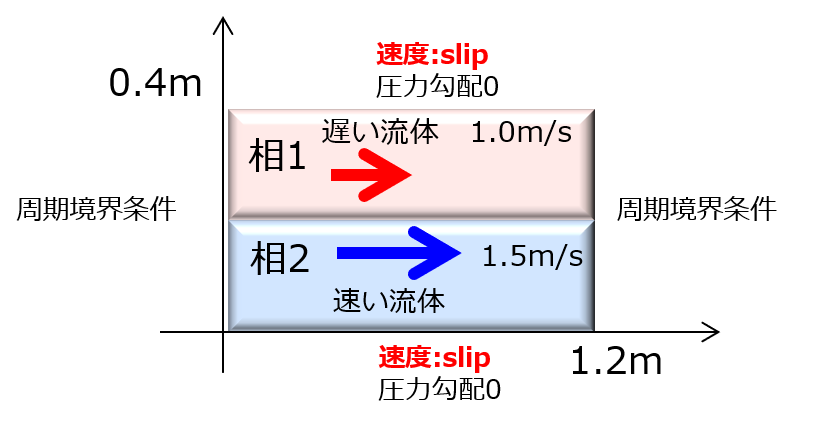
その他

2次元解析
乱流モデル無し
非定常計算
時間間隔：クーラン数1

メッシュ作成

メッシュ作成はOpenFOAMのユーティリティにあるblockMeshのみで作成しています。

設定方法：blockMeshDict

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  4.x                                   |
|   \\  /    A nd           | Web:      www.OpenFOAM.org                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    object      blockMeshDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

convertToMeters 0.001;

vertices
(
    (0 0 0) //0
    (1200 0 0) //1
    (1200 120 0)//2
    (1200 200 0)//3
    (1200 280 0)//4
    (1200 400 0)//5
    (0 400 0)//6
    (0 280 0)//7
    (0 200 0)//8
    (0 120 0)//9
    (0 0 1) //10
    (1200 0 1) //11
    (1200 120 1)//12
    (1200 200 1)//13
    (1200 280 1)//14
    (1200 400 1)//15
    (0 400 1)//16
    (0 280 1)//17
    (0 200 1)//18
    (0 120 1)//19
);

blocks
(
    hex (0 1 2 9 10 11 12 19) (600 60 1) simpleGrading (1 1 1)
    hex (9 2 3 8 19 12 13 18) (600 60 1) simpleGrading (1 1 1)
    hex (8 3 4 7 18 13 14 17) (600 60 1) simpleGrading (1 1 1)
    hex (7 4 5 6 17 14 15 16) (600 60 1) simpleGrading (1 1 1)
);

edges
(
);

boundary
(
    leftWall
    {
        type cyclic;
        neighbourPatch rightWall;
        faces
        (
            (0 10 19 9)
            (8 9 19 18)
            (7 8 18 17)
            (6 7 17 16)
        );
    }
    rightWall
    {
        type cyclic;
        neighbourPatch leftWall;
        faces
        (
            (1 2 12 11)
            (2 3 13 12)
            (3 4 14 13)
            (4 5 15 14)
        );
    }

    lowerWall
    {
        type empty;
        faces
        (
            (0 1 2 9)
            (9 2 3 8)
            (8 3 4 7)
            (7 4 5 6)
        );
    }

    topWall
    {
        type empty;
        faces
        (
            (10 11 12 19)
            (19 12 13 18)
            (18 13 14 17)
            (17 14 15 16)
        );
    }
    FrontWall
    {
        type wall;
        type  zeroGradient;
        faces
        (
            (0 1 11 10)
        );
    }
    BackWall
    {
        type wall;
        //type zeroGradient;
        faces
        (
            (6 5 15 16)
        );
    }


);

mergePatchPairs
(
);

// ************************************************************************* //

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

/*--------------------------------*- C++ -*----------------------------------*\

| ========= | |

| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |

| \\ / O peration | Version: 4.x |

| \\ / A nd | Web: www.OpenFOAM.org |

| \\/ M anipulation | |

\*---------------------------------------------------------------------------*/

FoamFile

{

version 2.0;

format ascii;

class dictionary;

object blockMeshDict;

}

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

convertToMeters 0.001;

vertices

(

(0 0 0) //0

(1200 0 0) //1

(1200 120 0)//2

(1200 200 0)//3

(1200 280 0)//4

(1200 400 0)//5

(0 400 0)//6

(0 280 0)//7

(0 200 0)//8

(0 120 0)//9

(0 0 1) //10

(1200 0 1) //11

(1200 120 1)//12

(1200 200 1)//13

(1200 280 1)//14

(1200 400 1)//15

(0 400 1)//16

(0 280 1)//17

(0 200 1)//18

(0 120 1)//19

);

blocks

(

hex (0 1 2 9 10 11 12 19) (600 60 1) simpleGrading (1 1 1)

hex (9 2 3 8 19 12 13 18) (600 60 1) simpleGrading (1 1 1)

hex (8 3 4 7 18 13 14 17) (600 60 1) simpleGrading (1 1 1)

hex (7 4 5 6 17 14 15 16) (600 60 1) simpleGrading (1 1 1)

);

edges

(

);

boundary

(

leftWall

{

type cyclic;

neighbourPatch rightWall;

faces

(

(0 10 19 9)

(8 9 19 18)

(7 8 18 17)

(6 7 17 16)

);

}

rightWall

{

type cyclic;

neighbourPatch leftWall;

faces

(

(1 2 12 11)

(2 3 13 12)

(3 4 14 13)

(4 5 15 14)

);

}

lowerWall

{

type empty;

faces

(

(0 1 2 9)

(9 2 3 8)

(8 3 4 7)

(7 4 5 6)

);

}

topWall

{

type empty;

faces

(

(10 11 12 19)

(19 12 13 18)

(18 13 14 17)

(17 14 15 16)

);

}

FrontWall

{

type wall;

type zeroGradient;

faces

(

(0 1 11 10)

);

}

BackWall

{

type wall;

//type zeroGradient;

faces

(

(6 5 15 16)

);

}

);

mergePatchPairs

(

);

// ************************************************************************* //

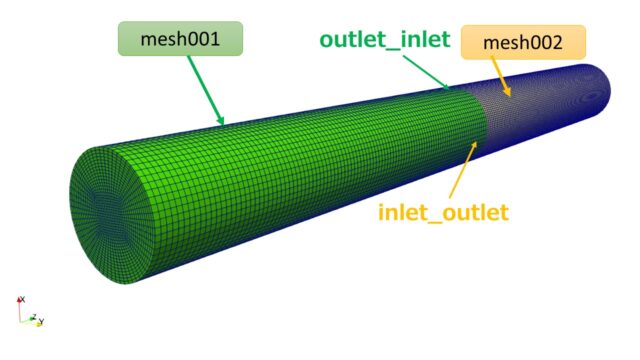
ざっくりこんな感じで切ってみました。

界面のまわりだけちょっとだけメッシュを細かくしています。

どれくらい細かくすれば良いかは、わからないのでメッシュサイズにこだわり過ぎず、まずは荒くメッシュを切って計算がうまくいっていることを確認してからメッシュサイズを見直しても良いかもしれません。

初期状態の設定

初期状態の設定は、setFiledsを使います。

設定方法：setFiedDict

/*--------------------------------*- C++ -*----------------------------------*\
| =========                 |                                                 |
| \\      /  F ield         | OpenFOAM: The Open Source CFD Toolbox           |
|  \\    /   O peration     | Version:  4.x                                   |
|   \\  /    A nd           | Web:      www.OpenFOAM.org                      |
|    \\/     M anipulation  |                                                 |
\*---------------------------------------------------------------------------*/
FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      setFieldsDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //


defaultFieldValues
        (
            volScalarFieldValue alpha.water 0
            volVectorFieldValue U (1.0 0 0)    
        );

regions
(
    boxToCell
    {
        box (0 0 0) (1.2 0.2 0.1);
        fieldValues
        (
            volScalarFieldValue alpha.water 1
            volVectorFieldValue U (1.5 0 0)    
        );
    }
);

// ************************************************************************* //