どうも(^^)
前回の続きになりますが、前回の記事では流体解析には流れの性質をよく理解しておく必要があることを述べました。
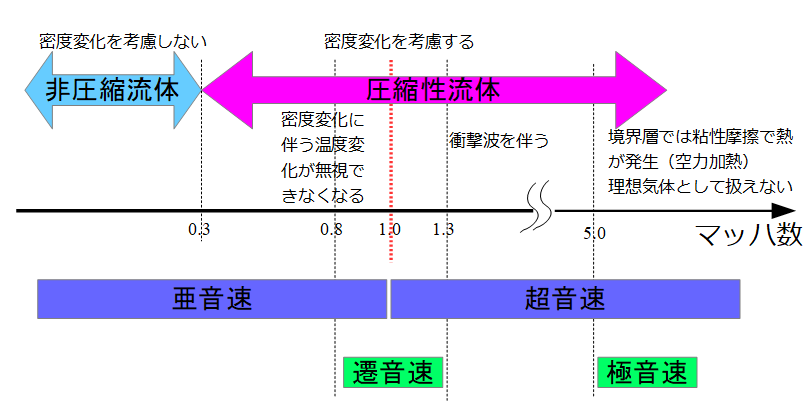
特に、流体解析において「非圧縮性流体」「圧縮性流体」に区別は特に重要であり、両者の区別はマッハ数がとても重要なパラメータになることを示しました。
マッハ数\(M=\frac{u}{a}\)
※\(a\):音速、\(u\):代表の流速
マッハ数はこんな感じで書けるのですが、分母に音速\(a\)というのがあります。
この時点では、音速\(a\)が何者かわかりませんよね(笑)
でもこの音速\(a\)が「非圧縮性流体」「圧縮性流体」の判別にとても重要な物理量なのですが、なぜ重要なのかを本記事で示したいと思います。
本記事の目標
「非圧縮性流体」「圧縮性流体」の判別に音速が重要であることを示す。
理解したい内容をもう一度整理しておくと、
- 非圧縮性流体・圧縮性の判別をしたい
↓
- 密度変化が無視できるかどうかを見積もれば良い
↓
- マッハ数が見積もりに使われるようだ
↓
- 流速と音速の大小が重要である:本記事の内容
このフローを逆に辿って理解していけば、非圧縮性流体・圧縮性流体の判別を理解できます。(少しづつ投稿していきます。)
密度波
非圧縮性流体と考えれるかどうかは、密度の変化を考慮するかどうかを考えれば良いわけですよね。
ということは、流体における密度伝搬がどういった速度で伝わっているかを考えれば良いということになります。
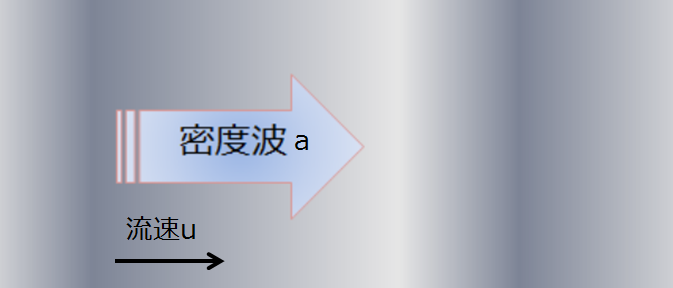
イメージ
y
↑→x
イメージはこんな感じでしょうか。
密度が疎密波で伝搬する(密度波)といった感じです。
そこを流体が流速\(u\)で流れているというイメージです。
流体力学の基礎方程式は、基本的には流速\(u\)を求めるためのものです。
ですので、この密度波が考慮した方が良いのかどうかというのは、「密度伝搬の速度」と「流速」の大小を比較することに他なりません。
この密度伝搬の速度のことを音速と言います。
| 非圧縮性流体 | 密度伝搬が無視できる\(a>>u\) |
| 圧縮性流体 | 密度伝搬が無視できない\(a\simeq u\) |
密度伝搬の速度と流速が同程度なら密度変化を考慮しなくはいけないということになりますね(^^)
この密度伝搬の速度を見積れば良いということになりますので、早速やってみましょう(^^)/
密度伝搬の速度:微小じょう乱
非圧縮性流体の基礎方程式:1次元
簡単のために一次元で考えましょう(^^)
粘性も熱拡散も無視します。(\(\nu=0,\alpha=0\))
※粘性は流速の垂直方向の速度勾配(\(\nu=\mu/\rho=\frac{1}{\rho}\frac{\partial u(x)}{\partial y}\))があるときに重要なので一様な流れを考えている場合は考慮しなくても良いでしょう。
温度に関しても温度を一様としているので熱拡散はないものとしています。
しかし、微小じょう乱が入り一様で無くなる場合は本来考慮しなくてはいけません。
粘性\(\nu\frac{\partial^2 u}{\partial x^2}\)も熱拡散も\(\alpha\frac{\partial^2 T}{\partial x^2}\)もいくら係数が小さくても微小じょう乱によって変動する場合は二階微分が大きくなるのでさすがに無視できなくなります(実現象と異なってきます)。
いきなり複雑に扱ってもよくわからなくなるかという思いで、ここはいったん粘性も熱拡散も無視しましょう。
そうしたときの、流体の基礎方程式を列挙します。
質量保存則
\begin{align*}\frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x}\big(\rho u\big)=0\cdot\cdot\cdot (1)\end{align*}
ナビエストークス方程式
\begin{align*}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=-\frac{1}{\rho}\frac{\partial P}{\partial x}+\nu\frac{\partial^2 u}{\partial x^2}\cdot\cdot\cdot (2)\end{align*}↓簡単に考えるため、粘性を無視します\(\nu=0\)
\begin{align*}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=-\frac{1}{\rho}\frac{\partial P}{\partial x}\cdot\cdot\cdot (2)\end{align*}
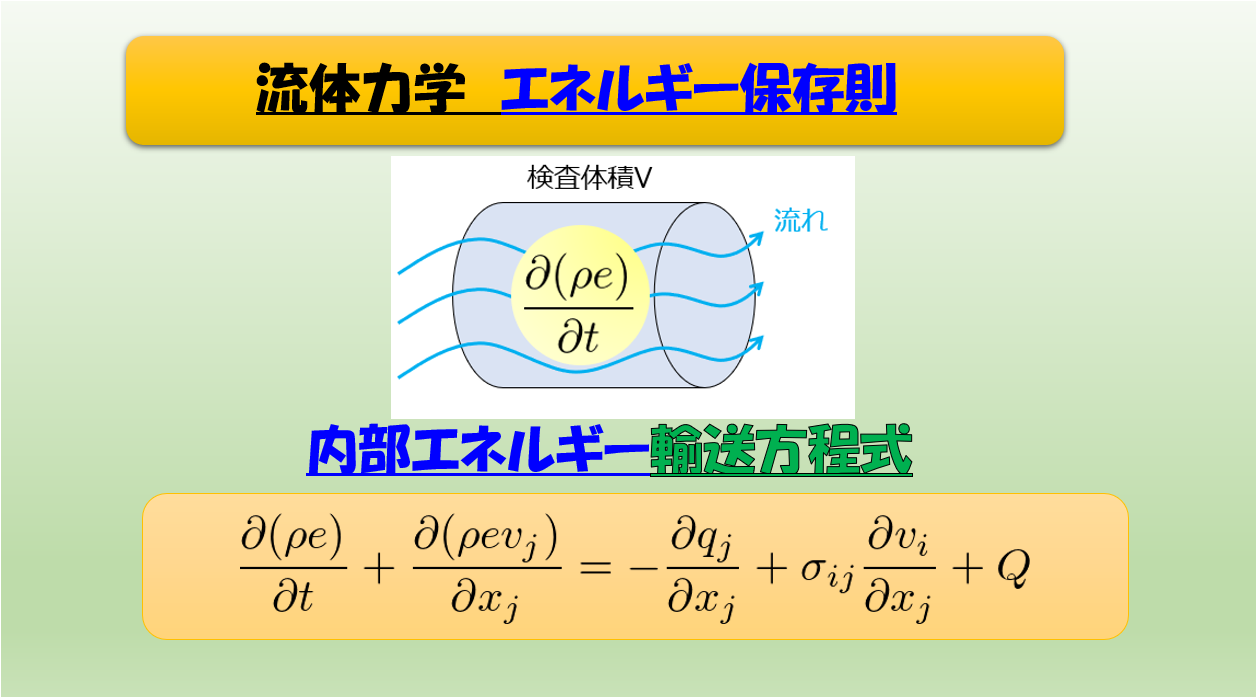
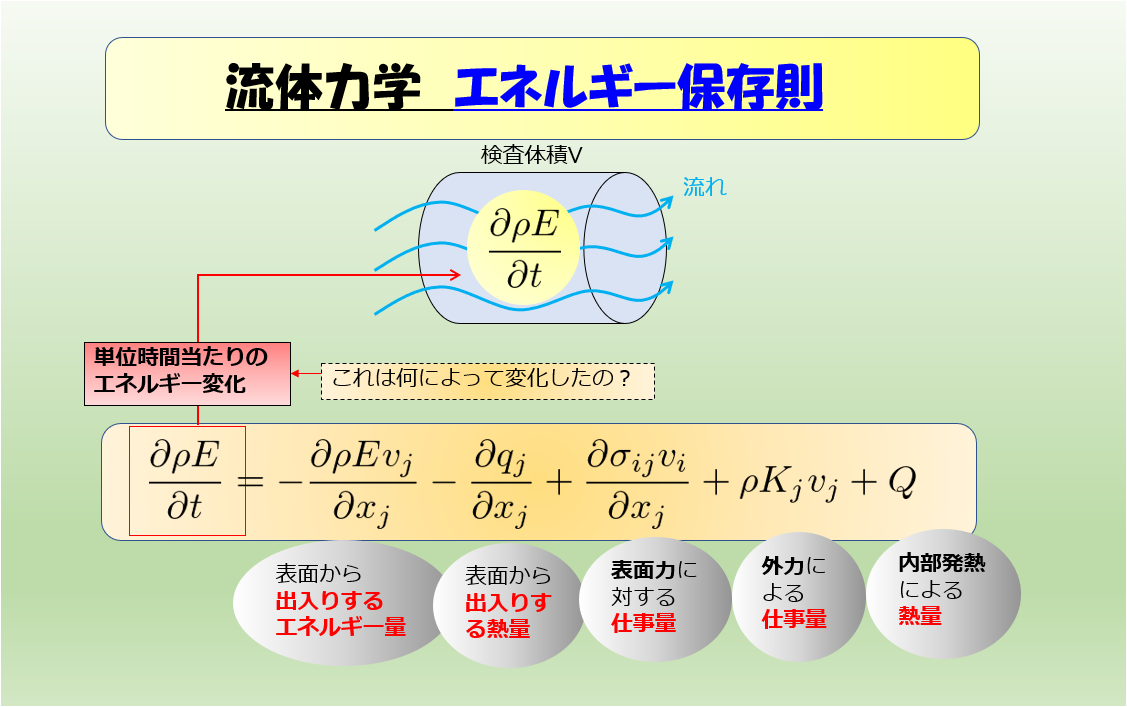
エネルギー保存則
\begin{align*}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}=\alpha\frac{\partial^2 T}{\partial x^2}\cdot\cdot\cdot (3)\end{align*}↓簡単に考えるため、拡散項を無視します\(\alpha\)
\begin{align*}\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}=0\cdot\cdot\cdot (3)\end{align*}
状態方程式
系の状態と言うのは、圧力\(P\)、密度\(\rho\)、温度\(T\)で決まるのですが、熱平衡状態にある場合は、
\begin{align*}f(P,\rho,T)=0\cdot\cdot\cdot (4)\end{align*}のような関係式(これを状態方程式と言う)があり、独立な変数は2つだけです。(未知数3つと(4)式なので自由度は2つ)
さらに、(4)式から温度の輸送は無視できるので温度は(4)式から除くことができ、
\begin{align*}f(P,\rho)=0\cdot\cdot\cdot (5)\end{align*}と書けます。
つまり、\(P\)が\(\rho\)に依存しているという形ですね。
ですので、(5)式を
\begin{align*}P=P(\rho)\cdot\cdot\cdot (6)\end{align*}と置けます。
微小じょう乱を導入
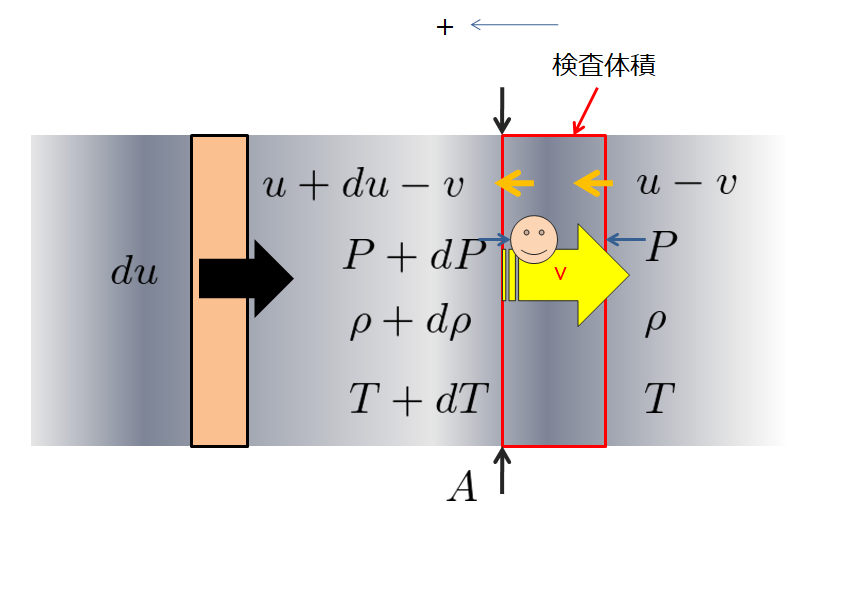
下記のように一様に流れている流体(速度\(u_{0}\)、密度\(\rho_{0}\)、圧力\(P_{0}\))に、微小じょう乱\({u}’、{\rho}’、{P}’\)を考えます。

そうすると、速度、密度、圧力はそれぞれ
- 速度:\(u=u_{0}+{u}’\)・・・(7)
- 密度:\(\rho=\rho_{0}+{\rho}’\)・・・(8)
- 圧力:\(P=P_{0}+{P}’\)・・・(9)
となります。
ここで考えたいのは、微小じょう乱\(\rho\)がどのような速度で伝播するかです。
さて、(7)(8)(9)式を(1)(2)に代入してみましょう。
結果
\begin{align*}\frac{\partial {\rho}’}{\partial t}+\rho_{0}\frac{\partial {u}’}{\partial x}=0\cdot\cdot\cdot (10)\end{align*}
\begin{align*}\frac{\partial {u}’}{\partial t}+\frac{1}{\rho_{0}}\big(\frac{dP}{d\rho}\big)_{0}\frac{\partial {\rho}’}{\partial x}=0\cdot\cdot\cdot (11)\end{align*}
いきなり結果を示しましたが、気になる方は下記を参考にやってみてください。
(1)式に(7)(8)式を代入
これは簡単です(^^)
微小じょう乱の2次の項は無視すると、
(2)式に(7)(8)(9)式を代入
右辺の分母については、\(\rho_{0}>>{\rho}’\)なので\(\rho_{0}+{\rho}=\rho_{0}\)。
さらに微小じょう乱の2次の項は無視すると、
ここで、右辺の\(P+{P}’\)は(6)式より「密度変動したことによって圧力変動が起こった」と考えるはずなので、
\(P+{P}’=P(\rho_{0}+{\rho}’)\)として、これを\(\rho=\rho_{0}\)のまわりでテーラー展開しておきましょう。
そして、xで偏微分を行って、
よって、
さてもう一息です。
\(\frac{\partial}{\partial t}\)×(10)ー\(\rho_{0}\)\(\frac{\partial}{\partial x}\)×(11)として、\({u}’\)を消しましょう。
そうすると、
となりました!(^^)!
ここで、\(a_{0}=\sqrt{\big(\frac{\partial P}{\partial \rho}\big)_{0}}\)と置いたらどうでしょう。
\begin{align*}\frac{\partial^2 {\rho}’}{\partial t^2}-a_{0}^2\frac{\partial^2 {\rho}’}{\partial x^2}=0\cdot\cdot\cdot (12)\end{align*}これは波動方程式ですね!(^^)!
つまり、微小な密度変動は\(a_{0}=\sqrt{\big(\frac{\partial P}{\partial \rho}\big)_{0}}\)で伝播することになります。
この密度伝播を音波と言います。
\begin{align*}a_{0}=\sqrt{\big(\frac{\partial P}{\partial \rho}\big)_{0}}\end{align*}を音速と言います。
ですので、密度変動は音速で伝播するわけですので、密度変動を考慮するかどうかというのはこの音速の値が相対的に無視できるかどうかということにつながりますね。
音速が流速に比べてものすごく大きい場合は、密度変動が一瞬で端まで伝播するかですから、それは密度変化がないというのと等価であると考えてよいですし、逆に音速が流速と同等である場合は、密度変動は決して無視できないということになります。
理想気体の状態方程式から空気や水の音速
結果だけ示しておきましょう(^^)/
| 物質 | 音速 |
| 空気0℃ | 331m/s |
| 水0℃ | 1407m/s |
水の音速が大きいですね(笑)
物理量の伝播は疎密波で伝わります。つまり、縦波で伝播していくので伝播するために媒介してくれるものがある方がより速く伝播することになりますよね。
ということを考えると、水は空気に比べて密度が大きいので音速が速いという理解になります。
ですので、多くの場合「水は非圧縮性流体(密度変動が無視できる流体)」として扱っても良いことになります。
でも音速と同等なくらいの流速であれば、水であっても圧縮性を考慮しなくてはいけないです(「水=非圧縮性流体」が必ず成り立つわけではないことに注意です)。
さらに、音速も温度依存しますので、いつも上記の速度で伝播するということではないということに注意しておきましょう(^^)/
まとめ
微小な密度変動は、
\begin{align*}a_{0}=\sqrt{\big(\frac{\partial P}{\partial \rho}\big)_{0}}\end{align*}で伝播する。音速
\begin{align*}a_{0}=\sqrt{\big(\frac{\partial P}{\partial \rho}\big)_{0}}\end{align*}


















参考になりましたー 😀
「さてもう一息です。∂/∂t×(10)ー∂/∂t×ρ0(11)」
の所の第二項は∂/∂t→∂/∂xが正しいと思います。
どうもお読みいただきありがとうございます。
おっしゃる通りです(‘ω’)
修正致しました。
早々に見ていただいてありがとうございます_(._.)_
「(4)式から温度の輸送は無視できるので…」の所が何となく等温過程っぽく見えてしまってやや誤解を生む気もするのですが、等エントロピー過程でもp=p(ρ)になることは変わらないのであまり問題でも無いでしょうか。(∂p/∂ρ)sという表現が一般的な気がするので少し気になっていました。
長文失礼しました!
ではでは。
コメント頂きありがとうございます。
見返してみるとそうですね。
僕の理解したことを追記しておきます。
(3)式を温度場の輸送でDT/Dt=0と見れば流れに沿って温度場が変化しないとなってしまいますね。
拡散項を無視することの本質は、圧力の微小変化を考える場合に、拡散項などが小さく(エントロピー変化が温度勾配の2乗に比例)なので、「微小圧力変動の場合は等エントロピー過程から拡散項を無視しても良いでしょう」と書くのが良さそうですね。
その辺の詳しい補足の記事を作成しておく方が良いと感じました。
また、(∂p/∂ρ)sと書くように議論を展開した方が良かったかもしれませんね。
(∂p/∂ρ)0と書いたのは、初期状態が一様流からなので、初期はエントロピーが一様で、「エントロピーが初期から変わっていないですよ」という意味で、(∂p/∂ρ)0と書いていました。
その意図もあまり書かれていなくてこれはちょっと不親切ですね(笑)
大変貴重な意見でありがとうございます。
少し考えたいと思います。
また貴重なご意見お待ちしております。
今後ともよろしくお願いします。