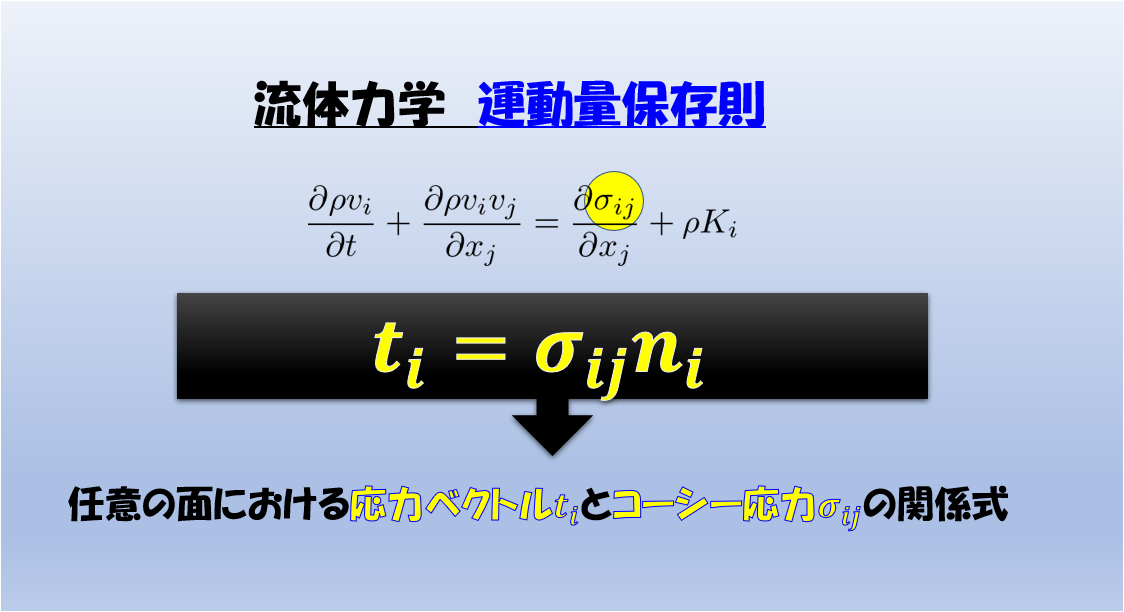
前回の記事では、コーシー応力\(\sigma_{ij}\)の物理的な意味と、その式を示しました。
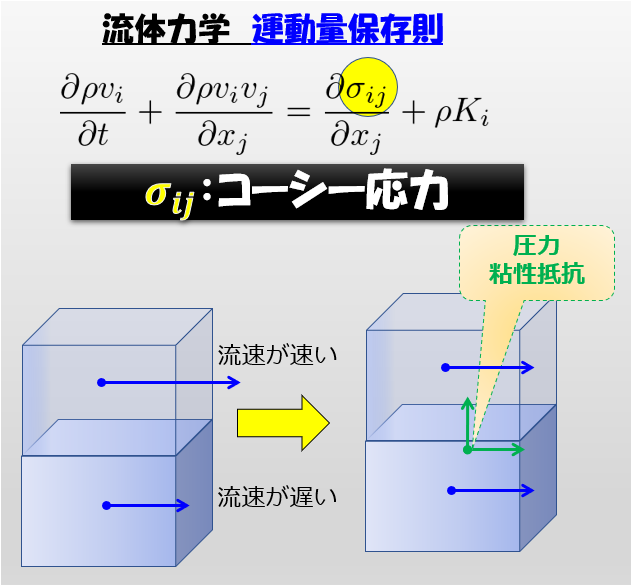
このコーシー応力\(\sigma_{ij}\)は、流体力学の運動量保存則の圧力項と粘性項に関わる内力で重要です。
運動量保存則
本記事を読むと以下のことがわかるようになります。
- 任意の面にはたらく応力ベクトルとコーシー応力の関係式がわかる
※下記の(1)式
キーワードは、「任意の面」と「応力ベクトルとコーシー応力の関係式」
任意の面にはたらく応力ベクトル\(\boldsymbol{t}\)
t_{1} \\
t_{2} \\
t_{3}
\end{pmatrix}\end{align*}
↓
\sigma_{11} & \sigma_{12} & \sigma_{13}\\
\sigma_{21} & \sigma_{22} & \sigma_{23}\\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{pmatrix}\begin{pmatrix}
n_{1} \\
n_{2} \\
n_{3}
\end{pmatrix}\cdot\cdot\cdot (1)\end{align*}
(1)式はこのように書いたりもします。
※添え字が2回続くと和を意味しています（アインシュタインの縮約記法）。
どうやって(1)式を導くのかですが、簡単です。
「任意の面\(S\)にはたらく力」と「三角錐の各面（面\(S\)以外）にはたらく力」とのつり合いの式を立てれば良いのです。
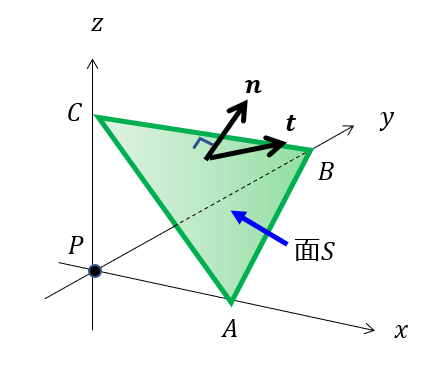
任意の面\(S\)を用意する（準備段階）
点\(P\)を頂点とする微小な三角錐\(PABC\)を考えます。
緑の面\(S\)にはたらく応力ベクトル\(\boldsymbol{t}\)とコーシー応力\(\boldsymbol{\sigma}\)との関係を知ることが本記事の目標となります。
※緑の面の面積は\(S\)
法線ベクトルと応力ベクトル
では、任意の面上の法線ベクトル\(\boldsymbol{n}\)と応力ベクトル\(\boldsymbol{t}\)を下記のように置きます。
ここは、文字を定義しただけですね。
また法線ベクトルは別の書き方では、
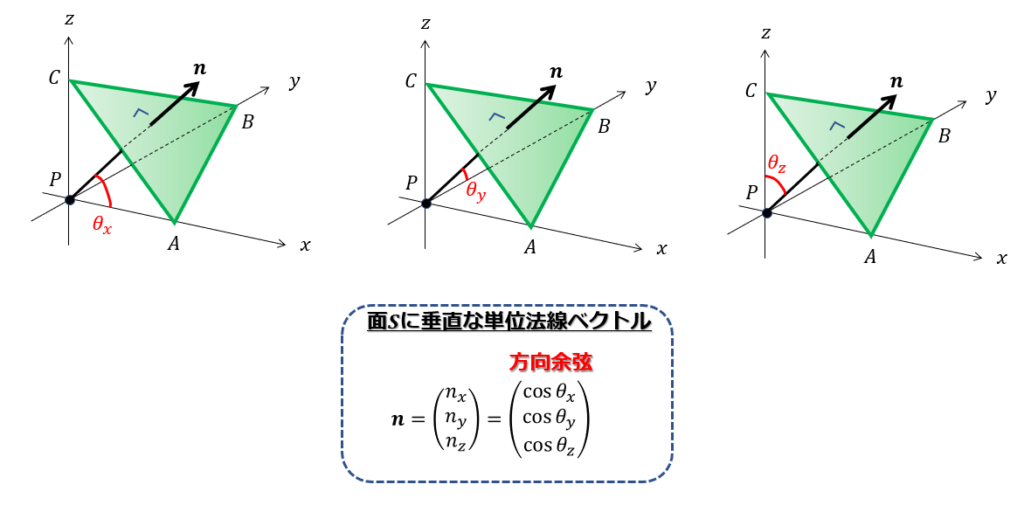
こんな感じで、「各軸におろした角度」を使って方向余弦を定義できます。
\cos\theta_{x} \\
\cos\theta_{y} \\
\cos\theta_{z}
\end{pmatrix}\cdot\cdot\cdot (3)\end{align*}
三角錐の各面の面積
続いては、三角錐の各面の面積を定義していきます。
- \(x\)軸に垂直な面の面積：\(S_{x}\)
- \(y\)軸に垂直な面の面積：\(S_{y}\)
- \(z\)軸に垂直な面の面積：\(S_{z}\)
このように「～軸に垂直な面の面積」を添え字を使って区別します。
絵で書くとこんな感じ↓
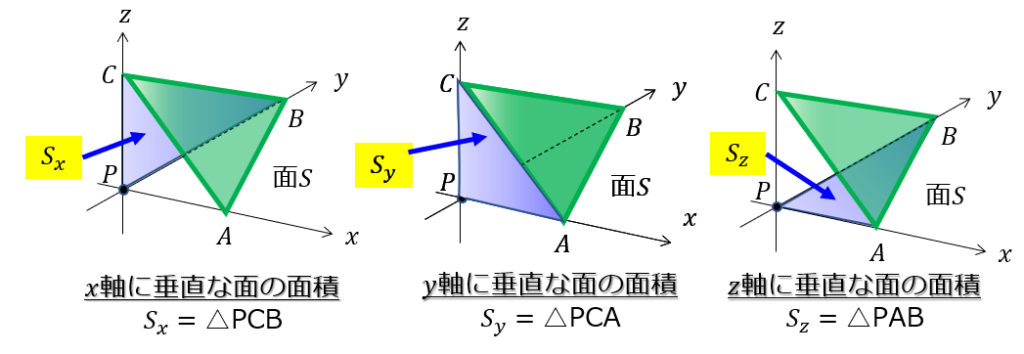
応力は「単位面積あたりの力」を意味していますので、各面にはたらく力を考えるときには、各面の面積を定義しておく必要があるので定義しました。
各面にはたらく応力ベクトル
続いて各面にはたらく応力ベクトルを書いていきます。
応力ベクトルは2種類あります。
- 面に対して垂直な方向の応力：垂直応力
- 面に対して平行な方向の応力：せん断応力
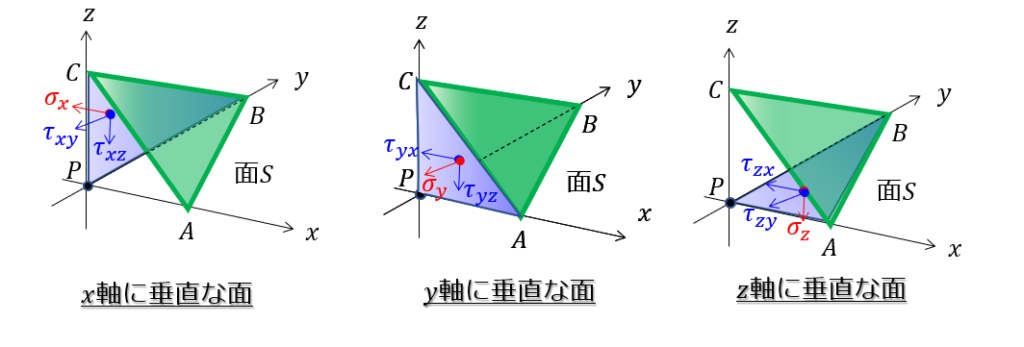
添え字が多くて少々煩雑に見えますが、添え字の意味を理解しておくとたいしたことはないです。
垂直応力は添え字がひとつしかないのでわかりやすいですが、せん断応力は添え字が２つあるのでどういった意味なのかを示しておきます。
これで準備段階は終わりました。
ようやく、任意の面にはたらく応力ベクトルと、三角錐の各面にはたらく力とのつり合いの式を考えることになります。
\(x\)軸方向の力のつり合い
どの軸も特別な軸というわけではないので、どれかひとつだけの軸について、どのような式が導けるのかを考えれば十分ですよね。
それを\(x\)軸にとることにります。
では、\(x\)軸方向の力のつり合いを考えていきます。
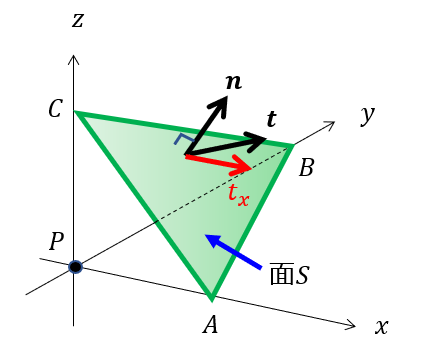
任意の面（緑色）にはたらく応力ベクトルの\(x\)方向の応力を\(t_{x}\)と置きます。
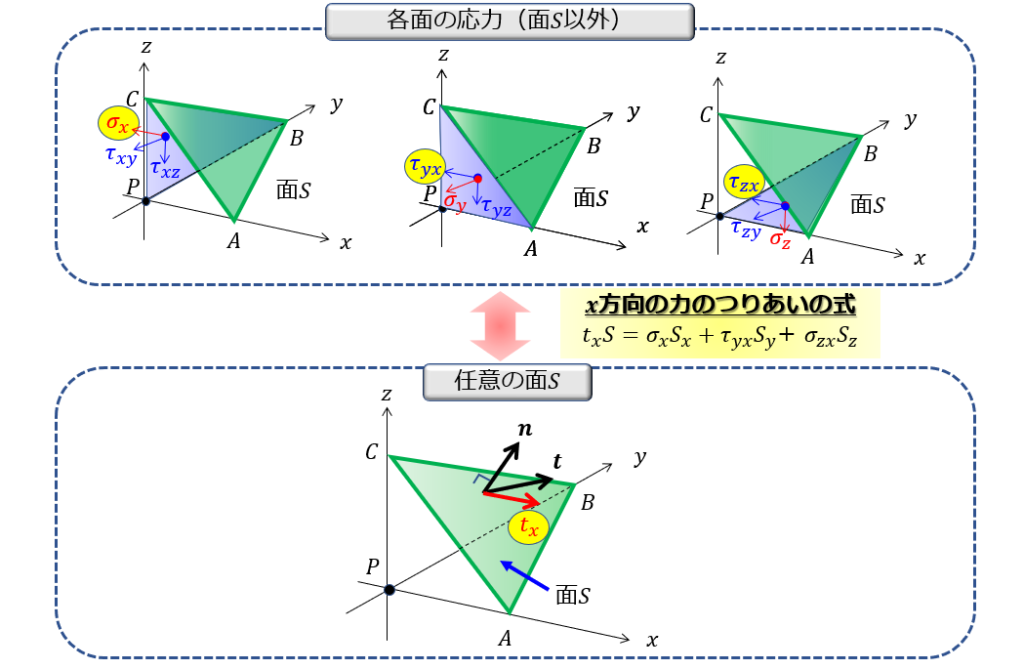
\(x\)方向の力のつり合いの式
と、こうのようになります。
まだ、これでは\(S\)や\(S_{x}\)などの面積の表記が邪魔ですよね。
そこで、\(S\)や\(S_{x}\)などの関係式を示しておく必要があります。
\(S_{x}\)は\(S\)を\(x\)軸方向に投影した面積
表題の通り、\(S_{x}\)は\(S\)を\(x\)軸方向に投影した面積です。
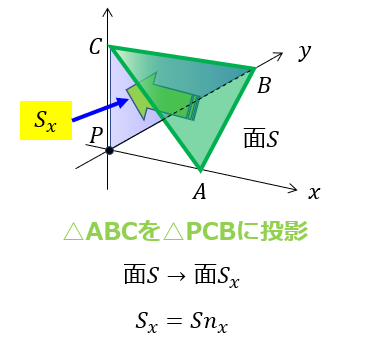
だから、
の関係式が成り立ちます。
よくわからないっていう人は、面で考えるからわかりにくいのだと思います。
法線ベクトル\(\boldsymbol{n}\)は面\(S\)に対して垂直なベクトルなのだから、面が線に見える方向から眺めてみれば良いです。
\(zx\)面方向から面\(S\)を眺めてみましょう。
そうすると、
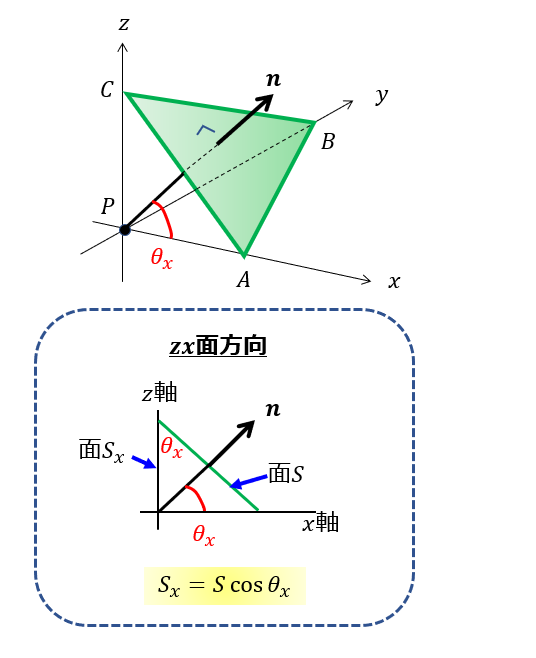
こんな感になります。
そこで(3)式の方向余弦を思い出しますと、
こうなることがわかりますよね。
だから、各面に対しても
が成り立ちますので、(5)(6)(7)式を(4)式に代入すると、両辺で\(S\)が消去されるので、
となります。
導けました(^^)/
\(y\)軸、\(z\)軸方向の力のつり合いも同様に考える
\(x\)軸方向が特別な軸ではないのですから、同じ考え方をすると\(y\)軸、\(z\)軸方向についても、
\(y\)方向の力のつり合いの式
\(z\)方向の力のつり合いの式
このようになります。
行列表示にする
さて、これを行列での表記にするととてもすっきりします。
\(x\)方向の力のつり合いの式
\(y\)方向の力のつり合いの式
\(z\)方向の力のつり合いの式
下記が(8)(9)(10)の行列での表記です。
\sigma_{x} & \tau_{yx} & \tau_{zx}\\
\tau_{xy} & \sigma_{y} & \tau_{zy}\\
\tau_{xz} & \tau_{yz} & \sigma_{z}
\end{pmatrix}\begin{pmatrix}
n_{x} \\
n_{y} \\
n_{z}
\end{pmatrix}\cdot\cdot\cdot (11)\end{align*}
ここで、\(x\)、\(y\)、\(z\)などの文字が添え字だと扱いにくい場合も多いので、添え字を数字に変えておきます。
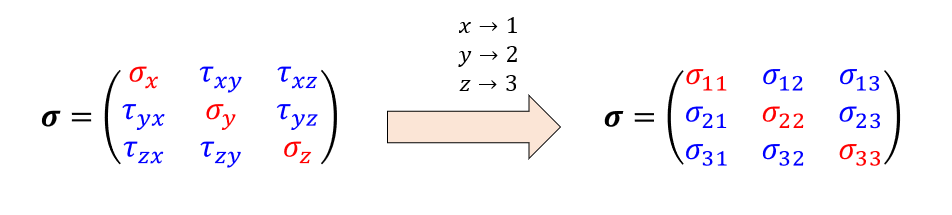
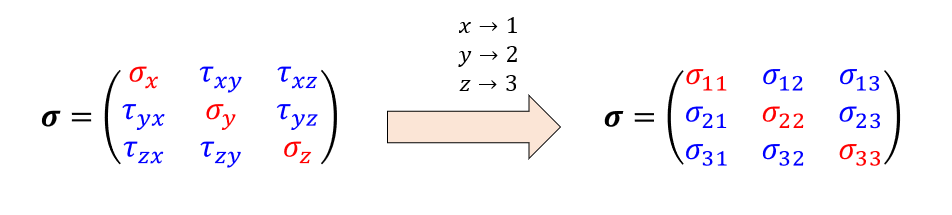
こんな感じで・・・
そうすると、冒頭で示した応力ベクトルとコーシー応力の関係式が導けたことになります。
\sigma_{11} & \sigma_{12} & \sigma_{13}\\
\sigma_{21} & \sigma_{22} & \sigma_{23}\\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{pmatrix}\begin{pmatrix}
n_{1} \\
n_{2} \\
n_{3}
\end{pmatrix}\cdot\cdot\cdot (1)\end{align*}
これでも十分よくまとまっていますが、もっとすっきりさせるためにテンソル表記にすることもあります。
まとめ
順を追って行けばそれほど難しくもなかったかもしれません。
任意の面にはたらく応力ベクトル\(\boldsymbol{t}\)
t_{1} \\
t_{2} \\
t_{3}
\end{pmatrix}\end{align*}
↓
\sigma_{11} & \sigma_{12} & \sigma_{13}\\
\sigma_{21} & \sigma_{22} & \sigma_{23}\\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{pmatrix}\begin{pmatrix}
n_{1} \\
n_{2} \\
n_{3}
\end{pmatrix}\cdot\cdot\cdot (1)\end{align*}
(1)式はこのように書いたりもします。
※添え字が2回続くと和を意味しています（アインシュタインの縮約記法）。
(2)式は何に使うのか？
よくありがちなのが、複雑で長い式を一生懸命計算していって導いた結果について、「ん？これはいったい何に使うのか？」ってなることです。
だからもう一度、「任意の面にはたらく応力ベクトル\(\boldsymbol{t}\)」をなぜ示したのかをおさらいすると、流体力学の運動量保存則の圧力項と粘性項に関わる内力を表現するためです。
※下記の\(\sigma_{ij}\)が何かを理解するためです。
運動量保存則
次回
少しづつイメージがつかめてきたところで次回は、流体力学の基礎式の一般系から運動量保存則を導きたいと思います。
↓流体力学の基礎式の一般系は下記の記事
Follow @t_kun_kamakiri
非常に図がわかりやすいです。どのように作成していますか？
ありがとうございます(^^)
パワポの2016バージョンを使っているので特に特別な方法は使っていません(笑)
↓これを最近模索中です。
https://www.mynote-jp.com/entry/TikZ-examples
こんにちは。連続体力学の初学者で、いつも勉強に利用させていただいております。
任意の面での応力についての解説文のなかで疑問が湧いたのですが、三角錐の各面にかかる力のつり合いを考えていますが、ここで力のつりあいが成立する物理的な要請ってあるのでしょうか？本質は力のつり合いではなく、応力がテンソル（線型写像）であることではないかと思いました。詰まる所、なぜ応力がテンソル表現なのか、という部分がうまく理解できません。単純に線型な物理モデルを扱っているだけのことなのか、それとも応力がテンソルというのは連続体力学で一般的な話なのでしょうか？。的はずれなコメントをしていたら申し訳ありません。
お読みいただきましてありがとうございます。
少々回答が長くなり申し訳ございません。
「Aさんが物体Bをある力で押すと、同じ力でAさんは物体Bから押し返されます」。これをAさんと物体Bを一体モノだと思うと今回考えている状況と同じです。
つまり内力なのでつりあっていること自体を要請しています。
それでも納得がいかない場合もあるかと思います。
その場合は、「最小作用の原理から仮想仕事の原理」というものを要請すると、自然と力のつりあいが導かれます。
つまりここで考えている力は内力なので力がつりあっていると状態が最も実現可能な状態と考えるのです。
力の作用面の法線の向きと力の作用方向とが一致してしていない応力成分（せん断応力）があるため、2階テンソルになっていると理解しております。
2階テンソルといっても、「共変テンソル、反変テンソル、混合テンソル」などありますが、申し訳ないですがそのあたりは勉強不足なのでこれ以上は回答ができません。
材料力学でも流体力学でも同じように連続体力学として応力を定義していますので、連続体力学では一般的ではないかと思っております。
返信ありがとうございます。私は社会人になってから物理の学習意欲が再燃したもので、久々に他人と物理の話ができて嬉しく思います。
ところで応力がテンソル表現になる理由について、返信を読んでもすぐには腑に落ちなかったのですが、あわせて以下のリンクを読んで一応納得できました。
https://www.gfd-dennou.org/arch/riron/renzoku/ouryoku/pub/ouryoku.pdf
応力について作用反作用を表現するとσ(-n)= – σ(n)が成立することはすぐに納得できたのですが、ここからσが線型写像であることを結論するのは飛躍があるので、悶々としていました。が、リンク先の説明にあるように応力が面積力であることを加味するとたしかに応力σがテンソルでなければならないことが説明できるな、と一応わかった気にはなりました。またわからないことがあったらコメントさせてください。