どうも(^^)/
本日の記事では、流体力学の基礎方程式の導出を行いたいと思います(^^)
こちらでちらっと基礎方程式について触れたのですが、今回は導出について触れたいと思います。
なぜ流体力学の基礎方程式の導出について書こうと思ったかと言いますと、流体力学の基礎方程式って力学などの運動方程式などと比べると、見た目がちょっと複雑に見えるのですよね。
本記事の目標
普通の教科書は以下の(1)~(3)の流体力学の基礎方程式をひとつひとつ導出するのですが、本記事ではもう少し統一した導出方法をお見せしましょう(^^)/
まず基礎方程式を並べてみましょう。
質量保存則
\begin{align*}\frac {\partial \rho }{\partial t}+\frac{\partial \rho v_{j}}{\partial x_{j}}=0\cdot\cdot\cdot (1)\end{align*}
運動量保存則
\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}
エネルギーの保存則
\begin{align*}\frac{\partial \rho E}{\partial t}+\frac{\partial \rho E v_{j}}{\partial x_{j}}=-\frac{\partial q_{j}}{\partial x_{j}}+\frac{\partial \sigma_{ij}v_{i}}{\partial x_{j}}+\rho K_{j}v_{j}+Q\cdot\cdot\cdot (3)\end{align*}
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
熱力学の状態方程式
\begin{align*}f(P,T,\rho)=0\cdot\cdot\cdot (4)\end{align*}
こんなのひとつひとつ別個でどうやって導出するかなんて覚えれるかっていう感じです。
上述の(1)~(3)式の流体力学の基礎方程式については、実は一般的な考え方に従って同じやりかたで導出しているのですよね。
それが流体力学の基礎方程式の一般系です。
基礎方程式の一般系
流体力学は結局のところの何かの物理量\(\Phi\)の輸送(流れ)を記述しているに過ぎません。
\(\Phi\)が、「質量\(\rho\)」なのか「運動量\(\rho\boldsymbol{v}\)」なのか「エネルギー\(\rho E\)」なのかの違いであるだけです。
もう一度言いますが、
結局のところの何かの物理量\(\Phi\)の輸送(流れ)を記述しているに過ぎません。
なので何も難しいことを考えずに、
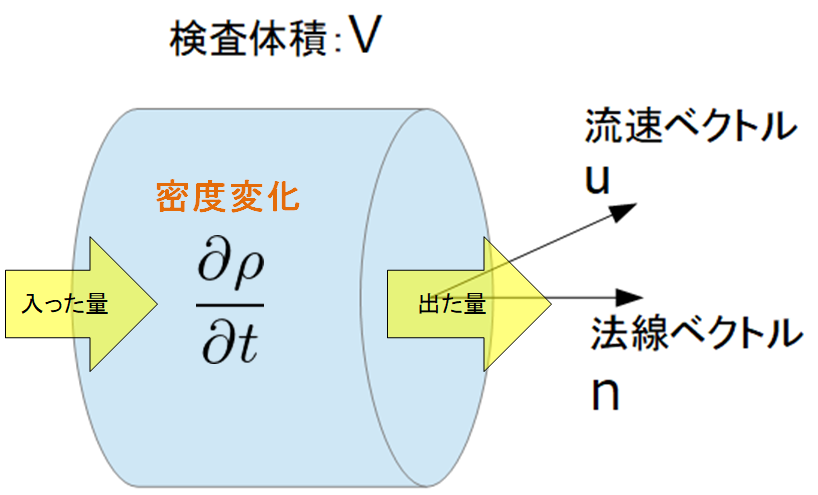
下記のような検査体積\(V\)という微小体積から、
(A)単位時間当たりの物理量\(\Phi\)の減少量
=
(B)流れによる表面からの出入り
+
(C)表面からの作用
+
(D)検査体積内での発生・消滅、体積力による仕事
と、このように考えれば良いということになります。

ひとつひとつ見ていきましょう(^^)/
(A)単位時間あたりの物理量\(\Phi\)の減少量
検査体積\(V\)で、単位時間あたりに減少する物理量ということなので、
ですね。
それで、これが何が原因で変化したのかを(B)(C)(D)で表現してやれば良いということになります。
検査体積は静止している状況を考えているので、時間微分と積分を入れ替えます。
(B)流れによる表面からの出入り
ある物理量が表面に垂直に単位時間あたりに出ていく量ですから、
と書けます。
ここで、ガウスの発散定理より、
ベクトル表記で下記のように書いている場合が多いかもしれませんが、本記事では統一して上述のようにテンソル表記にしておきます。
もう一度書くと、表面からの出入りは下記のように書けます。
流束(flux)\(\Phi v_{j}\)の発散ですね(^^)
ただし、↑の式では出入りした量(出た入った量が正の値)を示していますので、「(A)の増加量=(B)の増加量」にするためにマイナスを付けておきます。
(C)表面からの作用
表面からの作用ですが、これは今原因はよくわからない量になりますので、ひとまず何か「単位面積あたりに\(a\)という力が作用している」というくらいに捉えておいて下記のように書いてみましょう。
今は一般的な形式に従って書きたいので、(7)が何かは具体的に物理量\(\Phi\)を決めてから考えることにします。
(D)検査体積内での発生・消滅、体積力による仕事
検査体積内での発生・消滅ですが、これもまだよくわからない量なのでひとまず下記のように書いてしまいましょう。
今は一般的な形式に従って書きたいので、(8)が何かは具体的に物理量\(\Phi\)を決めてから考えることにします。
(5)=(6)+(7)+(8)をつなげると・・・
さて、すべての式をつなげてみましょう(^^)/
こんな感じになりましたね。
まとめ
流体力学の基礎方程式の一般系を導きました。
基礎方程式の一般系
\begin{align*}\int\frac{\partial \Phi }{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (9)\end{align*}
案外簡単でしたね。
ちなみに同じ添え字の場合はΣで足すという暗黙の了解(アインシュタインの縮約記法)として表記しています。
これをもとに物理量\(\Phi\)が、
質量\(\rho\)なら(9)式は、「質量保存則」になります。
「質量保存則」の記事はこちら
運動量\(\rho \boldsymbol{v}\)なら(9)式は、「運動量保存則」になります。
「運動量保存則」の記事はこちら
エネルギー\(\rho E\)なら(9)式は、「エネルギー保存則」になります。
「エネルギー保存則」の記事はこちら
単位時間あたりに変化した物理量(左辺)が、何によって変化したか(右辺)を記述すれば、流体力学の基礎方程式が導けるというわけですね。
お勧め参考書
流体力学を学ぶにあたってお勧めの参考書をいくつか紹介しておきます。
こちらは僕が流体力学を学ぶ際にはじめて購入した流体力学の書籍です。
まさかの「前編」しかありません。後編を書ききる前に著者が亡くなられた非常に残念でなりません。
それでも、流体力学を基礎からきっちり書かれていて、ものすごく理解しやすいです。
次は、巽さんの書籍を紹介します。
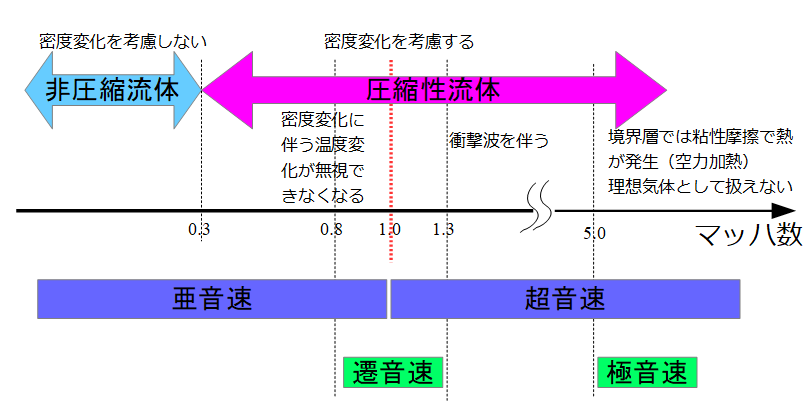
流体力学は非圧縮性と圧縮性の流れで少し説明が違ってくるのですが、こちらの参考書は両方の内容がよくまとまって書かれています。
実際、圧縮性の内容を深く学びたい方は以下の参考書を手に取るのが良いでしょう。
この書籍は圧縮性の流れのみ注力した参考書で、結構難しい内容です。
↑ちなみに第2版が出るようです。
もっと、初心者レベルから流体力学を学びたいという方には以下の参考書が気楽に学べるかと思います。