流体力学質量保存則（連続の式）の導出

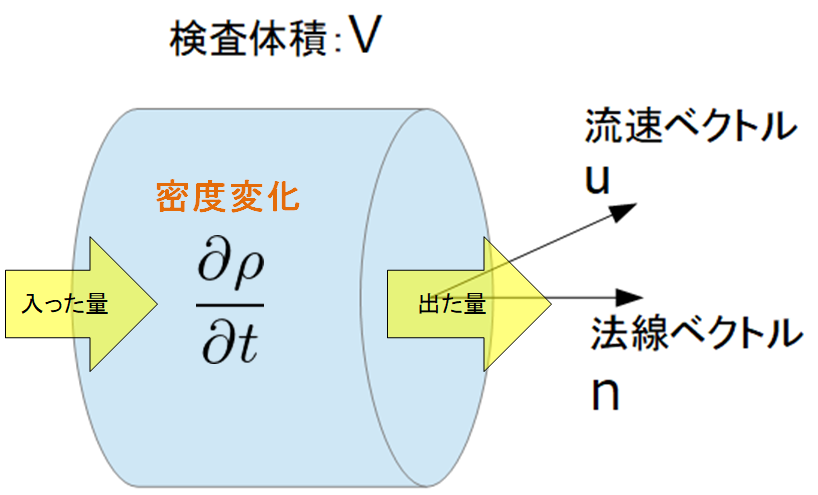
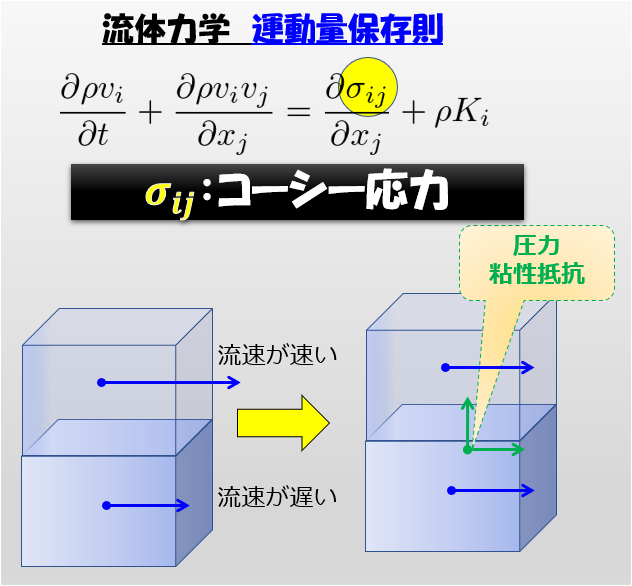
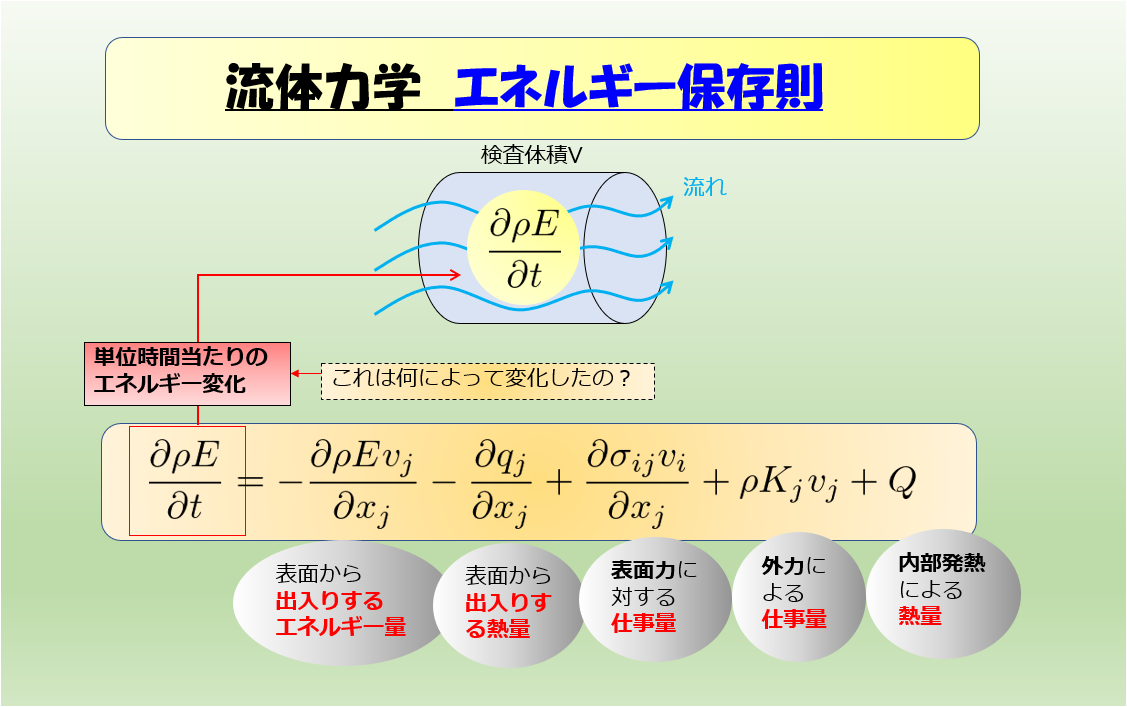
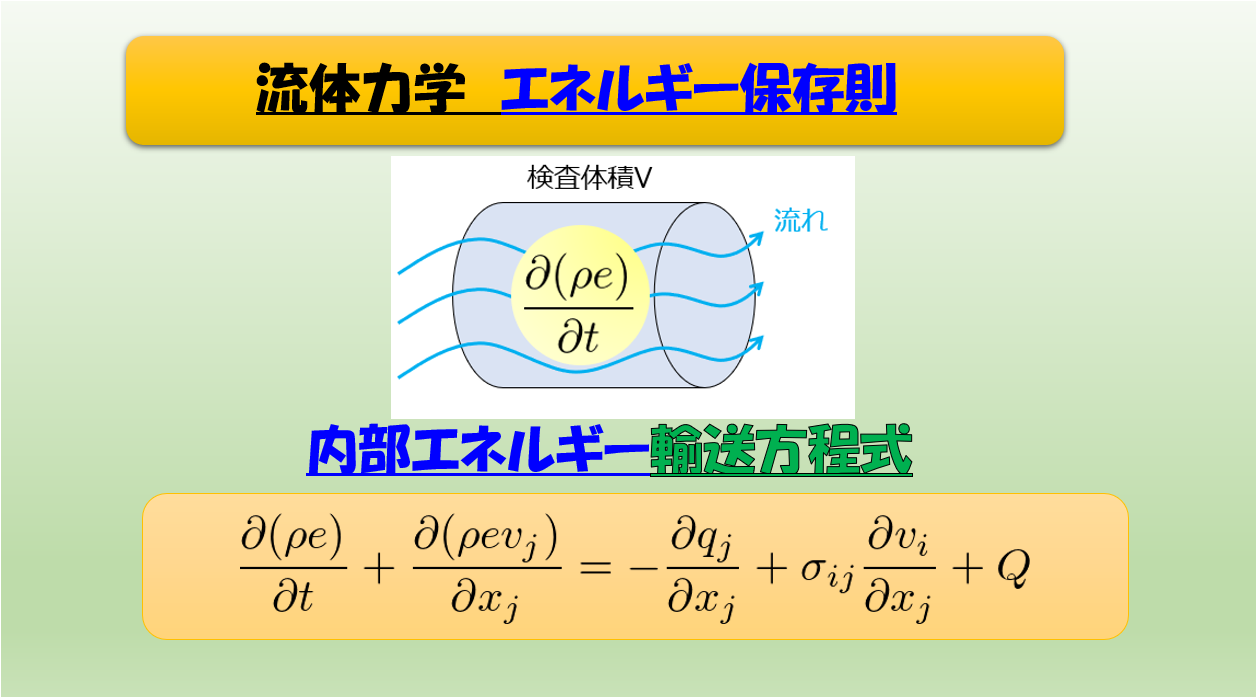
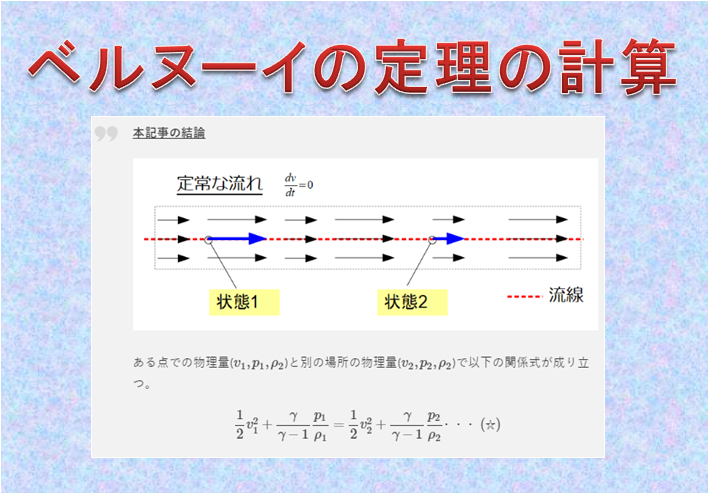
前回は、流体力学の基礎方程式の一般系を導きました。

基礎方程式の一般系

\begin{align*}
\int \frac{\partial \Phi}{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (\diamondsuit)\end{align*}

考え方はとてもシンプルで・・・

(A)単位時間当たりの物理量\(\Phi\)の減少量

=

(B)流れによる表面からの出入り

＋

(C)表面からの作用

＋

(D)検査体積内での発生・消滅、体積力による仕事

と、このように考えれば良いということになります。

と、このように考えて式を立てました!(^^)!

本日は、(\(\diamondsuit\)）の式を使って

質量保存則を導きたいと思います(^^)/

質量保存則（連続の式）

\begin{align*}
\frac{\partial \rho}{\partial t}+\frac{\partial (\rho v_{j})}{\partial x_{j}}=0\end{align*}

↓∇演算子で慣れている人もいるかもしれませね。

\begin{align*}
\frac{\partial \rho}{\partial t}+\boldsymbol{\nabla}\cdot(\rho\boldsymbol{v})=0\end{align*}

ちなみに、\(\frac{\partial (\rho v_{j})}{\partial x_{j}}=\sum_{i}\frac{\partial (\rho v_{j})}{\partial x_{j}}\)です。

同じ添え字の場合はΣで足すという暗黙の了解（アインシュタインの縮約記法）として表記しています。

(\(\diamondsuit\)）の一般系から「質量保存保存則」の導出

\begin{align*}
\int \frac{\partial \Phi}{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (\diamondsuit)\end{align*}

上記のようないわゆるある物理量\(\Phi\)の輸送方程式を導出したので、そのある物理量を決めれば、その物理量の輸送方程式が導出できるというわけです。

で、今回のある物理量とは「密度：\(\Phi=\rho\)」のことです。

”質量保存”と言っているわけですので、検査体積内の「単位当たりの質量変化＝出入りした質量の総和」となります。

ゆえに、(C)と(D)を考慮しなくても良いです。

もし、質量保存を破るような「質量の注入」などがある場合は(D)の効果も式として考慮しなければなりません。

ここでは、\(a=0,b=0\)として

「密度：\(\Phi=\rho\)」とおいて（\(\diamondsuit\)）に代入しましょう。

\begin{align*}
\int \frac{\partial \rho}{\partial t}\ dV=-\int \frac{\partial (\rho v_{j})}{\partial x_{j}}dV\cdot\cdot\cdot (1)\end{align*}

そして、任意の検査体積で(1)式が成立するためには、

\begin{align*}
\frac{\partial\rho}{dt}=- \frac{\partial (\rho v_{j})}{\partial x_{j}}\end{align*}

⇔左辺にもってきて

\begin{align*}
\frac{\partial\rho}{dt}+ \frac{\partial (\rho v_{j})}{\partial x_{j}}=0
\cdot\cdot\cdot (2)\end{align*}

このように質量保存則が導けました(^^)/

まとめ

基礎方程式の一般系

\begin{align*}
\int \frac{\partial \Phi}{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (\diamondsuit)\end{align*}

に\(a=0,b=0\)として「密度：\(\Phi=\rho\)」とおいて（
\(\diamondsuit\)）に代入すると、

↓質量保存則が導けました。

\begin{align*}
\frac{\partial \rho}{\partial t}+ \frac{\partial (\rho v_{j})}{\partial x_{j}}=0
\cdot\cdot\cdot (2)\end{align*}