流速の微小じょう乱は音速で伝播する

どうも(^^)/

前回下記の記事で「流体の密度の微小じょう乱（密度の微小な変動）は音速で伝播する」というのを、密度と速度の微小じょう乱を考えて波動関数を導くことで示しました。

結論から、密度の微小じょう乱は音速で伝播するので、水のような密度の大きい物質は密度伝播がしやすく、音速が非常に大きい（常温で約1400m/s)という話をしました。

ゆえに、水のような液体は流体現象を考える際には非圧縮性の流体として扱っても差し支えがないことになります。

流れの圧縮性を考慮するかどうかは、音速がとても重要なパラメータになるので、また違った視点から音速の式を導きたいと思います。

微小じょう乱は音速\(a\)で伝播する

早速音速の式を導出するのですが、考え方は下記のように、

流速：\(u\)
圧力：\(P\)
密度：\(\rho\)
温度：\(T\)

で流体が一様に流れている状態に速度\(u+du\)の平板で左から押してやるというのを考えます。

そうすると、平板から離れたところでは平板が押されたことによる影響が小さいので、微小な速度の変動というのは無く、元々の物理量のままでありますが、平板から近い場所では平板が押されたことによる物理量の微小変動というのが影響します。

※影響しないというと語弊がありますが、あとでこの変動が音速で伝播するということを示すので、非圧縮性の流体として扱える物質は実質、この微小じょう乱は一瞬で左から右へ伝播することになります。

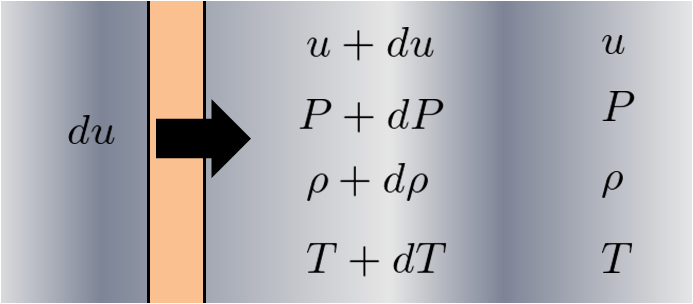
このように平板に近い場所では、

流速：\(u+du\)
圧力：\(P+dP\)
密度：\(\rho+d\rho\)
温度：\(T+dT\)

となります。

そしてこのように微小じょう乱は音速で伝わります。

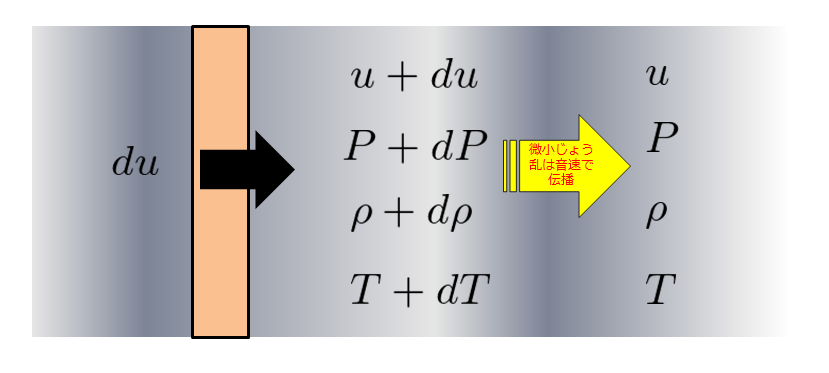
ただし、元々流速\(u\)で流れているので、平板が水を押したことによる影響は、一様流速\(u\)にプラスして音速で伝播します。

では、この音速を導いてみましょう(^^)/

音速を導いてみましょう

ただ流体を外から見たような座標系で考えるのは考えにくいのです。

なぜなら、流体の微小じょう乱が音速で伝播するので非定常な流れなので外から見ていると質量の保存が成り立たなくて扱いづらいです。

なので、その微小じょう乱の伝播速度である波面（音速）の上での定常流として座標系で考えることにします。

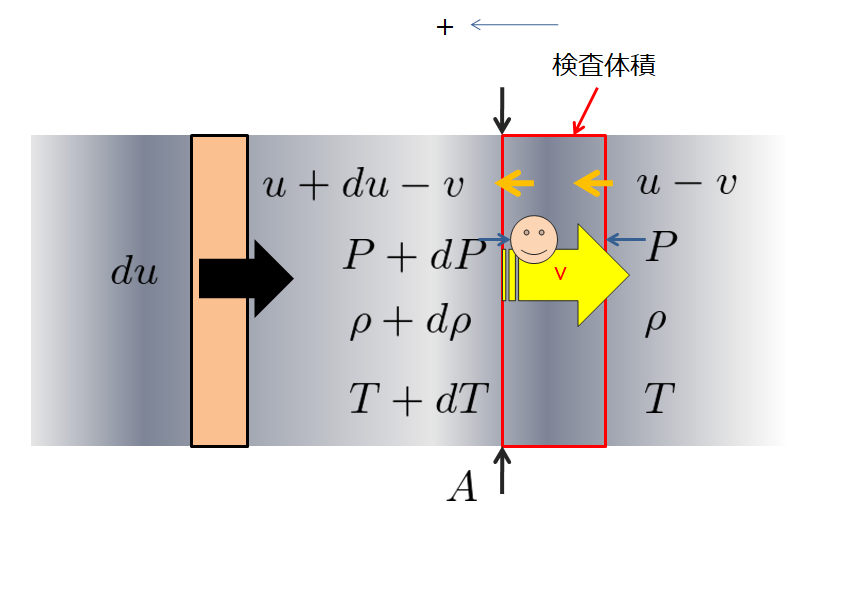
↑こんな感じです。

流体の通過幅の面積は\(A\)とします。

元々、一様に\(u\)で流れていたのでそれに微小じょう乱も加えた流速を\(v\)と置きます。

\(v\)の座標系に乗ったと考えたら、流速が音速より遅い場合（その場合の方が多いので）、赤枠で囲った検査体積内に右から左へ流入して流出していくと考えた方がやすそうなので、左をプラスの軸にします。

質量保存則

さて、質量保存則は上の検査体積の右から質量流と左へ出て行った質量流が同じであることから、

⇔

となります。

運動量保存則

運動量保存については、「単位時間当たりの運動量変化＝力」というように考えます

質点だと、

と書けるように、こういった考え方で流体についても考えます。

赤色の検査体積の質量は、流体が単位時間あたりに\((u-v)\)進むので

ですね。

なので、運動量保存は

\(F\)は検査体積内に両側からかかる力です。

今の場合は水圧、つまり圧力による力ですので、力と面積を掛け合わせて

となります。

よって、(2)式は、

となります。

(2)と(4)から\(du\)を消去します。

すると、

そして前回の記事で、音速は

であることを示しましたので、⑤式を見ると「元々の一様流\(u\)に変動分として音速\(a\)が加わっている」ことがわかります。

つまり、微小じょう乱は音速で伝播することが導けたのです(^^)/

まとめ

微小じょう乱は、

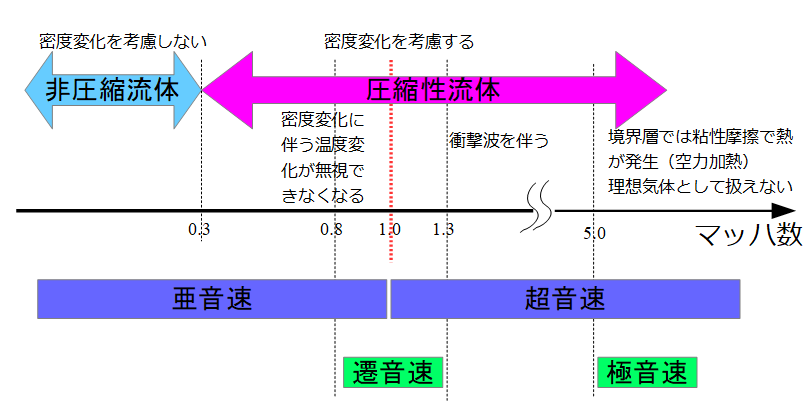
では、流速が音速よりも早く流れている場合はどうなっているのでしょうか？？

その場合はマッハ数が1以上の超音速流れと呼ばれます。

超音速流れについては、大変興味深いのでいずれ記事にまとめたいと思います(^^)/

ではこの辺で♪

参考文献