OpenFOAMで2次元円柱まわりの流体解析（力学的相似性の検証）

どうも(^^)/

本記事の目的

流体力学の力学的相似性の検証

前回の記事で、流れのパターンはレイノルズ数Reだけで決まるというのを説明しました。

↓こちらです。

前回の記事はこちら

流体力学の力学的相似性

それが本当なのかフリーの流体解析ソフトOpenFOAMを使って検証しようと思います。

力学的相似性：おさらい
力学的相似性：検証
力学的相似性：解析結果
まとめ
ちなみに・・・

力学的相似性：おさらい

軽くおさらいをしておくと、非圧縮性流体におけるナビエストークス方程式は、

\begin{align*}\frac{\partial \boldsymbol{v}}{\partial t}+\big(\boldsymbol{v}\cdot\boldsymbol{\nabla}\big)\boldsymbol{v}=-\frac{1}{\rho}\boldsymbol{\nabla}P+\nu\boldsymbol{\nabla}^2\boldsymbol{v}\cdot\cdot\cdot (1)\end{align*}

ですが、これを

代表的な長さL
代表的な速度V

として、無次元化を行うと、

\begin{align*}\frac{\partial {\boldsymbol{v}}’}{\partial {t}’}+\big({\boldsymbol{v}}’\cdot{\boldsymbol{\nabla}}’\big){\boldsymbol{v}}’=-{\boldsymbol{\nabla}}'{P}’+\frac{1}{Re}\boldsymbol{\nabla}’^2{\boldsymbol{v}}’\cdot\cdot\cdot (2)\end{align*}

と、このようになります。

ですので、(2)式を見る限りでは数値計算上ではレイノルズ数Reさえ同じであれば、システムがどのような大きさであっても流れのパターンは同じになるはずです。

↑これを流体力学の力学的相似性と言います。

力学的相似性：検証

環境

OpenFOAM: ver4.x
Dexcs2016 OpenFOAM
ソルバ：pisoFoam

参考資料：>>pisoFoamによる 2次元円柱周りの流れの解析

↑今回はこちらのわかりやすい資料を参考にさせて頂きました。ありがとうございます。

解析条件

解くべき方程式

ナビエストークス方程式
※非定常解析
※温度場の輸送方程式は解かない
※非圧縮性流体として扱う
※乱流モデル無し

物性値

動粘性係数：\(\nu=1.0\times 10^{-5}\)

次元

2次元

時間

タイムステップ：クーラン数指定

終了時刻：10秒

検証マトリクス

レイノルズ数がRe=20の場合と、Re＝200の場合の２つを例にとって検証します。

以下の①～④の４つのケースを検証します(^^)

		Re：レイノルズ数
		Re=20(双子渦）	Re=200(カルマン渦）
L：円柱サイズ	10mm	①（流入速度0.02m/s)	③（流入速度0.2m/s)
L：円柱サイズ	1mm	②（流入速度0.2m/s)	④（流入速度2.0m/s)

※動粘性係数は\(\nu=1.0\times 10^{-5}\)

「①と②」、「③と④」がそれぞれ流体力学的に相似ということになりますね。

ちなみに、ここでいう代表長さは円柱の直径、代表速度は左から流入する速度です。

上の絵を参考にすると、

①③は「円柱の背後に双子渦が発生」

②④は「円柱の背後に渦が放出されて渦配列を形成（カルマン渦）」

になりそうですね(^^)

実に面白い(笑)

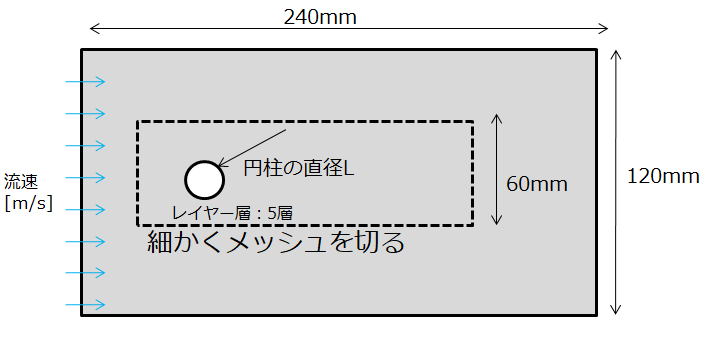
計算領域

検証マトリクスの①③については、下記のサイズで計算を実行。
※検証マトリクスの②④は、このモデルを0.1倍にスケール変換して計算（そのぶんレイノルズ数を合わせるために速度は10倍）。

力学的相似性：解析結果

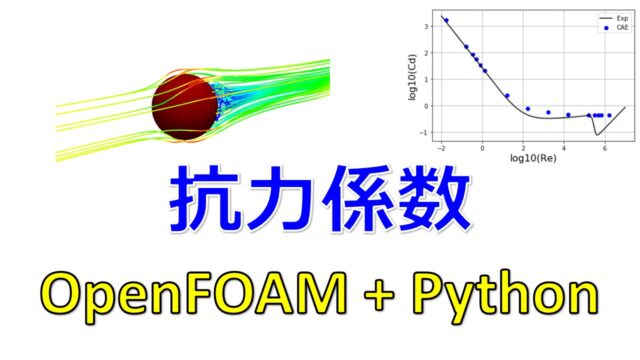
さてモデルを作成して、計算してみましたので速度のコンター図と流線を示します!(^^)!

		Re：レイノルズ数
		Re=20(双子渦）	Re=200(カルマン渦）
L：円柱サイズ	10mm	①（流入速度0.02m/s)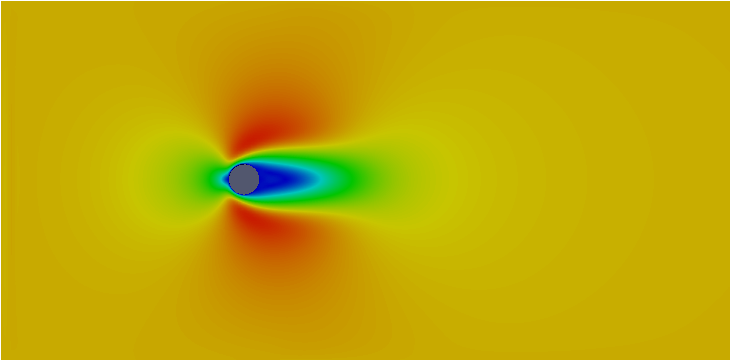	③（流入速度0.2m/s)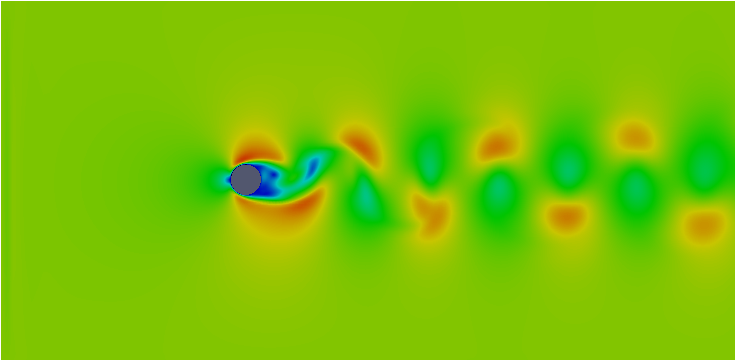
L：円柱サイズ	1mm	②（流入速度0.2m/s)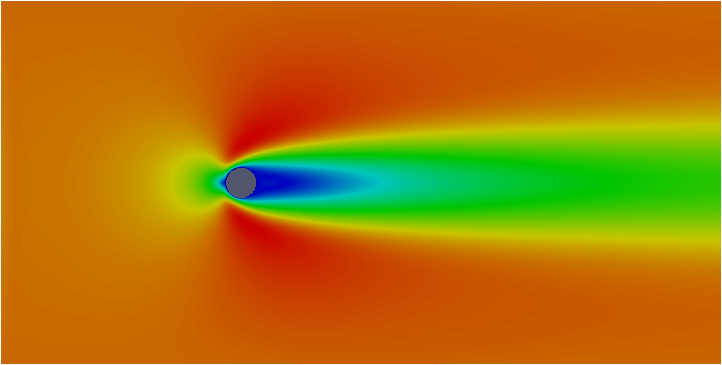	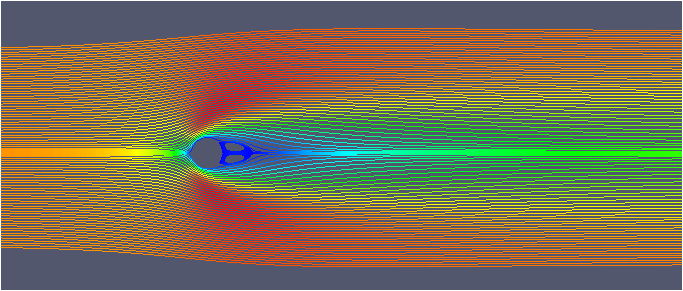④（流入速度2.0m/s)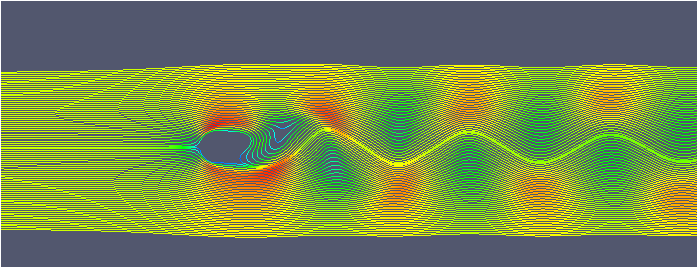

レイノルズ数を合わせると似たような流れのパターン(「①と②」「③と④」)になりましたね(^^)

①②の円柱背後の双子渦は見えますかね(笑)

まとめ

流体力学の力学的相似性のイメージを掴んで頂けたでしょうか？

本日の検証結果

流れのパターンはレイノルズ数Reだけで決まる。

今回の例は非常にわかりやすく、単純であったのでうまく力学的相似性が見れましたが、実現象では重力など他の外力も加わりますので、レイノルズ数Reが同じならば必ずしも同じ流れになるというわけではありません。

温度の影響など、実現象は色々とありますので・・・・

しかし、解析上は(2)を見て頂ければわかる通りレイノルズ数Reしかパラメータがありませんので、今回のような検証結果になるのは当たり前かもしれません。

流体力学にはレイノルズ数Reの他に色々な流れを特徴づける無次元量がありますので、それを全て揃えてはじめて全く同じ流れになるわけですが、あまり現実的ではありませんよね(*_*;

良い例でいうとフルード数などでしょうかね。
>>フルード数

ちなみに・・・

結構、計算が破綻しないように工夫したりするのは難しいのです(*_*;

最初に検証マトリクスとの③から円柱サイズを10倍にしたもの（速度は0.1倍）を④にしていたのですが、渦を形成するまでがものすごく時間がかかってしまいました。

確かに円柱サイズを10倍（速度は0.1倍）にすると、時間スケール\(t=L/V\)のものを、\(t=10L/0.1V=100L/V\)となり、もとの時間スケールの100倍になるので、これではいくらレイノルズ数を合わせているからといっても、時間スケールが大きすぎて渦形成するまで待っていられません(笑)

というわけで、時間スケールを小さくする方向になるように今回のような②④の条件を選んだというわけです!(^^)!

ただ速度が速くなる分、タイムステップも細かくしないと計算が破綻するので注意が必要ですが、今回はクーラン数でタイムステップを指定したので特に気にはしていませんでした。

また、常温で流速が約100m/s以上（マッハ数が約0.3以上）である流れの場合は、密度変化の伴う圧縮性流体であるため、その場合に非圧縮性流体として解析計算を行うと計算精度は著しく悪くなります（計算はできてしまいますが・・・）
計算精度が悪いというのは、実現象を再現するための数理モデルや離散化手法の選択を誤っているのでそれをどれだけ良いスキームで解いてもそりゃー実験と合うわけがありませんという意味です。

CAEはこういったように、往々にしてとりあえず計算はできちゃうのです(笑)

しかし、

(1)物理現象を再現しうる数理モデル

それから

(2)その数理モデルをコンピューター上で解くための離散化手法

この(1)(2)をよく考察しないと、「ま～計算はできちゃいましたが、合っているかわかりません(笑)」ってなるので、この辺りはよく考察して解析をしなくてはいけませんね。