【力学：強制振動】2階非斉次線形微分方程式の解法をわかりやすく解説する

2020年7月頃から一ヶ月ほど、物理の質問サービスをしています。

カマキリ

一ヶ月で30件くらい対応しました！受験勉強のようです_(._.)_

特に多かった質問として、以下の微分方程式の解法に関する質問です。

ひとつが、↓これ。

ダンパーの振動の運動方程式

\begin{align}m\frac{d^2x}{dt^2}=-D\frac{dx}{dt}-kx\tag{1}\end{align}

※本記事は、↓こちらの内容を読んでいることが前提となります。

前回の記事

【力学：減衰振動】2階斉次線形微分方程式の解法をわかりやすく解説する

もうひとつが、↓これ。

強制振動の運動方程式（←本記事の内容）

\begin{align*}
m\frac{d^2x}{dt^2}=-kx-D\frac{dx}{dt}+F_{0}\sin\Omega t \tag{2}
\end{align*}

この2つの微分方程式の解法についての質問が結構ありました。

僕が学生時代にもこの手の問題というのは、理解に苦しみました。
なぜなら、大学に入ってはじめて触れる微分方程式というものだからです。

前回の記事で(1)の解法は解説済みなので、本日は(2)の解法の解説をしたいと思います。

本記事の内容

微分方程式、

\begin{align*}
m\frac{d^2x}{dt^2}=-kx-D\frac{dx}{dt}+F_{0}\sin\Omega t \tag{2}
\end{align*}

の解法を理解する。

微分方程式を理解するだけではなく、

(2)の物理的な意味は何かを理解する
(2)の微分方程式の解法を理解する

こちらの2点を詳しく解説します。

では、さっそくやっていきましょう！

強制振動の運動方程式
2階非斉次線形微分方程式とは何か
2階非斉次線形微分方程式の解法
\(f_{0}=0\)の場合の一般解を求める
強制振動の特殊解\(x_{2}(t)\)を求める
2階非斉次線形微分方程式の一般解は？
まとめ
おまけ：空気抵抗は本当に速度に比例するのか
おすすめの参考書

強制振動の運動方程式

今回考えるのは以下のような問題です。

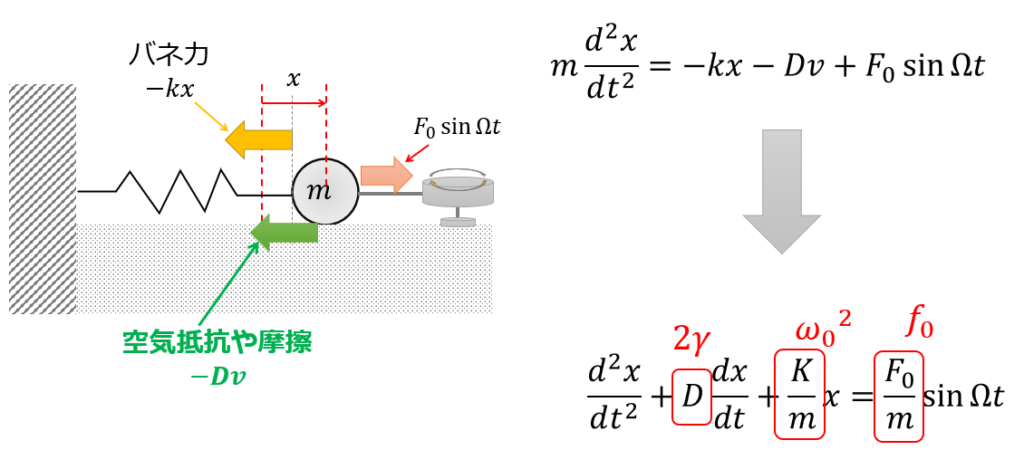
バネにつながれた質量\(m\)の質点が、速度に比例する抵抗（空気抵抗や摩擦）を受けている場合に加えて、振動数\(\Omega\)で周期的に力\(F_{0}\sin\Omega t\)が加わっている場合の運動方程式です。
※\(x\)は自然長からのバネの伸びです。

運動方程式

\begin{align*}
m\frac{d^2x}{dt^2}=-kx-D\frac{dx}{dt}+F_{0}\sin\Omega t \tag{2}
\end{align*}

となります。

そして、これを以下のように整理します。

\(\gamma=\frac{D}{2m}\)
\(\omega_{0}=\sqrt{\frac{k}{m}}\)
\(f_{0}=\frac{F_{0}}{m}\sin\Omega t\)

強制振動の運動方程式

\begin{align*}\ddot{x}+2\gamma\dot{x}+\omega_{0}^2 x=f_{0}\sin\Omega t\tag{3}\end{align*}

※\(\dot{x}=\frac{dx(t)}{dt}\)

※\(\ddot{x}=\frac{d^2x(t)}{dt^2}\)

本日、解く微分方程式は(3)です。

2階非斉次線形微分方程式とは何か

前回の記事では、「2階斉次線形微分方程式」についての話をしましたが、今回考える微分方程式は「2階非斉次線形微分方程式」です。

以下のにその特徴をまとめておきます。

最大の特徴は、右辺が０ではなく\(f(t)\)となっていることです。
右辺が0ではないだけで、ものすごくややこしくなる・・・ように感じるのですが、この手の微分方程式の解法は前回の記事の解法の応用を効かせるだけですのでそれほど難しくありません。

カマキリ

この記事を読めば慌てずに対処できるはずです！

2階非斉次線形微分方程式の解法

では、これから(3)の微分方程式を解くのですが・・・・もう一度式を書いておきます。

強制振動の運動方程式

\begin{align*}\ddot{x}+2\gamma\dot{x}+\omega_{0}^2 x=f_{0}\sin\Omega t\tag{3}\end{align*}

\(\gamma=\frac{D}{2m}\)
\(\omega_{0}=\sqrt{\frac{k}{m}}\)
\(f_{0}=\frac{F_{0}}{m}\sin\Omega t\)

解き方は定石というのがあります。

以下の「解法のフロー」を用意しました。

このフローにしたがって（何だったら何も考えずに）、計算を進めていけば良いです。
微分方程式を十分に習っていない状態であれば、機械的にこれにしたがってやりましょう！！

では、順番にやっていきましょう！

\(f_{0}=0\)の場合の一般解を求める

\(f_{0}=0\)についての微分方程式↓

\begin{align*}\ddot{x}+2\gamma\dot{x}+\omega_{0}^2 x=0\tag{4}\end{align*}

この微分方程式の解は、前回の記事で求めましたので結果だけ記載しておきます。

\begin{align*}
x(t)=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}\tag{4}
\end{align*}

\(A,B\)が積分定数です。
(3)は2階の微分を含む微分方程式ですので、(3)を2回積分して得られる解\(x(t)\)は必ず2つの積分定数が含まれています。

であれば、(4)で求めた一般解(7)を利用するのが上手い方法である・・・と考えるのが自然だと思います。

では、(3)の一般解を以下の形であると仮定します。

(3)の一般解

\begin{align*}
x(t)&=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}+C\sin\Omega t+D\cos\Omega t \\
&=x_{1}(t)+x_{2}(t)\tag{5}
\end{align*}

※(4)の一般解の項を\(x_{1}(t)=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}\)でまとめておきました。
※(3)の特殊解の項を\(x_{2}(t)=C\sin\Omega t+D\cos\Omega t\)でまとめておきました。

(3)の左辺は「(5)の\(x_{1}(t)\)で0になる」として、(3)の右辺を出すためには同じ振動数\(\Omega\)を使った周期関数を持ってくるのがセンスがいいんじゃないかって思いますよね。
しかも、積分定数はすでに2つ使っているので、これ以上積分定数を増やす必要もありません。

なので、注力すべきは「(5)が(3)を満たしてくれるように\(C,D\)を決定する」ということになります。

強制振動の特殊解\(x_{2}(t)\)を求める

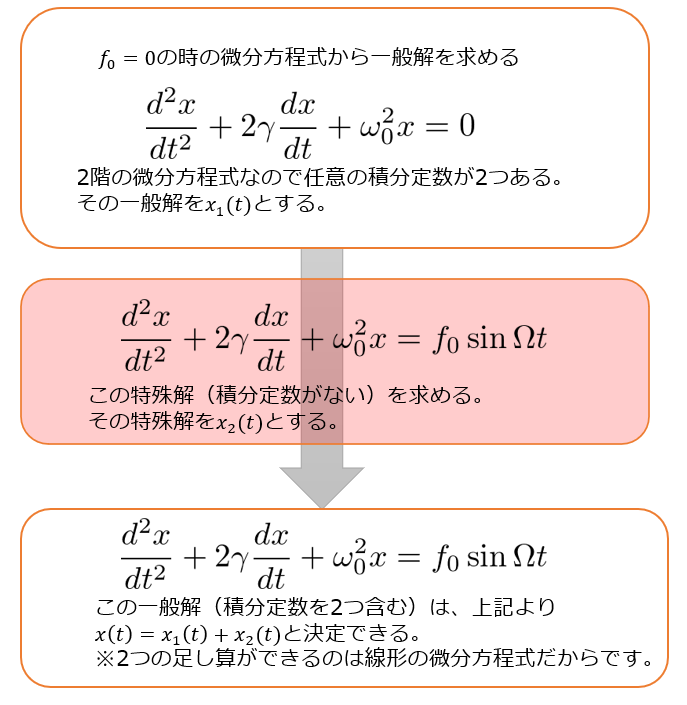
「(5)が(3)を満たすように\(C\)を決定すればよい」という言いましたが、少し急ぎすぎたかもしれません。

まず、(5)の一般解は「\(x(t)=x_{1}(t)+x_{2}(t)\)」と書きました。

\(x_{1}(t)\)は\(f_{0}=0\)での一般解
\(x_{2}(t)\)は(5)の特殊解（積分定数を含まない）」

ということを意識する必要があります。

だから、そもそも\(x_{1}(t)\)は以下を満たしているという事を頭に置いておかなくてはいけません。

\begin{align*}\ddot{x_{1}}+2\gamma\dot{x_{1}}+\omega_{0}^2 x_{1}=0\tag{6}\end{align*}

しつこいくらい強調しているのは、自分自身がはじめて強制振動を習ったときに十分理解していなかったので、全く何をやっているのか理解ができなかったからです。

では、\(x(t)=x_{1}(t)+x_{2}(t)\)を(5)に代入してみましょう。

\begin{align*}\big(\ddot{x_{1}}+2\gamma\dot{x_{1}}+\omega_{0}^2 x_{1}\big)+\big(\ddot{x_{2}}+2\gamma\dot{x_{2}}+\omega_{0}^2 x_{2}\big)=f_{0}\sin\Omega t\tag{7}\end{align*}

これより(6)を用いると、\(x_{1}\)が消えてくれます。

\begin{align*}
\ddot{x_{2}}+2\gamma\dot{x_{2}}+\omega_{0}^2 x_{2}=f_{0}\sin\Omega t\tag{8}
\end{align*}

となります。

なんだ全然さっきと微分方程式が変わってないじゃないかと思うかもしれませんが、ちょっと違います。

(8)の\(x_{2}(t)\)は、積分定数が必要ない特殊解で良いという事です。つまり、とりあえず(8)を満たしてくれるような解を探してこれば良いという事です。

となると、先ほども言ったように右辺が振動数\(\Omega\)の周期関数であるなら、特殊解も\(\Omega\)を持つ周期関数にしておくのがセンスが良いのではないかと考えますよね。

ならば、(8)の特殊解を、

\begin{align*}
x_{2}=C\sin\Omega t+D\cos\Omega t\tag{9}
\end{align*}

とおいてみてはどうかとなります。

こうすることで、ここでも目的がはっきりしてきます。

【ここでの目的】
(8)を満たすような特殊解を「\(x_{2}=C\sin\Omega t+D\cos\Omega t\)」と仮定して、(8)を満たしてくれるように\(C\)を定める。

目的は一言で言うと「\(C\)」を決めることですね。

では、(9)を(8)に代入してみましょう。

\begin{align*}
x_{2}=C\sin\Omega t+D\cos\Omega t\tag{9}
\end{align*}

(9)を微分したものを用意しておいて・・・

\(\frac{dx_{2}}{dt}=C\Omega\cos\Omega t-D\omega\sin\omega t\)
\(\frac{d^2x_{2}}{dt^2}=-C\omega^2\sin\Omega t-D\Omega^2\cos\Omega t\)

なので、(8)に代入すると、

\begin{align*}
&\bigg(-C\Omega^2\sin\Omega t-D\Omega^2\cos\Omega t\bigg)\\
&+2\gamma\bigg(C\Omega\cos\Omega-D\Omega\sin\Omega t\bigg)\\
&+\Omega_{0}^2\bigg(C\sin\Omega t+D\cos\Omega t\bigg)=f_{0}\sin\Omega t\tag{10}
\end{align*}

これを\(\sin,\cos\)にまとめて、

\begin{align*}
&\bigg(-C\Omega^2-2\gamma D\Omega+C\omega_{0}^2\bigg)\sin\Omega t\\
&+\bigg(-D\Omega^2+2\gamma C\Omega +\omega_{0}^2 D\bigg)\cos\omega t \\
&=f_{0}\sin\Omega t\tag{11}
\end{align*}

これより、

\(C=\frac{(-\omega^2+\omega_{0}^2)f_{0}}{(-\omega^2+\omega_{0}^2)^2+(2\gamma\omega)^2}\)
\(D=\frac{-\gamma\omega f_{0}}{(-\omega^2+\omega_{0}^2)^2+(2\gamma\omega)^2}\)

\(C,D\)を計算する方法として中には、\(C\)と\(D\)の連立方程式を愚直に計算した人もいることでしょう。
その計算方法は個々人の方法で良いかと思いますが、今回の場合は行列計算を考える方が手っ取り早いですし、ミスが少ないと思いますので少し紹介をしておきます。

まず、\(\sin\)と\(\cos\)の係数が両辺で等しいとし、\(C\)と\(D\)については以下のように連立方程式が解きやすいように整理します。

\begin{align*}
\left\{\begin{matrix}
\big(-\Omega^2+\omega_{0}^{2}\big)C-2\gamma\Omega D=f_{0}\\
2\gamma\Omega C+\big(-\Omega^2+\omega_{0}^{2}\big)D=0
\end{matrix}\right.
\end{align*}

これを行列になおします。

\begin{align*}
\begin{pmatrix}
-\Omega^2+\omega_{0}^{2} & -2\gamma\Omega\\
2\gamma\Omega & -\Omega^2+\omega_{0}^{2}
\end{pmatrix}
\begin{pmatrix}
C \\
D
\end{pmatrix}=
\begin{pmatrix}
f_{0} \\
0
\end{pmatrix}
\end{align*}

2行2列の行列計算は以下のように簡単に行えます。

\begin{align*}
\begin{pmatrix}
C \\
D
\end{pmatrix}=
\frac{1}{\big(-\Omega^2+\omega_{0}^2\big)^2+\big(2\gamma\Omega\big)^2}
\begin{pmatrix}
-\Omega^2+\omega_{0}^{2} & 2\gamma\Omega\\
-2\gamma\Omega & -\Omega^2+\omega_{0}^{2}
\end{pmatrix}
\begin{pmatrix}
f_{0} \\
0
\end{pmatrix}
\end{align*}

これより、\(C,D\)が求まります。

\(C=\frac{(-\Omega^2+\omega_{0}^2)f_{0}}{(-\Omega^2+\omega_{0}^2)^2+(2\gamma\Omega)^2}\)
\(D=\frac{-2\gamma\Omega f_{0}}{(-\Omega^2+\omega_{0}^2)^2+(2\gamma\Omega)^2}\)

カマキリ

この方法なら簡単にC,Dが求めることができます。

2階非斉次線形微分方程式の一般解は？

以上のような流れを確認しつつ、(3)の一般解を求めることができました。

(3)の一般解

\begin{align*}
x(t)=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}+C\sin\Omega t+D\cos\Omega t \tag{12}
\end{align*}

※(4)の一般解の項を\(x_{1}(t)\)でまとめておきました。
※(3)の特殊解の項を\(x_{2}(t)\)でまとめておきました。

\(C=\frac{(-\Omega^2+\omega_{0}^2)f_{0}}{(-\Omega^2+\omega_{0}^2)^2+(2\gamma\Omega)^2}\)
\(D=\frac{-2\gamma\Omega f_{0}}{(-\Omega^2+\omega_{0}^2)^2+(2\gamma\Omega)^2}\)

\(C,D\)は代入せずに別で記述しておきました。

代入して書くと、

\begin{align*}
x(t)&=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}\\
&+\frac{(-\omega^2+\omega_{0}^2)f_{0}}{(-\omega^2+\omega_{0}^2)^2+(2\gamma\omega)^2}\sin\Omega t\\
&+\frac{-2\gamma\omega f_{0}}{(-\omega^2+\omega_{0}^2)^2+(2\gamma\omega)^2}\cos\Omega t \tag{13}
\end{align*}

↑めちゃくちゃごちゃごちゃしてますね。

(13)が本当に(3)の一般解になっているのか、(3)の左辺に代入して確認してみてください。
ちゃんと満たしていることが確認できます。

まとめ

今回は「2階非斉次線形微分方程式」の解法について解説をしました。

まず、以下のフローを今一度確認しておきましょう！

(3)の一般解

\begin{align*}
x(t)=A e^{(-\gamma+\sqrt{\gamma^2-\omega_{0}^2})t}+B e^{(-\gamma-\sqrt{\gamma^2-\omega_{0}^2})t}+C\sin\Omega t+D\cos\Omega t \tag{12}
\end{align*}

※(4)の一般解の項を\(x_{1}(t)\)でまとめておきました。
※(3)の特殊解の項を\(x_{2}(t)\)でまとめておきました。

\(C=\frac{(-\Omega^2+\omega_{0}^2)f_{0}}{(-\Omega^2+\omega_{0}^2)^2+(2\gamma\Omega)^2}\)
\(D=\frac{-2\gamma\Omega f_{0}}{(-\Omega^2+\omega_{0}^2)^2+(2\gamma\Omega)^2}\)

内容は以上となります。

この「2階非斉次線形微分方程式」は大学一年生の力学で一番初めに習う微分方程式だと思います。

大学院試験やレポート問題でも最頻出のひとつですので必ずマスターしておきましょう(^^)/