こんにちは(@t_kun_kamakiri)(^^)/
前回では連立方程式を解くための公式であるクラメルの公式とその演習問題について解説を行いました。
クラメルの公式は手計算で3つの連立方程式を解く際には有効な手段ではありますが、4つの連立方程式を解く際にはちょっと無理がある解法です。
なぜなら3つの連立方程式をクラメルの公式を用いて解く際には、3次正方行列の行列式を計算する必要があるからです。
3次の正方行列までならサラスの公式を使うことで行列式を簡単に手計算でも求めることができますが、4次の正方行列だとそうはいきません。
ましてや、数値計算をしようものなら1000つ程度の連立方程式を解く必要があったり、1000×1000の規模の大きさの行列を取り扱います。
そこで大規模な連立方程式を数値計算で解く際にも使われるのがこちら。
掃き出し法
今回は掃き出し法について紹介します。
簡単な例題を用いて身に付けましょう(^^)/
次の連立方程式の解$x_{1},x_{2},x_{3}$を掃き出し法を使って求めます。
\left\{\begin{matrix}
3x_{1}+2x_{2}+x_{3}&=&1\\
2x_{1}+2x_{2}+x_{3}&=&5\\
x_{1}+3x_{2}+2x_{3}&=&2
\end{matrix}\right.\tag{1}
\end{align*}
これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。
- 行列をはじめて習う高校生・大学生
- 仕事で行列を使うけど忘れてしまった社会人
この記事の内容をマスターして行列計算を楽に計算できるようになりましょう(^^)
拡大係数行列
今回解く問題はこちらですね。
\left\{\begin{matrix}
3x_{1}+2x_{2}+x_{3}&=&1\\
2x_{1}+2x_{2}+x_{3}&=&5\\
x_{1}+3x_{2}+2x_{3}&=&2
\end{matrix}\right.\tag{1}
\end{align*}
まずは連立方程式を行列に書きなおしてやりましょう。
\underset{A}{\begin{pmatrix}
3 &2 &1 \\
2 & 2 &1 \\
1 & 3 &2
\end{pmatrix}}
\underset{X}{\begin{pmatrix}
x_{1} \\
x_{2} \\
x_{3}
\end{pmatrix}}
=\underset{B}{\begin{pmatrix}
1 \\
5 \\
2
\end{pmatrix}}\tag{2}
\end{align*}
このように行列にすれば$AX=B$の$X$を求めればよいのがわかりますね。
$A$が3行3列の行列、$B$が3行1列の行列です。
ここで表記上の話ですが、(2)の$X$を除いて左辺の行列$A$と右辺の行列$B$を以下のように表記します。
係数だけを並べて、行列$A$と行列$B$拡大した行列なので拡大係数行列と言います。
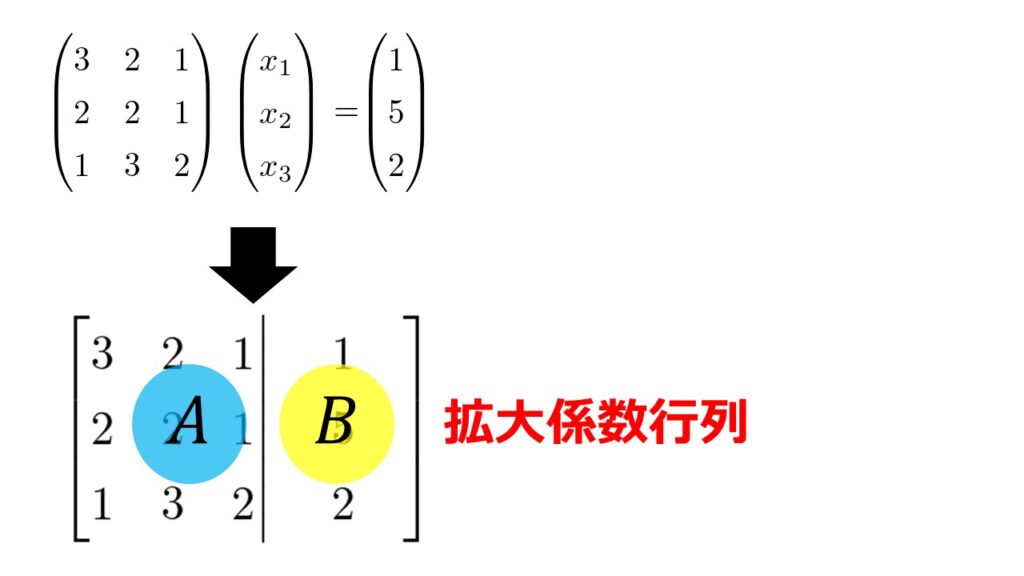
このように書いておくと掃き出し法で連立方程式を解く際には便利なのですね。
以下にこの$\left [\begin{matrix}
3 &2 &1\\
2 & 2 &1\\
1 & 3 &2
\end{matrix}\right|
\left.\begin{matrix}
1\\
5\\
2
\end{matrix}\right]$の表記を扱うかが本記事の内容となります。
どのように便利かを体験するために、まずは拡大係数行列の記法を使わずに掃き出し法で連立方程式を解いてみましょう。
拡大係数行列を使わずに掃き出し法で解く
ここで連立方程式を解く方法は、あくまで掃き出し法です。
\left\{\begin{matrix}
3x_{1}+2x_{2}+x_{3}&=&1\\
2x_{1}+2x_{2}+x_{3}&=&5\\
x_{1}+3x_{2}+2x_{3}&=&2
\end{matrix}\right.\tag{1}
\end{align*}
ここで解説するステップを踏むことで比較的簡単に連立方程式を解くことができます。
Step1:上から下へ掃き出していく
まずは変数をどんどん消していく作業をします。
上の式を使って下の式の変数を消去していきます。
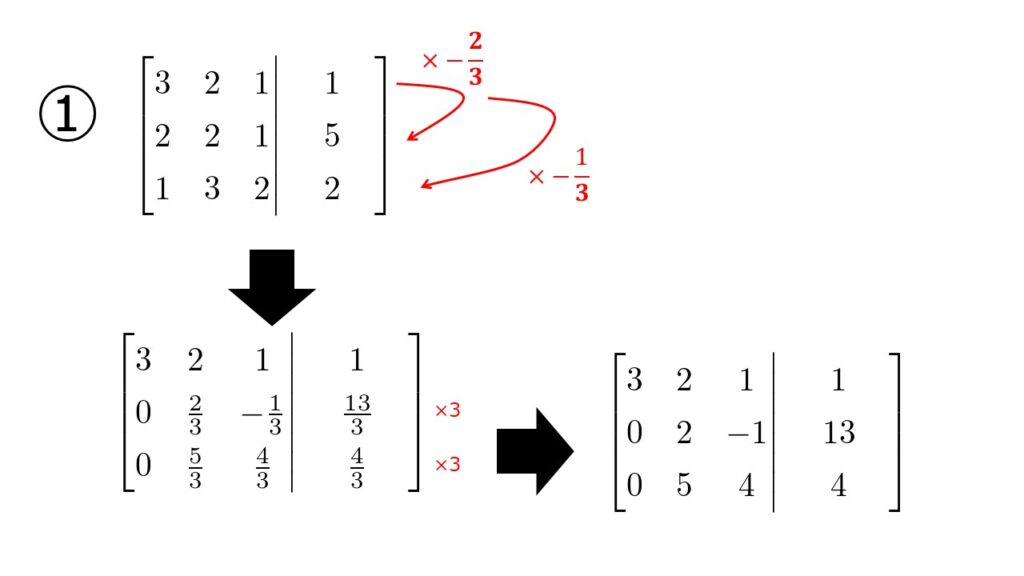
①について
- 1つ目の式を$-\frac{2}{3}$をかけて2つ目の式に足す
- 1つ目の式を$-\frac{1}{3}$をかけて3つ目の式に足す
- 2つ目と3つ目のしきを$3$倍する

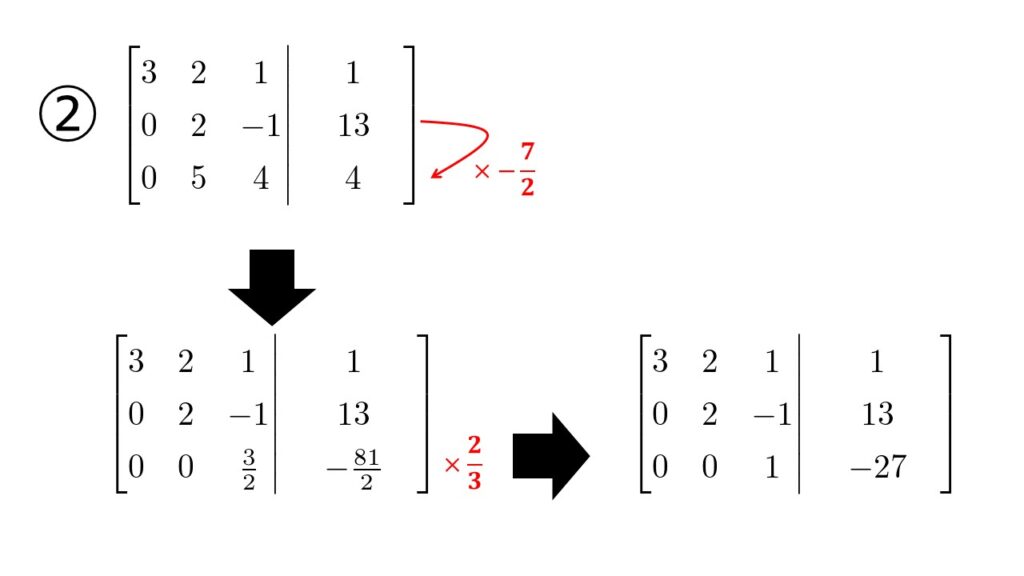
②について
できた式に以下の操作を行います。
- 2つ目の式を$-\frac{7}{2}$倍して3つ目の式に足す
- 3つ目の式を$\frac{2}{3}$倍して$x_{3}$を求める

以上で上から下へ引き算を行って$x_{3}=-27$が求まります。
Step2:下から上に掃き出していく
今度は下の式を使って上の式の変数を消去していきます。
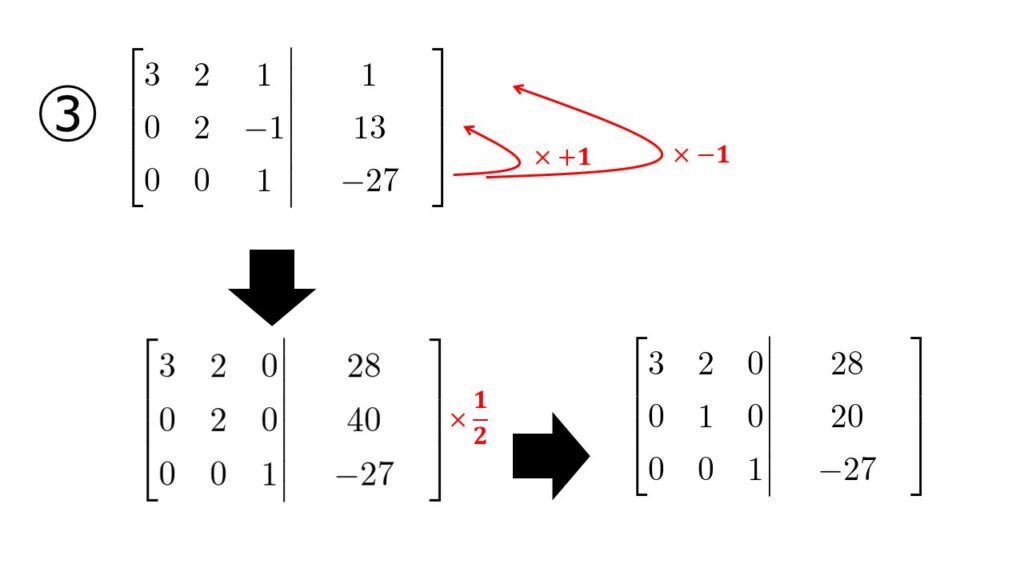
③について
- 3つ目の式を$+1$かけて2つ目の式に足す
- 3つ目の式を$-1$かけて1つ目の式に足す


2つ目の式の両辺を$\frac{1}{2}$倍することで$x_{2}=20$と求まります。
④について
- 2つ目の式を$-1$かけて1つ目の式に足して$x_{2}$を消去する
- 1つ目の式を$\frac{1}{3}$をかける$x_{1}=-4$と求まる


以上のステップを踏むと、
\left\{\begin{matrix}
&x_{1}&&&=&-4\\
&&x_{2}&&=&20\\
&&&x_{3}&=&-27
\end{matrix}\right.
\end{align*}
今回は計算をしてみて「$x_{1},x_{2},x_{3}$の係数のみ計算しているのだから、$x_{1},x_{2},x_{3}$とわざわざ書くのが面倒だな」って思ったことでしょう。
そこで、$x_{1},x_{2},x_{3}$を書かずに上記の計算を行える記法が拡大係数行列です。
拡大係数行列を使って連立方程式を解く
では、先ほどの問題を拡大係数行列を使ってやってみましょう。
最終目標は拡大係数行列の左側を対角成分がのみが1になる単位行列$E$にすることです。
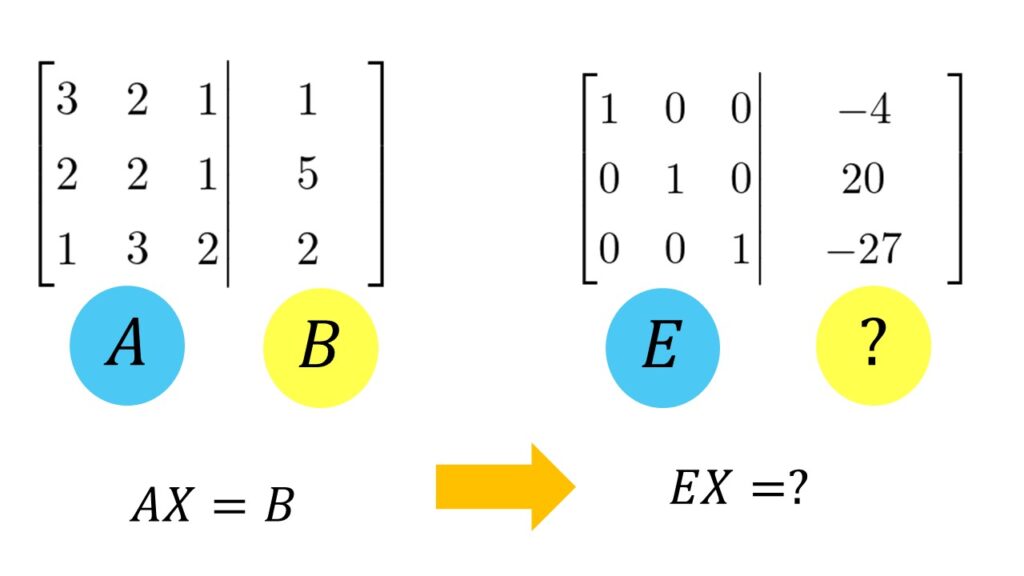

拡大係数行列で変形していった最後の「?」の部分はどうなるでしょうか?
計算を進めながら考えてみましょう。
では、やってみましょう。





拡大係数行列を使うと$x_{1},x_{2},x_{3}$を書かない分すっきりと計算を進めることができますね。
結果をまとめておくと以下の3つの表記は異なりますが意味は同じです。
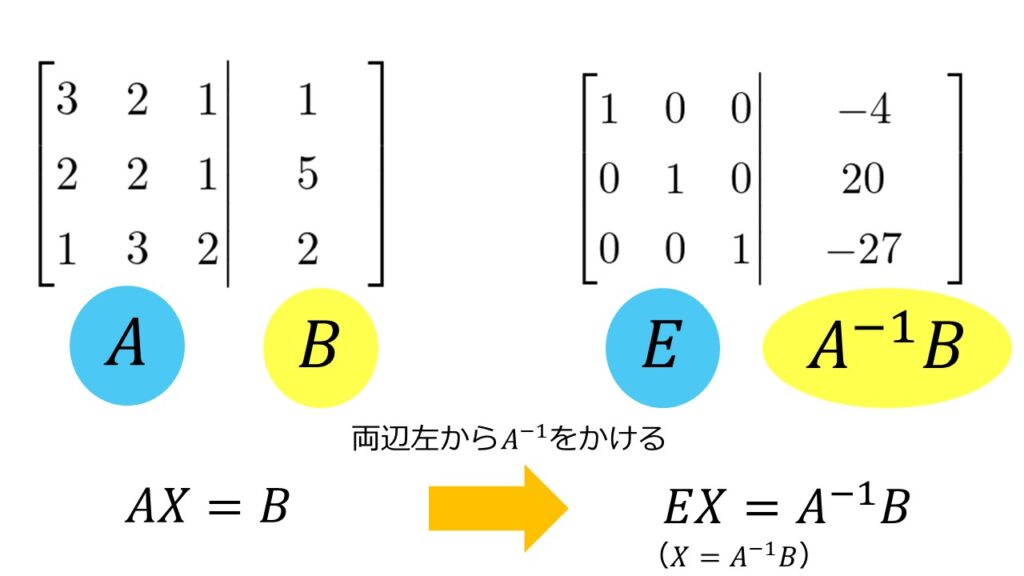
まとめ
今回は拡大係数行列を使って掃き出し法で連立方程式を解きました。
手計算の上でも、数値計算を行う上でも変数が多い場合(もっと大きな行列計算が必要な場合)でも掃き出し法はとても有効な手段ですので是非練習しておきましょう。
参考にする参考書はこれ
当ブログでは、以下の2つの参考書を読みながらよく使う内容をかいつまんで、一通り勉強すればついていけるような内容を目指していこうと思います。
大事なところをかいつまんで、「これはよく使うよな。これを理解するためには補足で説明をする」という調子で進めていきます(^^)/










