少しづつ「ランダウ=リフシッツの”力学”」を読み進めております(笑)
P.15の「第2章:保存法則」をやっていこうと思います。
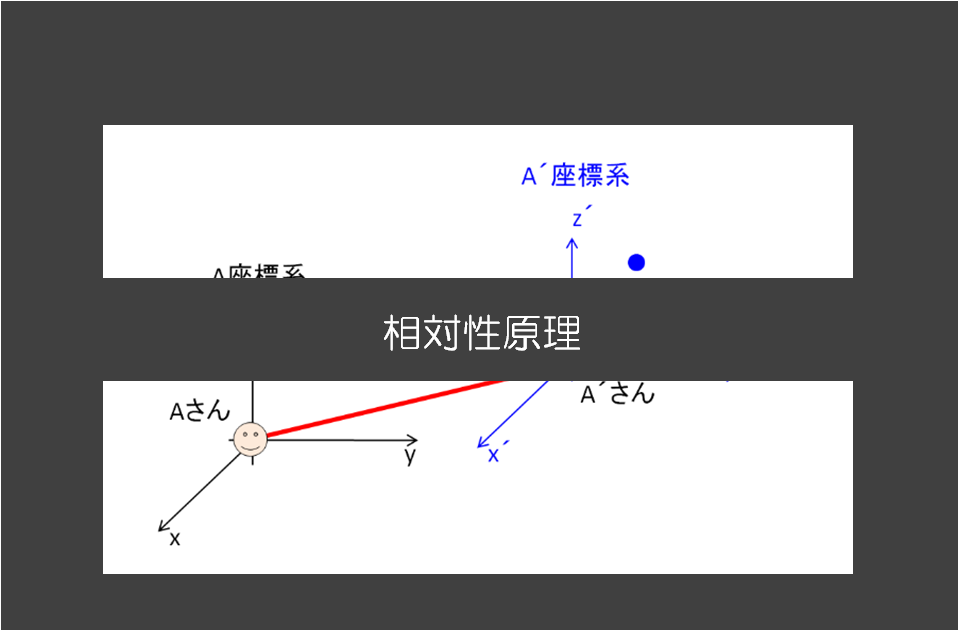
ここで重要な考え方は、
「対称性があると保存則があるよ」という意味です。
これは一般的にはネーターの定理と呼ばれるもので、大きな枠で捉えることができると考えています(^^)
ネーターの定理
「系に連続的な対称性がある場合はそれに対応する保存則が存在する」と述べる定理である。
ドイツの数学者エミー・ネーターによって1915年に証明され、1918年に公表された。
解析力学や場の理論における重要な定理であります。
これだけ覚えておけば良いでしょう(^^)/
「対称性が何によるかによって保存則が決まっている」という理解です。
| 対称性 | 保存則 |
| 時間対称性 | エネルギー保存則 |
| 並進対称性 | 運動量保存則 |
| 回転対称性 | 角運動量保存則(モーメントの保存) |
| ゲージ対称性(位相変換) | 電荷保存則 |
ざっと思いつくのはこんなとこでしょうか。(もっとあるですが、ここではこのくらいに・・・)
ですので、ネーターの定理を頭に置きつつ解析力学の枠内で、
「エネルギー」「運動量」「角運動量」などをラグランジアン\(L\)で記述していけば良いということになるのですね。
まず、エネルギーから見ていきましょう(^^)/
時間対称性(時間一様性)⇔エネルギー保存則
さて、
時間一様性ということは、ラグランジアン\(L\)が時間\(t\)にあらわに依存していないということを意味していますのでラグランジアン\(L\)は
このようになり、ラグランジアンの全微分は、
となりますね。
↓全微分についてはこちらを参考ください(^^)/
(2)式をdtで割って、時間の変化量を見てみましょう。
⇔
ここで注意なのですが、(3)式の\(L\)が時間にあらわに依存しないからといって、\(\frac{dL}{dt}=0\)というわけではないです。
(3)式は、時間\(t\)が変わることで座標\(q_{i}\)と速度\(\dot{q}_{i}\)が変わるのでラグランジアン\(L\)も変わると言ってることになります。
(3)式の\(L\)が時間にあらわに依存しないという意味は、座標\(q_{i}\)と速度\(\dot{q}_{i}\)が固定された状態では時間変化しない、すなわち偏微分が0(\(\frac{\partial L}{\partial t}=0\))という意味になります。
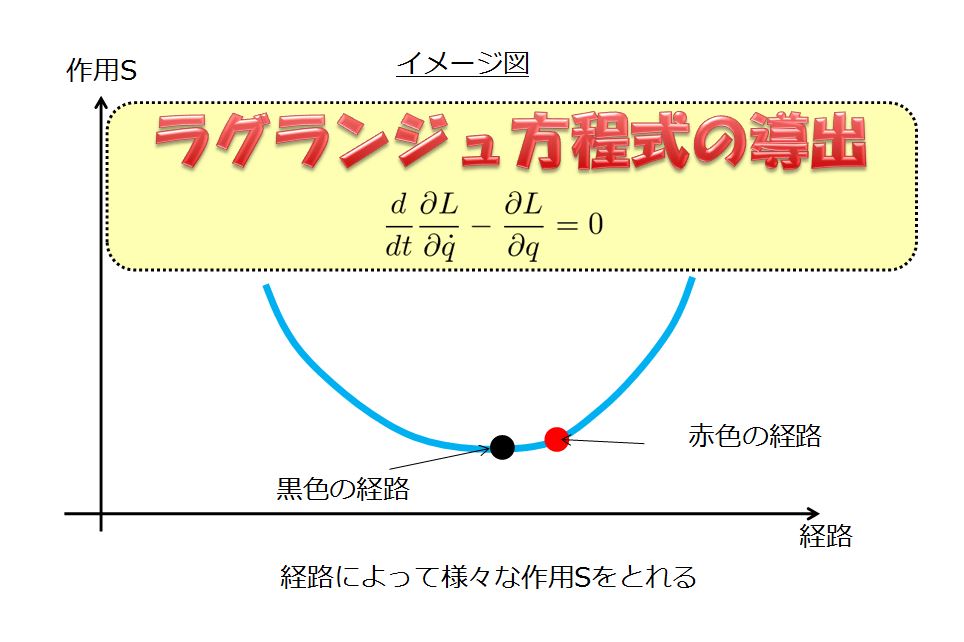
(3)式の第一項に、ラグランジュ方程式\(\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_{i}}=\frac{\partial L}{\partial q_{i}}\)を使うと、
よく見ると(4)式の右辺がうまいこと、
(右辺)=\(\sum_{i}\frac{d}{dt}\bigg(\frac{\partial L}{\partial \dot{q}_{i}}\dot{q}_{i}\bigg)\)
とできるので、(4)式は、
左辺を右辺に移行すれば、
という感じになりましたね!(^^)!
といったん\(E\)という文字で置いておきます。
(7)式をエネルギーと呼びます。
なんともよそよそしく「エネルギー」と呼びましたが(笑)
ここまでは、あくまで(7)式のように置くと、
と表しただけで(7)式がエネルギーかどうかよくわからないからよそよそしく「エネルギー」と言っておく感じです。
では、(7)式がよく知っているエネルギーの形になっているのかを確認すれば、自信を持って(7)式がエネルギーと呼ぶことができるので、それを見ていこうと思います。
(7)式がエネルギーの形になっているのか確認
確認しましょう(^^)/
ラグランジアン\(L\)は、外力などが保存力\(\bf{F}=-\nabla U\)であれば次のように書けたのでしたね。
T:運動エネルギー
U:ポテンシャルエネルギー
(9)式を具体的に座標と速度で依存しているという感じに書いておきましょう。
もっと具体的にそれぞれが何に依存しているかを明確にして書いておきましょうか。
ポテンシャルエネルギー\(U\)は座標にしか依存しないですし、運動エネルギー\(T\)は速度にしか依存しません。
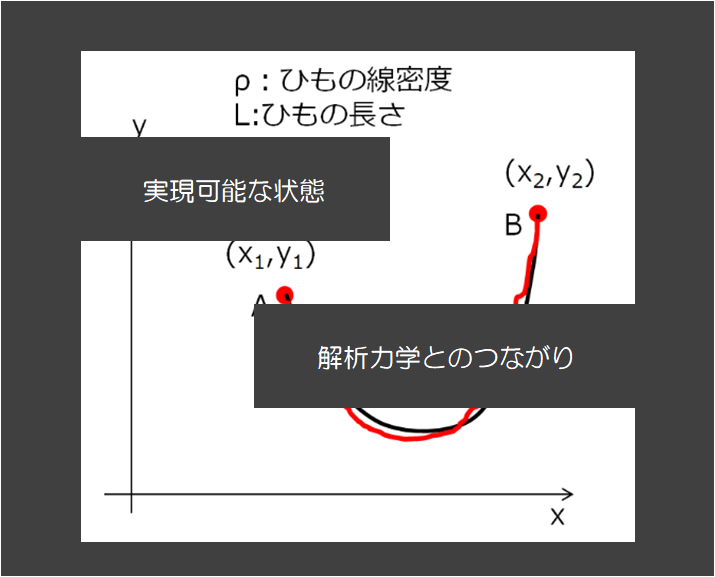
運動エネルギーに関していえば、最小作用の原理より速度の2乗のような形にしか依存しないということも下記の記事で述べました。
ゆえに、(7)式の第一項は簡単に計算できて、
(12)式の計算途中も記載しましょう(^^)/
↓こんな感じです。

なので(7)式は、
⇔
エネルギーの形になりましたね!(^^)!
ということは(8)式の、
これはエネルギー保存則(エネルギーは時間に対して一定)を意味しているということになりますね。
まとめ
時間対称性(時間一様性)とすると、エネルギー保存則が成り立つ。
\begin{align*}\frac{dE}{dt}=0\cdot\cdot\cdot (8)\end{align*}
ただし\(E\)は、
\begin{align*}E=\sum_{i}\frac{\partial L}{\partial \dot{q}_{i}}\dot{q}_{i}-L\cdot\cdot\cdot (7)\end{align*}
と表す。
\(E\)をエネルギーと呼びます。
次回
次回は、「並進対称性(空間一様性)」から「運動量保存」を見てみましょう(^^)/
参考図書
いくつかおすすめの解析力学の参考書を挙げておきます。
ランダウ力学
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
その方が書いた書籍なので高校生でも読みこなすことができるくらいわかりやすく、かつちゃんと大学の物理の内容を扱っています。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
数学的な解説も多く、解析力学を深く学ぶ人には挑戦するには申し分ない内容です。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。




























≪対称性があると保存則があるよ≫は、
系に連続的な対称性(双対性)のエミー・ネーターの数学版と観照しよう。
縮約(縮退)自然数と見る自然数【0 1 2 3 ・ ・ ・ 】が、【数である】事としてくれた「数学の現象学」的思考の【離散数学】から【連続数学】への『落とし込み』として見てとれる数理哲学としての作用素〔0 1 ∞〕から十進法の西洋数学の成果(e i π)のカオス表示で見てとれる。
カオス表示の一次元・二次元・三次元・四次元は、それぞれにカオス表示の積のヒエラルキーの表情を持つと見る。
三次元はジャーゴン(数の核)で四次元は【形態空間】の【容量】と【ホログラフィック係数】とで保存されると見る。
『離散的有理数の組み合わせの多変数創発関数論 命題Ⅰ 命題Ⅱ』の帰結の観照
【離散数学】 【連続数学】 数体の保存則
孵化係数 創発係数 カオス表示の保存則
有理数 実数 1/eのマルコフ過程
一次元と二次元の連続性 ゼータ関数の -1/12
ガンマ関数の √2π
と「数論幾何学」的に自然数と西洋数学の成果(e i π)とがラングランズ対応・双対と見
える。