こんにちは(@t_kun_kamakiri)(^^)/
「全微分と偏微分は説明できるでしょうか?」
全微分と偏微分の違いを視覚的に理解しておく
微分すらあやしいって方は以下の記事を参考にしてください!
では、解説をしていきます。
全微分
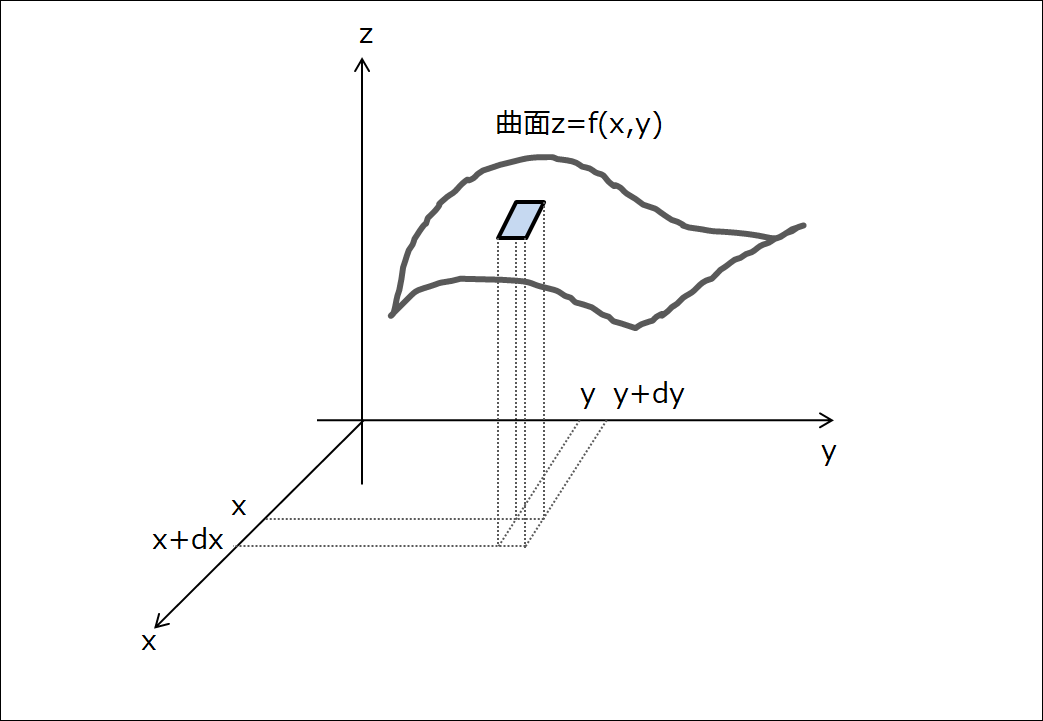
以下のような滑らかな曲面\(z=f(x,y)\)を考えましょう。
※滑らかと言っているのは、微分可能という意味で使っています。

さて、全微分はこの場合は、
を意味しますね。
つまり上の絵の①+②のことです。
二つの方法で(1)を見ていきましょう(^^)/
方法1:①と②をひとつずつ見て和をとる
①について
&=\lim_{dx \to 0}\frac{f(x+dx,y)-f(x,y)}{dx}dx\\
&=\frac{\partial f(x,y)}{\partial x}dx\tag{2}\end{align*}
②について
&=\lim_{dy \to 0}\frac{f(x,y+dy)-f(x,y)}{dy}dy\\
&=\frac{\partial f(x,y)}{\partial y}dy\tag{3}\end{align*}
よって\(df\)は、
&=f(x+dx,y+dy)-f(x,y)\\
&=f(x+dx,y)-f(x,y)+f(x,y+dy)-f(x,y)\\
&=\lim_{dx \to 0}\frac{f(x+dx,y)-f(x,y)}{dx}dx + \lim_{dy \to 0}\frac{f(x,y+dy)-f(x,y)}{dy}dy\\
&=\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy\tag{4}\end{align*}
これが全微分ですね(^^)
方法2:\(-f(x,y+dy)+f(x,y+dy)\)を加える
(1)式の\(df=f(x+dx,y+dy)-f(x,y)\)より、
&=\bigg(f(x+dx,y+dy)-f(x,y+dy)\bigg)+\bigg(f(x+dx,y+dy)-f(x,y)\bigg)\\
&=\lim_{dx \to 0}\frac{f(x+dx,y+dy)-f(x,y+dy)}{dx}dx+\lim_{dy \to 0}\frac{f(x,y+dy)-f(x,y)}{dy}dy\\
&=\frac{\partial f(x,y)}{\partial x}dx+\frac{\partial f(x,y)}{\partial y}dy\end{align*}
となります。
※3つ目の式は$\lim_{dx \to 0}\frac{f(x+dx,y+dy)-f(x,y+dy)}{dx}dx$について$y$については変化をさせていないので、$\lim_{dx \to 0}\frac{f(x+dx)-f(x)}{dx}dx=\frac{\partial f(x,y)}{\partial x}dx$と見るとわかりやすいですね。
ゆえに、
方法1同様、これが全微分ですね。
\(x\)に対する導関数\(\frac{df}{dx}\)と偏微分\(\frac{\partial f}{\partial x}\)の違い
ところで、微分\(\frac{df}{dx}\)と偏微分\(\frac{\partial f}{\partial x}\)の違いって視覚的にどう違うのか見てみましょう。
\(x\)に対する導関数\(\frac{df}{dx}\)の場合
これを絵で書くと水色ラインということですね(^^)
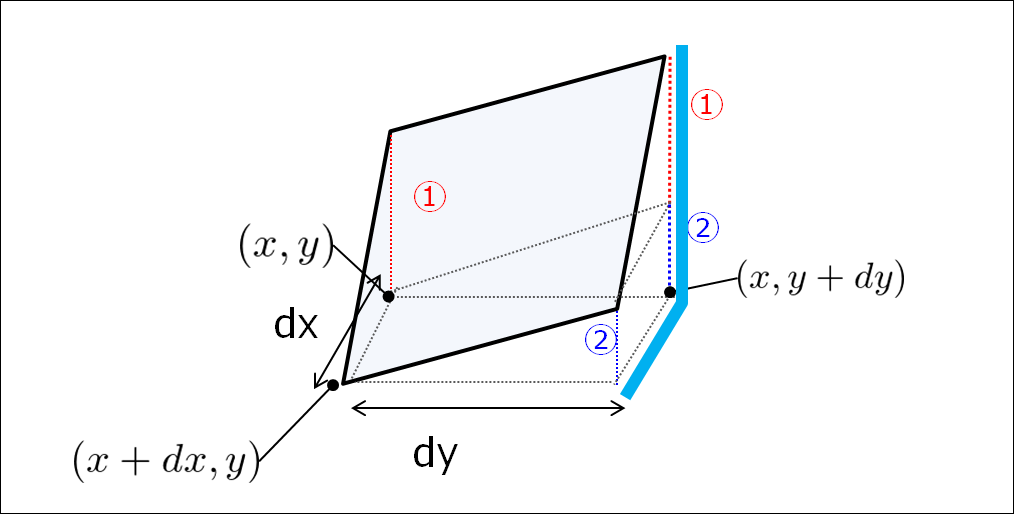
(4)式を\(dx\)で割ると、
式の上ではこのようになります。
\(x\)に対する偏微分\(\frac{\partial f}{\partial x}\)の場合
これを絵で書くと水色ラインということですね(^^)
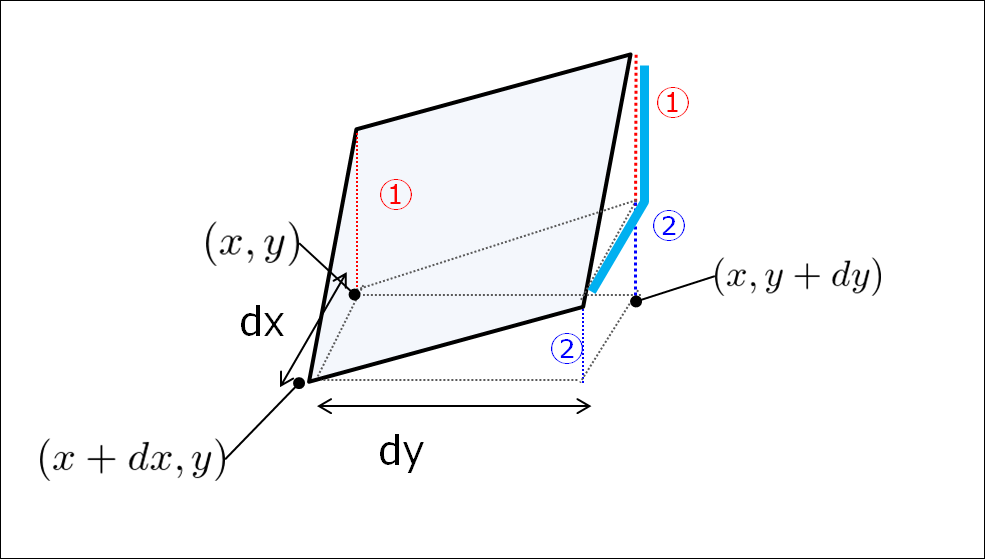
これは(4)式を使うのではなく、たんに\(y\)を固定したときの\(f(x,y)\)の変化量なので、
と書きます。
これを偏微分といいますね。
まとめ
数学的な厳密差には欠ける部分がありますが、視覚的なイメージで全微分や偏微分について解説を行いました。
全微分\(df\)の場合
微分\(\frac{df}{dx}\)の場合
偏微分\(\frac{\partial f}{\partial x}\)の場合
\(y\)を固定したときの\(f(x,y)\)の変化量
おすすめの参考書
最後におすすめの参考書を紹介しておきましょう。
マセマの参考書は大学初学年や、なんだったら高校生でも読めるくらいわかりやすく書かれていますので、「大学数学はキツイな」って感じた方は手に取ってみてください。




























[…] 全微分と偏微分の違いを視覚的に理解しておく […]