Step3:流速Uの値の設定
続いて流速であるUの値の設定を行いましょう。
以下の2つのファイルを作成します。
- Fields.h(ヘッダーファイル):変数、関数定義
- Fields.cpp:関数処理
Uは$u(x)$と関数として定義するため、$x$座標と座標に応じた$u$の値を持つようにします。Fields.h(ヘッダーファイル)を以下のようにします。
Fields.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
#ifndef FIELDS_H #define FIELDS_H #include "Mesh.h" #include <vector> using std::vector; class Fields { public: Fields();//constructor virtual ~Fields(); //deconstructor typedef vector<Fields> vectorField1d; double x1d; //x座標 double value; //Uの値 //vector<Fields> passGridinfomation(vector<Fields>&, Mesh&); Fields::vectorField1d passGridinfomation(Fields::vectorField1d&, vector<double>&); }; #endif //FIELDS_H |
vector<Fields>というvectorコンテナを使ってFieldsクラスの配列要素を作ります。
vector<Fields>と毎回書くのは煩雑になるので、以下のように名前を付けて定義しなおします。
|
1 |
typedef vector<Fields> vectorField1d; |
これにより「vector<Fields>」と書かずとも「vectorField1d」と書くだけで済みます。
Fields.cppに関数処理を書きます。
Fields.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include "Fields.h" #include <iostream> Fields::Fields(): x1d(0.0), value(2.0) { } Fields::vectorField1d Fields::passGridinfomation(Fields::vectorField1d& vec, vector<double>& xpts_) { /* typedef vector<Fields> vectorField1d; double value; double x1d; */ for (int i = 0; i < vec.size(); i++) { vec[i].x1d = xpts_[i]; } return vec; } Fields::~Fields() { std::cout << "Fields::~Fields() destructor" << std::endl; } |
肝になるところは以下の部分です。
|
1 2 3 4 |
Fields::vectorField1d Fields::passGridinfomation(Fields::vectorField1d& vec, vector<double>& xpts_) { (省略) } |
関数処理により返す型は「Fields::vectorField1d(FieldsクラスのvectorField1d)」です。「vectorField1d」は先ほど「vector<Fields>」と定義しなおしたので、Fieldsクラスを持った配列を返すようにしています。
main.cppでFieldsクラスのインスタンス化を行います。
※余分な記述は「/* */」で挟んでコメントアウトしました。
main.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
#include <iostream> #include <vector> #include "Mesh.h" #include "Fields.h"//add using namespace std; using std::vector; int main() { int Nx =10; double totallength = 2.0; Mesh mesh_(Nx, totallength);//Meshクラスのインスタンス化 /* cout << "mesh_.NumberOfNode = " << mesh_.NumberOfNode << endl; cout << "mesh_.lengthx = " << mesh_.lengthx << endl; cout << "mesh_.dx1d = " << mesh_.dx1d << endl; */ for (int i = 0; i < mesh_.xpts.size();i++) { cout << "xpts[" << i << "] = " << mesh_.xpts[i] << endl; } // UFields Fields FieldsOperations; cout << "UFieldsvec = " << FieldsOperations.value << endl; Fields::vectorField1d U(mesh_.NumberOfNode); // typedef vector<Fields> vectorField1d; U = FieldsOperations.passGridinfomation(U, mesh_.xpts); for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].x1d = " << U[i].x1d << endl; } for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].value = " << U[i].value << endl; } return 0; } |
「Fields FieldsOperations;」でクラスのインスタンス化を行っています。
Fields.cppで以下のように初期化されていることに注意です。
|
1 2 3 4 5 |
Fields::Fields(): x1d(0.0), value(2.0) { } |
ですので、「FieldsOperations.value」はFieldsクラス内の初期値として2.0が出力されます。
|
1 |
vector<Fields> UFieldsvec(5); |
は一見わかりにくいですが、要素数5つのFieldsクラスを持った配列を定義しています。
「vector<double>」は要素がdouble型の数値ですが、「vector<Fields>」は要素がFields型のクラスです。
値の出力にはクラス内のメンバ変数にアクセスする必要があるため、
|
1 2 3 4 |
for (int i = 0; i < UFieldsvec.size(); i++) { cout << "UFieldsvec[" << i << "] = " << UFieldsvec[i].value << endl; } |
のように、まず「UFieldsvec[i]」として配列の一つを取り出して「.(ドット)」でメンバ変数にアクセスします。
|
1 |
U = FieldsOperations.passGridinfomation(U, mesh_.xpts); |
で、「FieldsクラスのvectorField1dのU」と「vector<double>型のmesh_.xpts」を引数にしています。
【結果】
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
Mesh::Mesh xpts[0] = 0 xpts[1] = 0.222222 xpts[2] = 0.444444 xpts[3] = 0.666667 xpts[4] = 0.888889 xpts[5] = 1.11111 xpts[6] = 1.33333 xpts[7] = 1.55556 xpts[8] = 1.77778 xpts[9] = 2 UFieldsvec = 2 Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor U[0].x1d = 0 U[1].x1d = 0.222222 U[2].x1d = 0.444444 U[3].x1d = 0.666667 U[4].x1d = 0.888889 U[5].x1d = 1.11111 U[6].x1d = 1.33333 U[7].x1d = 1.55556 U[8].x1d = 1.77778 U[9].x1d = 2 U[0].value = 2 U[1].value = 2 U[2].value = 2 U[3].value = 2 U[4].value = 2 U[5].value = 2 U[6].value = 2 U[7].value = 2 U[8].value = 2 U[9].value = 2 Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Mesh::~Mesh() deconstructor |
これにて「U[i].x1d」でx座標を、「U[i].value」でUの値を格納することができました。
※「Fields::~Fields() destructor」はFieldsクラスを抜けるたびにメモリ解放のために動作するデストラクタです。勉強のためデストラクタがいつのタイミングで作動したかを出力しています。
Step4:演算子のオーバーロード
+や-の演算子は数値や文字列など特定のデータ型にしか使うことができないです。
例えば、
|
1 2 3 4 5 6 7 |
int int_a; int int_b; int_b = int_a + 4; double double a; double double b; double b = double a + 4; |
などの演算は可能ですが、クラスから生成されたオブジェクト同士の演算はすることができません。
|
1 2 3 4 5 |
Fields U; Fields V; Fields W; W = U + V; //error |
もし仮に、上記のようなユーザー定義のクラスに対して演算を行うことができれば直感的なプログラムを構築することができます。その際に、演算子のオーバーロードを使います。演算子のオーバーロードはクラスでメンバ関数として定義します。ここで用いるのが operator キーワードです。
まずは、演算子のオーバーロードの理解のためにFields.hにoperator+関数を定義します。
Fields.h(主要部分のみ)
|
1 2 |
//演算子のオーバーロード Fields operator+(const Fields&); |
Fields.cppで関数の処理内容を書きます。
Fields.cpp(主要部分のみ)
|
1 2 3 4 5 6 7 |
Fields Fields::operator+(const Fields& vecA) { Fields temp; temp.value = value + vecA.value;//this->value + vecA.value return temp; } |
引数としてFieldsクラスのvecAという名前の仮引数を入れています。
そしてFieldsがインスタンス化された時点で初期化するvalueとの足し算を行っています。
そしてmain.cppでクラス同士の演算を行っています。
main.cpp(主要部分のみ)
|
1 2 3 4 5 6 7 8 9 10 |
//演算子のオーバーロード Fields A_Fields; Fields B_Fields; Fields C_Fields; C_Fields = A_Fields + B_Fields; cout << "C_Fields.value = " << C_Fields.value << endl; C_Fields = A_Fields.operator+(B_Fields); cout << "C_Fields.value = " << C_Fields.value << endl; |
【結果】
|
1 2 |
C_Fields.value = 4 C_Fields.value = 4 |
「C_Fields = A_Fields + B_Fields;」がクラス同士の演算です。
実際は関数内でFieldsクラス内のメンバ変数valueの足し算を行っています。
これは、その下の「C_Fields = A_Fields.operator+(B_Fields);」と同じ処理を行っています。こちらの書き方の方がクラス内のメンバ関数に引数「B_Fields」を渡して計算しているのでプログラムとしては理解しやすいですが、上記の書き方の方がプログラミングの文法とは離れて直感的ですよね。
別の2つのクラス同士の演算も可能です。
Fields.h
|
1 2 |
//演算子のオーバーロード friend Fields operator+(const Fields&, const Fields&); |
クラス内のprivateやprotectedメンバ変数は、基本的に同じクラス内のメンバ関数からしかアクセスできませんが、フレンド機能を使うと通常の関数からもアクセスできるようになります。
Fields.cpp(主要部分のみ)
|
1 2 3 4 5 6 7 |
Fields operator+(const Fields& vecA, const Fields& vecB) { Fields temp; temp.value = vecA.value + vecB.value; return temp; } |
main.cpp(主要部分のみ)
|
1 2 3 4 5 6 7 |
//演算子のオーバーロード Fields A_Fields; Fields B_Fields; Fields C_Fields; C_Fields = A_Fields + B_Fields; cout << "C_Fields.value = " << C_Fields.value << endl; |
【結果】
|
1 |
C_Fields.value = 4 |
では、この機能を使ってクラス同士の演算子を自作します。
Fields.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
#ifndef FIELDS_H #define FIELDS_H #include "Mesh.h" #include <vector> using std::vector; class Fields { public: Fields();//constructor virtual ~Fields(); //deconstructor typedef vector<Fields> vectorField1d; double x1d; //x座標 double value; //Uの値 //vector<Fields> passGridinfomation(vector<Fields>&, Mesh&); Fields::vectorField1d passGridinfomation(Fields::vectorField1d&, vector<double>&); //add 演算子のオーバーロード friend Fields::vectorField1d operator+(const Fields::vectorField1d&, const Fields::vectorField1d&); friend Fields::vectorField1d operator-(const Fields::vectorField1d&, const Fields::vectorField1d&); friend Fields::vectorField1d operator&&(const Fields::vectorField1d&, const Fields::vectorField1d&); friend Fields::vectorField1d operator*(const double&, const Fields::vectorField1d&); friend Fields::vectorField1d operator*(const Fields::vectorField1d&, const double&); }; #endif //FIELDS_H |
Fields.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#include "Mesh.h" #include <iostream> Mesh::Mesh() { std::cout << "Mesh::Mesh() constructor" << std::endl; } Mesh::Mesh(int& n, double& txlengthx): NumberOfNode(n),//x分割数 lengthx(txlengthx),//x方向長さ xpts(NumberOfNode, 0.0)//vector(要素数, 値) { std::cout << "Mesh::Mesh" << std::endl; dx1d = lengthx / (NumberOfNode-1); discritized1dgrid(xpts); //add } //add void Mesh::discritized1dgrid(vector<double>& vec) { for (int i = 1; i < vec.size(); i++) //vec[0]=0なのでi=1からループする { vec[i] = vec[i - 1] + dx1d; } } //add end Mesh::~Mesh() { std::cout << "Mesh::~Mesh() deconstructor" << std::endl; } |
main.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include <iostream> #include <vector> #include "Mesh.h" #include "Fields.h"//add using namespace std; using std::vector; int main() { int Nx =10; double totallength = 2.0; Mesh mesh_(Nx, totallength);//Meshクラスのインスタンス化 /* cout << "mesh_.NumberOfNode = " << mesh_.NumberOfNode << endl; cout << "mesh_.lengthx = " << mesh_.lengthx << endl; cout << "mesh_.dx1d = " << mesh_.dx1d << endl; */ for (int i = 0; i < mesh_.xpts.size();i++) { cout << "xpts[" << i << "] = " << mesh_.xpts[i] << endl; } // UFields Fields FieldsOperations; cout << "UFieldsvec = " << FieldsOperations.value << endl; Fields::vectorField1d U(mesh_.NumberOfNode); // typedef vector<Fields> vectorField1d; U = FieldsOperations.passGridinfomation(U, mesh_.xpts); for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].x1d = " << U[i].x1d << endl; } for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].value = " << U[i].value << endl; } //add 演算子のオーバーロード double myvalue = 20.0; double myvalue1 = 10.0; Fields::vectorField1d tempResult = U + U; Fields::vectorField1d tempMultiResult = myvalue * U; Fields::vectorField1d tempMultiResult1 = U * myvalue1; for (int i = 0; i < U.size(); i++) { cout << "tempResult[" << i << "] = " << tempResult[i].value << endl; } for (int i = 0; i < U.size(); i++) { cout << "tempMultiResult[" << i << "] = " << tempMultiResult[i].value << endl; } for (int i = 0; i < U.size(); i++) { cout << "tempMultiResult1[" << i << "] = " << tempMultiResult1[i].value << endl; } return 0; } |
「tempResult[i].value」「tempMultiResult[i].value」「tempMultiResult1[i].value」の出力にfor文で3つも同じ記述をしているのは無駄が多いですが、後ほど関数にまとめるとして今はそのままにしておきます。
【結果】
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
Mesh::Mesh xpts[0] = 0 xpts[1] = 0.222222 xpts[2] = 0.444444 xpts[3] = 0.666667 xpts[4] = 0.888889 xpts[5] = 1.11111 xpts[6] = 1.33333 xpts[7] = 1.55556 xpts[8] = 1.77778 xpts[9] = 2 UFieldsvec = 2 Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor U[0].x1d = 0 U[1].x1d = 0.222222 U[2].x1d = 0.444444 U[3].x1d = 0.666667 U[4].x1d = 0.888889 U[5].x1d = 1.11111 U[6].x1d = 1.33333 U[7].x1d = 1.55556 U[8].x1d = 1.77778 U[9].x1d = 2 U[0].value = 2 U[1].value = 2 U[2].value = 2 U[3].value = 2 U[4].value = 2 U[5].value = 2 U[6].value = 2 U[7].value = 2 U[8].value = 2 U[9].value = 2 tempResult[0] = 4 tempResult[1] = 4 tempResult[2] = 4 tempResult[3] = 4 tempResult[4] = 4 tempResult[5] = 4 tempResult[6] = 4 tempResult[7] = 4 tempResult[8] = 4 tempResult[9] = 4 tempMultiResult[0] = 40 tempMultiResult[1] = 40 tempMultiResult[2] = 40 tempMultiResult[3] = 40 tempMultiResult[4] = 40 tempMultiResult[5] = 40 tempMultiResult[6] = 40 tempMultiResult[7] = 40 tempMultiResult[8] = 40 tempMultiResult[9] = 40 tempMultiResult1[0] = 20 tempMultiResult1[1] = 20 tempMultiResult1[2] = 20 tempMultiResult1[3] = 20 tempMultiResult1[4] = 20 tempMultiResult1[5] = 20 tempMultiResult1[6] = 20 tempMultiResult1[7] = 20 tempMultiResult1[8] = 20 tempMultiResult1[9] = 20 Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Fields::~Fields() destructor Mesh::~Mesh() deconstructor |
クラス同士の演算が可能になりました。
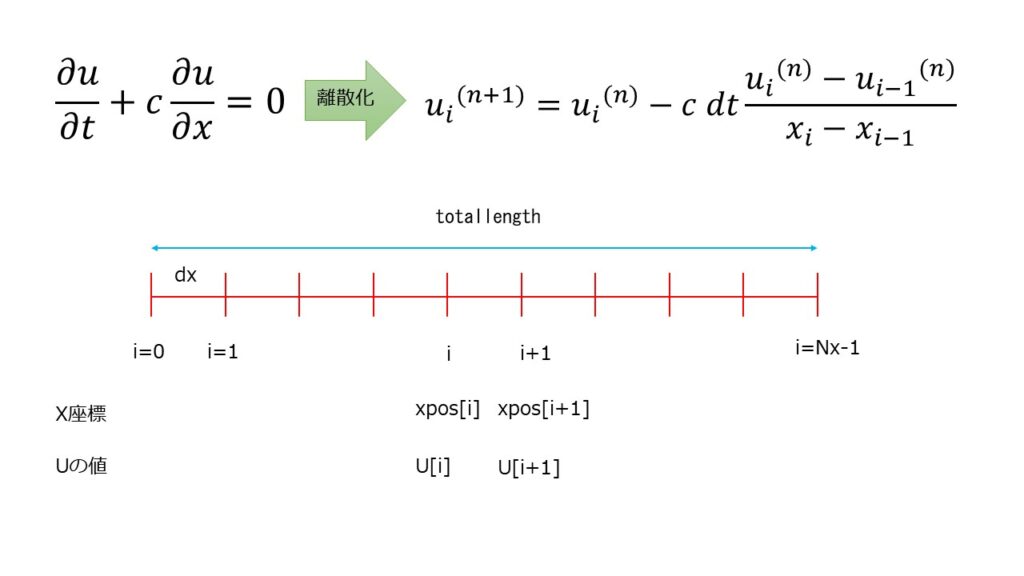
Step5:微分の離散化
1次元移流方程式について微分を離散化して扱います。
微分の離散化を定義するため以下の2つのファイルを作成します。
- Diff1d.h
- Diff1d.cpp
Diff1d.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#ifndef DIFF1D_H #define DIFF1D_H #include "Mesh.h" #include <vector> #include"Fields.h" using std::vector; namespace fd1d { // U U U U //*-----*----*----* // i-1 i class Diff1d { public: Diff1d(); Fields::vectorField1d gradX1d(Fields::vectorField1d&); virtual ~Diff1d(); }; } #endif //FIELDS_H |
今後のためクラス名が被らないように名前空間「fd1d」を付けてクラスを定義します。
返すデータの型はvectorField1dは「vector<Fields>」を意味することは説明済みです。これによりFieldsクラスを持ったvecotorコンテナの配列を引数に入れて「gradX1d」の関数処理を行い、Fieldsクラスを持ったvecotorコンテナの配列が返ってくるよう定義します。
Diff1d.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#include "Diff1d.h" #include <iostream> fd1d::Diff1d::Diff1d() { } Fields::vectorField1d fd1d::Diff1d::gradX1d(Fields::vectorField1d& vec) { Fields::vectorField1d temp = vec; for (int i = 1; i < vec.size()-1; i++) { temp[i].value = (vec[i].value - vec[i - 1].value) / (vec[i].x1d - vec[i - 1].x1d); } return temp; } fd1d::Diff1d::~Diff1d() { std::cout << "fd1d::Diff1D::~Diff1D() destructor" << std::endl; } |
こちらで関数の処理内容を書いています。
名前空間内のクラス内のメンバ関数の定義を行うには、先頭に「fd1d::」を付けて定義する必要があります。
以上で微分の離散化の関数処理が完成です。
以下で具体的に移流方程式を離散化した式を解くプログラムを書いていきます。
プログラムの中に「vec[i – 1].value」があるためi=0を代入するとエラーになります。
ですので、for (int i = 1; i < vec.size()-1; i++)として端はmain.cppで境界条件として設定するようにしています。