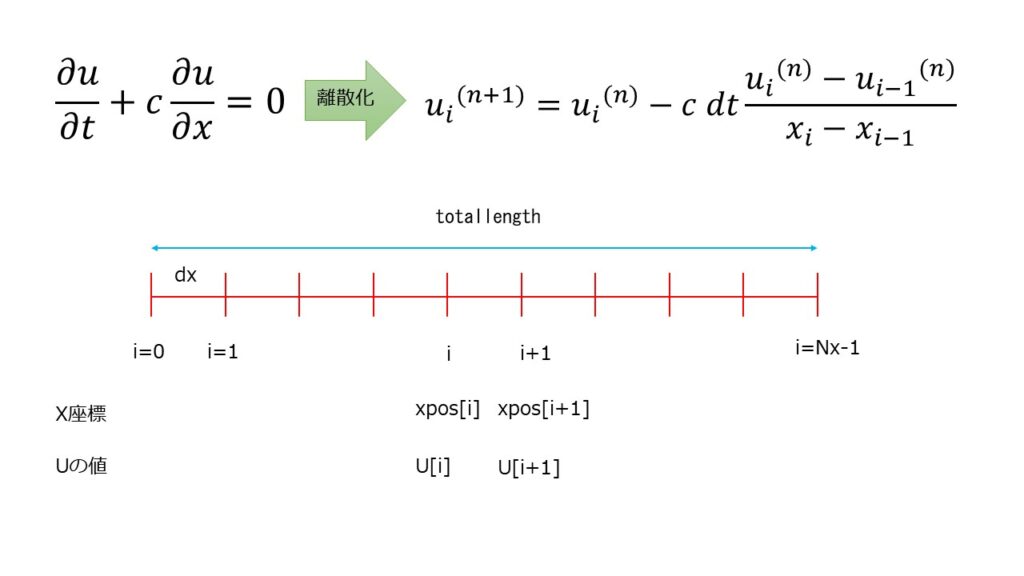
Step6:1次元移流方程式の離散化
以下の時間に対して$\frac{\partial }{\partial t}=\frac{u^{(n+1)_{i}}-u^{(n)_{i}}}{dt}$離散化を行うと、nステップ目の$u^{n}_{i}$に対してn+1ステップ目の$u^{n+1}_{i}$を求める式は以下のようになります。
- Solution1D.h
- Solution1D.cpp
Solution1D.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#ifndef SOLUTION_H #define SOLUTION_H class Solution1d { public: Solution1d(int&, double&); // constructor virtual ~Solution1d(); //deconstructor int nt; //ステップ数 double dt; //時間刻み幅 }; #endif |
以下の変数を定義しています。
- int nt; ステップ数
- double dt; 時間刻み幅
Solution1D.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#include <iostream> #include "Solution1D.h" Solution1d::Solution1d(int& nt_, double& dt_) : nt(nt_), dt(dt_) { std::cout << "Solution1d()" << std::endl; } Solution1d::~Solution1d() { std::cout << "~Solution1d()" << std::endl; } |
Solution1d::Solution1d(int& nt_, double& dt_)では初期化を行っているだけです。
main.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
#include <iostream> #include <vector> #include "Mesh.h" #include "Fields.h"//add #include "Diff1d.h"//add #include "Solution1D.h"//add using namespace std; using std::vector; int main() { int Nx =10; double totallength = 2.0; Mesh mesh_(Nx, totallength);//Meshクラスのインスタンス化 /* cout << "mesh_.NumberOfNode = " << mesh_.NumberOfNode << endl; cout << "mesh_.lengthx = " << mesh_.lengthx << endl; cout << "mesh_.dx1d = " << mesh_.dx1d << endl; */ for (int i = 0; i < mesh_.xpts.size();i++) { cout << "xpts[" << i << "] = " << mesh_.xpts[i] << endl; } // UFields Fields FieldsOperations; cout << "UFieldsvec = " << FieldsOperations.value << endl; Fields::vectorField1d U(mesh_.NumberOfNode); // typedef vector<Fields> vectorField1d; Fields::vectorField1d Unew(mesh_.NumberOfNode); U = FieldsOperations.passGridinfomation(U, mesh_.xpts); for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].x1d = " << U[i].x1d << endl; } for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].value = " << U[i].value << endl; } //initial condition cout << "Initial :: Iteration completed, writing the final file" << endl; for (int i = 0; i < U.size(); i++) { U[i].value = 1.0; if ((U[i].x1d > 0.5) && (U[i].x1d < 1.0)) { U[i].value = 2.0; } } // solution class int ntimestep = 500; double dt = 0.001; fd1d::Diff1d diff1d; Solution1d sol1d(ntimestep, dt); for (int nt = 0; nt < sol1d.nt; nt++) { cout << "Iteration no : " << nt << endl; U = Unew; double wavespeed = 1.0; double cdt = sol1d.dt * wavespeed; Fields::vectorField1d Diff = diff1d.gradX1d(U); Unew = U - (cdt * Diff); // du/dt = c*du/dx => Unew{i} = U{i} - c(u{i} - u{i-1})/dx // ノイマン条件 Unew[0].value = Unew[1].value; Unew[U.size() - 1].value = Unew[U.size() - 2].value; } return 0; } |
計算領域の端はノイマン条件(微分値が0)としています。
|
1 2 3 |
// ノイマン条件 Unew[0].value = Unew[1].value; Unew[U.size() - 1].value = Unew[U.size() - 2].value; |
これでプログラムの主要部分は完成です。
以下の部分でステップ数を増やして計算しています。
|
1 2 3 4 |
for (int nt = 0; nt < sol1d.nt; nt++) { (省略) } |
以下の部分で波動関数$u$の形の初期化を行っています。
|
1 2 3 4 5 6 7 8 9 10 11 |
//initial condition cout << "Initial :: Iteration completed, writing the final file" << endl; for (int i = 0; i < U.size(); i++) { U[i].value = 1.0; if ((U[i].x1d > 0.5) && (U[i].x1d < 1.0)) { U[i].value = 2.0; } } |
しかし、計算を実行させても結果を出力するプログラムを作成していません。
次に結果を出力する関数を作成します。
※【イメージ】
初期状態と最終状態をプロットすると以下のようになります。
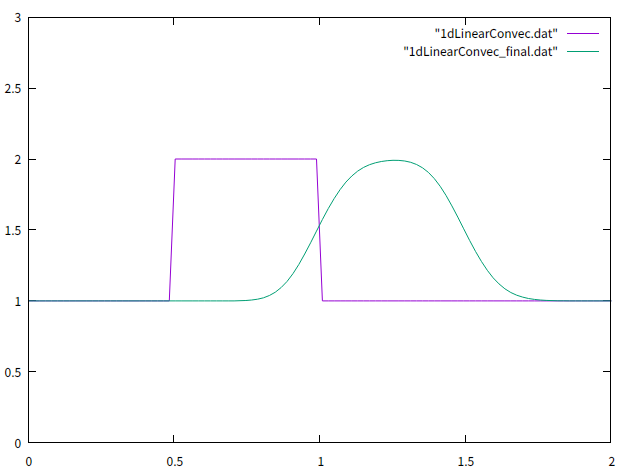
※移流方程式は理論上は形を変えずに伝播する方程式ですが離散化したことにより拡散が起こり波の形が変わっています。この修正は難しいので今を行わずプログラムの完成までに注力します。
Step7:ファイル出力
以下の2つのファイルを用意します。
- FileWriter.h
- FileWriter.cpp
FileWriter.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#ifndef FILEWRITWE_H #define FILEWRITWE_H #include <stdio.h> #include <iostream> #include <vector> #include <cmath> #include <string> #include <cstring> #include <sstream> #include <fstream> //ファイルの書き込みに必要 #include "Fields.h" using namespace std; using std::vector; using std::string; class FileWriter { public: FileWriter();//constructor virtual ~FileWriter(); //destructor void write1dField(Fields::vectorField1d&, string&); }; #endif |
FileWriter.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
#include "FileWriter.h" #include <iostream> FileWriter::FileWriter() { } void FileWriter::write1dField(Fields::vectorField1d& vec, string& name_) { string myfileType = ".dat"; //拡張子 string path = "C:\\work\\C_lang\\20220413_diff_C_puls\\\004_NS_Eq_1D_blog\\1DNS\\1DNS\\"; //絶対パス string pathName = path.append(name_).append(myfileType); //"myOutput;" + ".dat" => "myOutput.dat" std::cout << "pathName = " << pathName << " : pathName.size() = " << pathName.size() << std::endl; //char* cstr = new char[pathName.size() + 2]; // メモリ確保 //std::cout << "cstr = " << &cstr << std::endl; //strcpy_s(cstr, name2.size() + 2, name2.c_str()); FILE* outfile; fopen_s(&outfile, pathName.c_str(), "w+t"); //https://www.paveway.info/entry/2018/12/25/cpp_std_string_char std::cout << "outfile = " << &outfile << std::endl; for (int i = 0; i < vec.size(); i++) { double xpos = vec[i].x1d; double uvel = vec[i].value; if (outfile) { fprintf(outfile, "%5.8lf\t%5.8lf\n", xpos, uvel); cout << "Done Writing!" << endl; } } fclose(outfile); } FileWriter::~FileWriter() { std::cout << "~filewriter() destructor" << std::endl; } |
そしてmain.cppに初期状態と最終状態の波形の出力を行います。
main.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
#include <iostream> #include <vector> #include "Mesh.h" #include "Fields.h" #include "Diff1d.h" #include "Solution1D.h" #include "FileWriter.h" //add using namespace std; using std::vector; int main() { int Nx =100; double totallength = 2.0; Mesh mesh_(Nx, totallength);//Meshクラスのインスタンス化 /* cout << "mesh_.NumberOfNode = " << mesh_.NumberOfNode << endl; cout << "mesh_.lengthx = " << mesh_.lengthx << endl; cout << "mesh_.dx1d = " << mesh_.dx1d << endl; */ for (int i = 0; i < mesh_.xpts.size();i++) { cout << "xpts[" << i << "] = " << mesh_.xpts[i] << endl; } // UFields(typedef vector<Fields> vectorField1d;) Fields FieldsOperations; Fields::vectorField1d U(mesh_.NumberOfNode); // typedef vector<Fields> vectorField1d; Fields::vectorField1d Unew(mesh_.NumberOfNode); U = FieldsOperations.passGridinfomation(U, mesh_.xpts); Unew = FieldsOperations.passGridinfomation(Unew, mesh_.xpts); for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].x1d = " << U[i].x1d << endl; } for (int i = 0; i < U.size(); i++) { cout << "U[" << i << "].value = " << U[i].value << endl; } //initial condition cout << "Initial :: Iteration completed, writing the final file" << endl; for (int i = 0; i < U.size(); i++) { U[i].value = 1.0; if ((U[i].x1d > 0.5) && (U[i].x1d < 1.0)) { U[i].value = 2.0; } } Unew = U; //file writer string name = "1dLinearConvec"; FileWriter filewriterObject_; filewriterObject_.write1dField(U, name); // solution class int ntimestep = 500; double dt = 0.001; fd1d::Diff1d diff1d; Solution1d sol1d(ntimestep, dt); for (int nt = 0; nt < sol1d.nt; nt++) { cout << "Iteration no : " << nt << endl; U = Unew; double wavespeed = 1.0; double cdt = sol1d.dt * wavespeed; Fields::vectorField1d Diff = diff1d.gradX1d(U); Unew = U - (cdt * Diff); // du/dt = c*du/dx => Unew{i} = U{i} - c*dt(u{i} - u{i-1})/dx // ノイマン条件 Unew[0].value = Unew[1].value; Unew[U.size() - 1].value = Unew[U.size() - 2].value; } //file writer string name2 = "1dLinearConvec_final"; FileWriter filewriterObject_1; filewriterObject_1.write1dField(Unew, name2); return 0; } |
【結果】
同じフォルダ内に以下の2つのファイルが作成されていれば成功です。
- 1dLinearConvec.dat:初期状態
- 1dLinearConvec_final.dat:最終状態
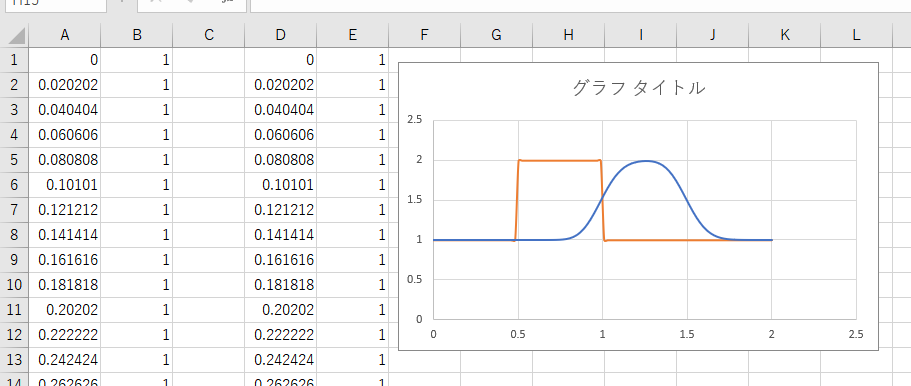
これらのデータを適当なソフトでグラフ化します。
今回は簡単にExcelで行うことにします。
- オレンジ:初期状態
- 薄青:最終状態(500ステップ目)
あとは余計なコメントや出力などを消して完成とします。