こんにちは(@t_kun_kamakiri)
前回の記事では移流方程式における移流項の離散化スキームを変えて結果がどう変わるかを検討しましたが、今回もその続きです。
前回の記事でも離散化スキームについて書きましたのでご参考ください。
今回は前回の記事以上に色々なスキームを試してみました。OpenFOAMに用意されているスキームは色々あるので自分で実装するよりも簡単にスキームの検討ができて便利ですよね。
勉強会などで「スキームなどを勉強したいけど、どうしたら良いのか」という質問もたまにあります。そんなときはナビエストークス方程式のような複雑な方程式ではなく、比較的簡単で理論解もある移流方程式で色々なスキームを試してみるのが良いでしょう。
本記事ではscalarTransportFoamは以下の偏微分方程式を解く非定常のソルバーを使います。
\frac{\partial T}{\partial t}+\nabla\cdot(\boldsymbol{u}T)-\nabla\cdot (D_{T}\nabla T)=\boldsymbol{S}_{T}\tag{1}
\end{align*}
流体の第二項の対流項$u\frac{\partial T}{\partial x}$の微分の離散化方法によっては、数値解が異なることがあります。異なると言っても、通常は流体のナビエストークスには流体粘性ので不連続解を分散させて解が振動しないようにしますし、不連続な解が出ることも稀なのでどのような離散化手法をとってもあまり解が変わりません。
ただ、衝撃波が出ると速度や圧力の不連続解が生じ、さらに粘性項より対流項が大きくなるので上記に近い方程式になります。
離散化スキームを以下のようにざっくり分けて特徴をまとめておきます。
upwind_difference.pdf (xrea.com)
- 1次精度:風上差分(upwind)→こちらは安定だが解が拡散してしまう
- 2次精度:中心差分、QUICK→こちらは不連続解をシャープにとらえようとするが、数値振動が起こりやすい
- TVDスキーム:minmod、vanLeer、vanAlbada、superBeeが有名。
色々な種類がありますが、不連続部分で振動を抑えるようにしながら、解はシャープにとらえようとするいい感じのスキーム
離散化スキームの種類はむちゃくちゃありますので、まずはこれくらいざっくりわけて特徴を理解しておくとよいでしょう。
- OpenFOAMでの移流項での離散化スキームについて結果比較
- Pythonで計算を自動化
※離散化の理論的な解説は割愛します。
本記事は前回の記事とは以下の点で異なります。
- スカラー輸送方程式(scalarTransportFoam)に計算時間を追加
- 前回の記事よりも多く色々なスキームを試した
- グラフに計算時間を載せるようにした
ひとつひとつ解説していきます。
OpenFOAM-v2012(WSL2)
Python3.8.10(jupyter lab)
モデルの入手
移流方程式のモデルは前回の記事で作成しましたのでそちらをご参考ください。
サンプルモデルも用意したのでご利用ください。
- 【OpenFOAM】移流方程式で離散化スキームの勉強をする
- 【OpenFOAM】移流方程式で色々な離散化スキームをPythonで自動実行して試してみた
- モデル入手[追記]※最終モデルをgithubにアップしました。
モデルを入手して本記事の内容に沿って編集していくと再現できるでしょう。
フォルダ構成
フォルダ構成は以下のようになっています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
├── main.py ├── orgCase │ ├── 0 │ │ ├── T │ │ └── U │ ├── Allrun │ ├── constant │ │ ├── polyMesh │ │ │ ├── boundary │ │ │ ├── faces │ │ │ ├── neighbour │ │ │ ├── owner │ │ │ └── points │ │ └── transportProperties │ ├── post.foam │ └── system │ ├── blockMeshDict │ ├── controlDict │ ├── fvSchemes │ ├── fvSolution │ ├── sampleDict │ └── setFieldsDict ├── resultDir └── schemeTest |
- orgCase:元のケースファイル
- schemeTest:スキームの一覧
- Allrun:計算実行スクリプト
- main.py:計算の自動実行スクリプト
スカラー輸送方程式(scalarTransportFoam)に計算時間を追加
scalarTransportFoamは以下の偏微分方程式を解く非定常のソルバーです。
\frac{\partial T}{\partial t}+\nabla\cdot(\boldsymbol{u}T)-\nabla\cdot (D_{T}\nabla T)=\boldsymbol{S}_{T}\tag{1}
\end{align*}
本記事では(1)を少し簡単にするために、
- 生成項を0:$\boldsymbol{S}_{T}=0$
- 拡散項を0:$D_{T}=0$
- 流速は一定:$\boldsymbol{u}=(0.1, 0, 0)$
と設定するようにします。
- $\Delta x = \frac{1}{100} = 0.01$[m]
- $\Delta t = 0.01$[s]
なのでクーラン数$C=\frac{u\Delta t}{\Delta x }=0.1$としています。
クーラン数1だとSuperBeeでエラー出たので少し小さめにしておきました。
初期状態は以下のようになっています。
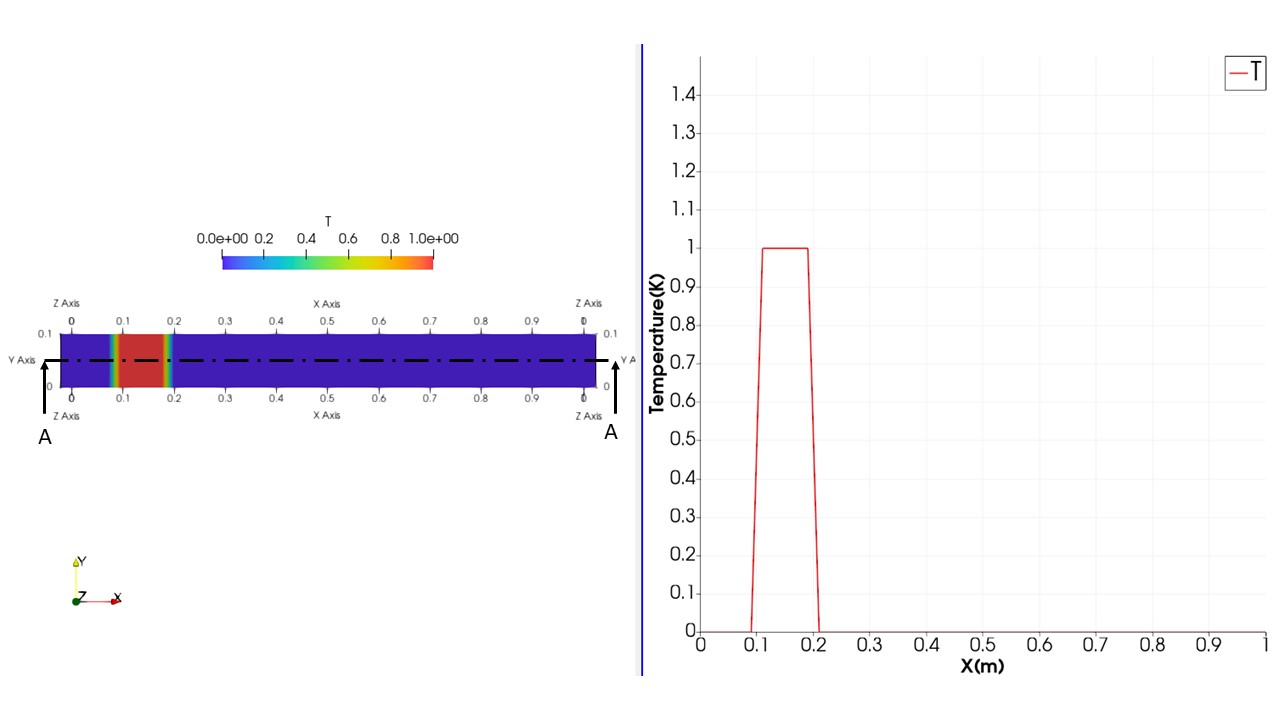
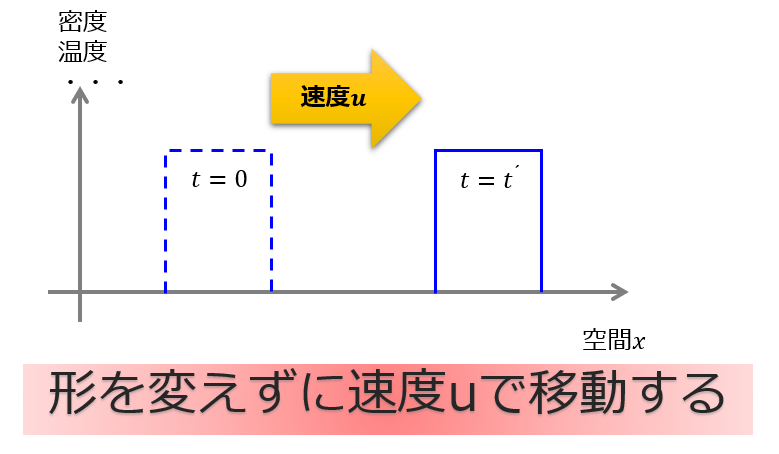
しかし、微分方程式を離散化して代数的に解くためどうしても近似的な解になってしまいます。どのような離散化スキームを使うとどういう結果になるのかを知ることが本記事の目的であります。
もう一つの目的は、離散化スキームによって計算時間が異なってくるため計算時間を調査することです。しかし、困ったことにscalarTransportFoamはデフォルトで計算時間を出力する関数が使われていないため、計算時間がわかりませんでした。
そこで計算時間を知るために以下の方法を考えました。
- system/controlDictにcodeを埋め込む
→上手くいかなかったので断念(自分がわかっていないだけなのでわかる方いたらコメント頂けると助かります_(._.)_)
追記:「time -f ‘,%U’ scalarTransportFoam > log.scalarTransportFoam」でコマンドを実行するのに使用したユーザーCPU時間が計測できるようです。
なので②のようにCPU計測のための関数を追加しなくても良かったです… - カスタマイズする
関数「runTime.printExecutionTime(Info); //Add」を追加するだけなのでこちらを採用します。
②の方法を採用しソルバにちょこっと関数を追加することで計算時間を出力するようにしました。
では、以下のコマンドでソルバをコピーします。
|
1 |
cp -r $FOAM_APP/solvers/basic/scalarTransportFoam MyscalarTransportFoam |
今回は使い捨てコードでローカルにコピーしても動作するコードなのでローカルにコピーして編集します。
フォルダ移動します。
|
1 |
cd MyscalarTransportFoam |
フォルダ構成は以下のようになっています。
|
1 2 3 4 5 6 |
. ├── Make │ ├── files │ └── options ├── scalarTransportFoam.C └── createFields.H |
ファイルの名前を変えます。
|
1 |
mv scalarTransportFoam.C MyscalarTransportFoam.C |
MyscalarTransportFoam.Cの時間のループの中に「runTime.printExecutionTime(Info); //Add」を追加して計算時間を出力するようにします。
MyscalarTransportFoam.C
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 |
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | \\ / A nd | www.openfoam.com \\/ M anipulation | ------------------------------------------------------------------------------- Copyright (C) 2011-2017 OpenFOAM Foundation ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application scalarTransportFoam Group grpBasicSolvers Description Passive scalar transport equation solver. \heading Solver details The equation is given by: \f[ \ddt{T} + \div \left(\vec{U} T\right) - \div \left(D_T \grad T \right) = S_{T} \f] Where: \vartable T | Passive scalar D_T | Diffusion coefficient S_T | Source \endvartable \heading Required fields \plaintable T | Passive scalar U | Velocity [m/s] \endplaintable \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "fvOptions.H" #include "simpleControl.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { argList::addNote ( "Passive scalar transport equation solver." ); #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" simpleControl simple(mesh); #include "createFields.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nCalculating scalar transport\n" << endl; #include "CourantNo.H" while (simple.loop()) { Info<< "Time = " << runTime.timeName() << nl << endl; while (simple.correctNonOrthogonal()) { fvScalarMatrix TEqn ( fvm::ddt(T) + fvm::div(phi, T) - fvm::laplacian(DT, T) == fvOptions(T) ); TEqn.relax(); fvOptions.constrain(TEqn); TEqn.solve(); fvOptions.correct(T); } runTime.write(); runTime.printExecutionTime(Info); //Add } Info<< "End\n" << endl; return 0; } // ************************************************************************* // |
そして実行ファイルを出力する先を指定してコマンドに名前を付けます。
Make/files
|
1 2 3 |
MyscalarTransportFoam.C EXE = $(FOAM_USER_APPBIN)/MyscalarTransportFoam |
以下のコマンドコンパイルします。
|
1 |
wmake |
これで「\$FOAM_USER_APPBIN」にMyscalarTransportFoamという実行ファイルが生成されています。ちなみに環境変数は「\$FOAM_USER_APPBIN=/home/ユーザ名/OpenFOAM/kamakiri-v2012/platforms/linux64Gcc63DPInt32Opt/bin」となっています。
では、計算時間を出力してくれるかを確認しましょう。
フォルダを移動して、
|
1 |
cd ../orgCase |
以下のコマンドで計算を実行します。
|
1 |
MyscalarTransportFoam |
計算のログに「ExecutionTime = 0.05 s 」などが出ていればオッケーです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Time = 0.01 DILUPBiCGStab: Solving for T, Initial residual = 0.00552486, Final residual = 6.37066e-19, No Iterations 1 ExecutionTime = 0.05 s ClockTime = 0 s Time = 0.02 DILUPBiCGStab: Solving for T, Initial residual = 0.00558659, Final residual = 7.33487e-19, No Iterations 1 ExecutionTime = 0.05 s ClockTime = 0 s Time = 0.03 DILUPBiCGStab: Solving for T, Initial residual = 0.00562634, Final residual = 1.54832e-18, No Iterations 1 ExecutionTime = 0.05 s ClockTime = 0 s (以下省略) |
計算時間の桁数はもう少し多くほしいですが・・・・
scalarTransportFoamの処理時間を知りたかったけど記述がなかったから、
runTime.printExecutionTime(Info);
を追加してみたけどコードを追っていくと結局<ctime>を使っていて10[ms]程度の分解能しかないというところまで理解した_(._.)_ https://t.co/Hb7mWab7WF— カマキリ🐲技術士勉強中 (@t_kun_kamakiri) February 19, 2023
複数回計算させて平均を取るかもう少し大きなモデルで解析をするかなど考えないといけませんね。
ひとまず正常に動作しているようであれば、初期状態に戻しておきましょう。
以下のコマンドでメッシュ状態はそのままで計算した結果だけを削除することができます。
|
1 |
foamListTimes -rm |
では、Pythonコードのあるフォルダに戻ります。
|
1 |
cd .. |
前回の記事よりも多く色々なスキームを試した
schemeTestというファイルにスキームの一覧を記載します。
前回の記事よりスキームは多くなっています。
schemeTest
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
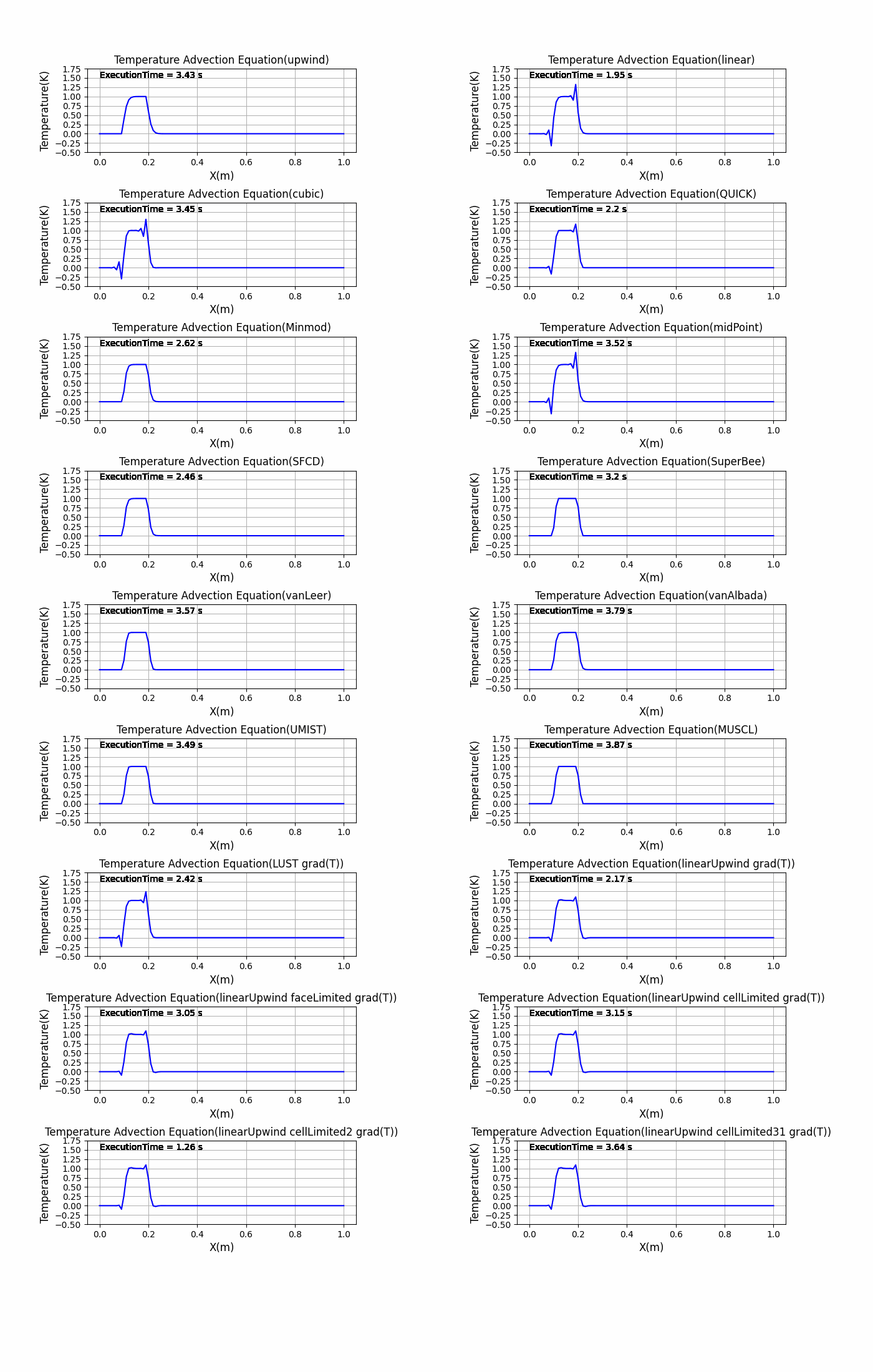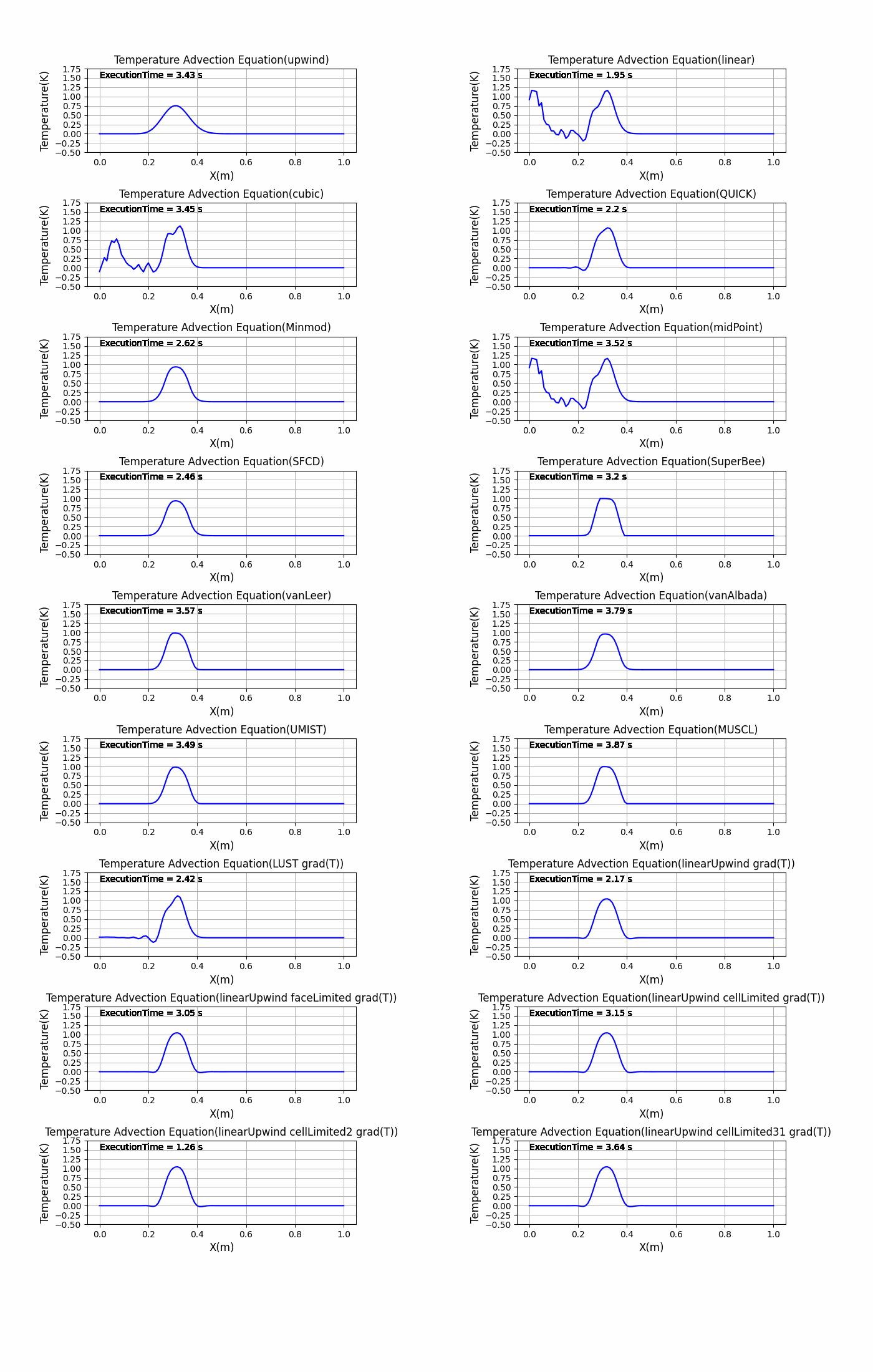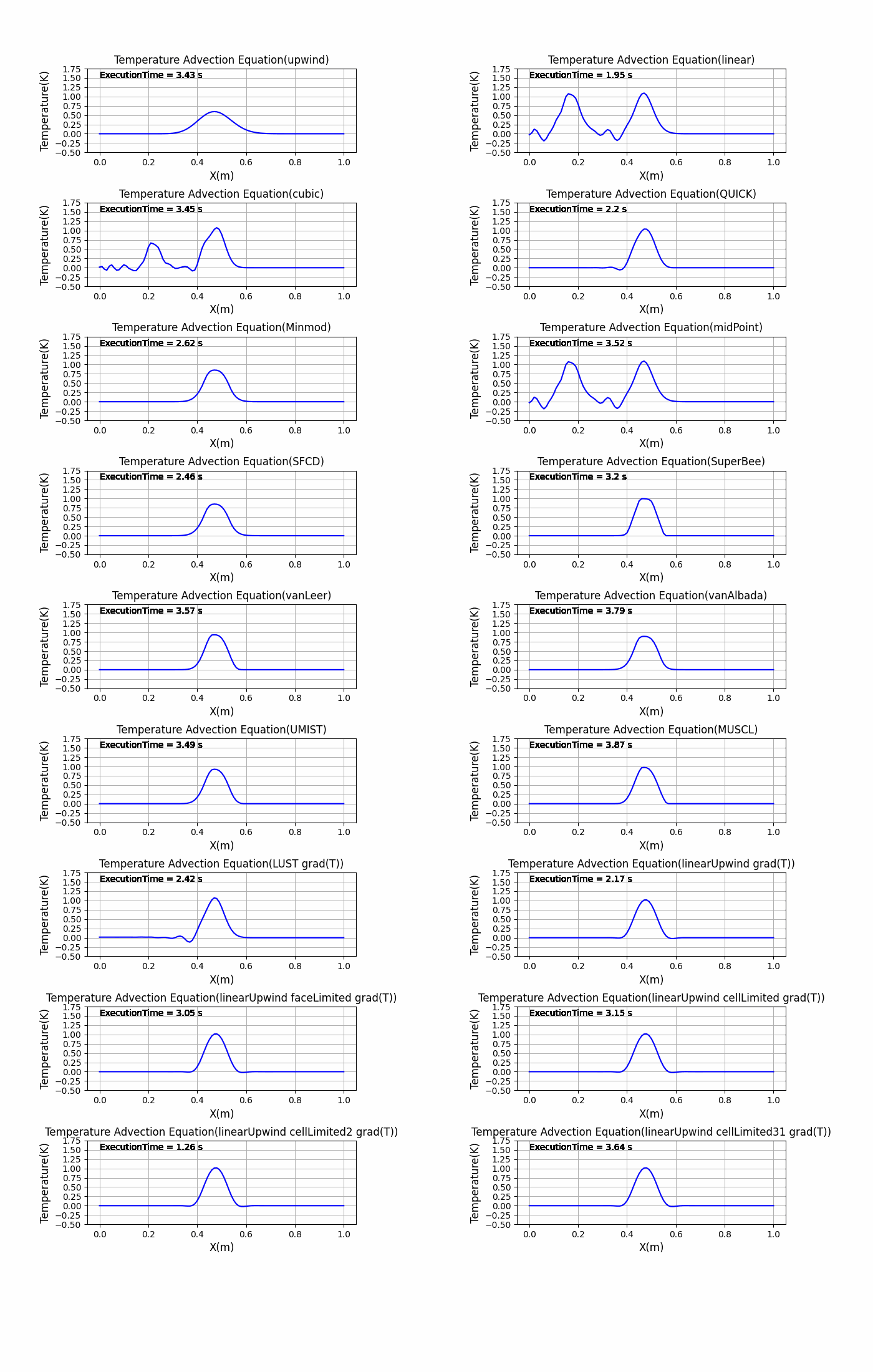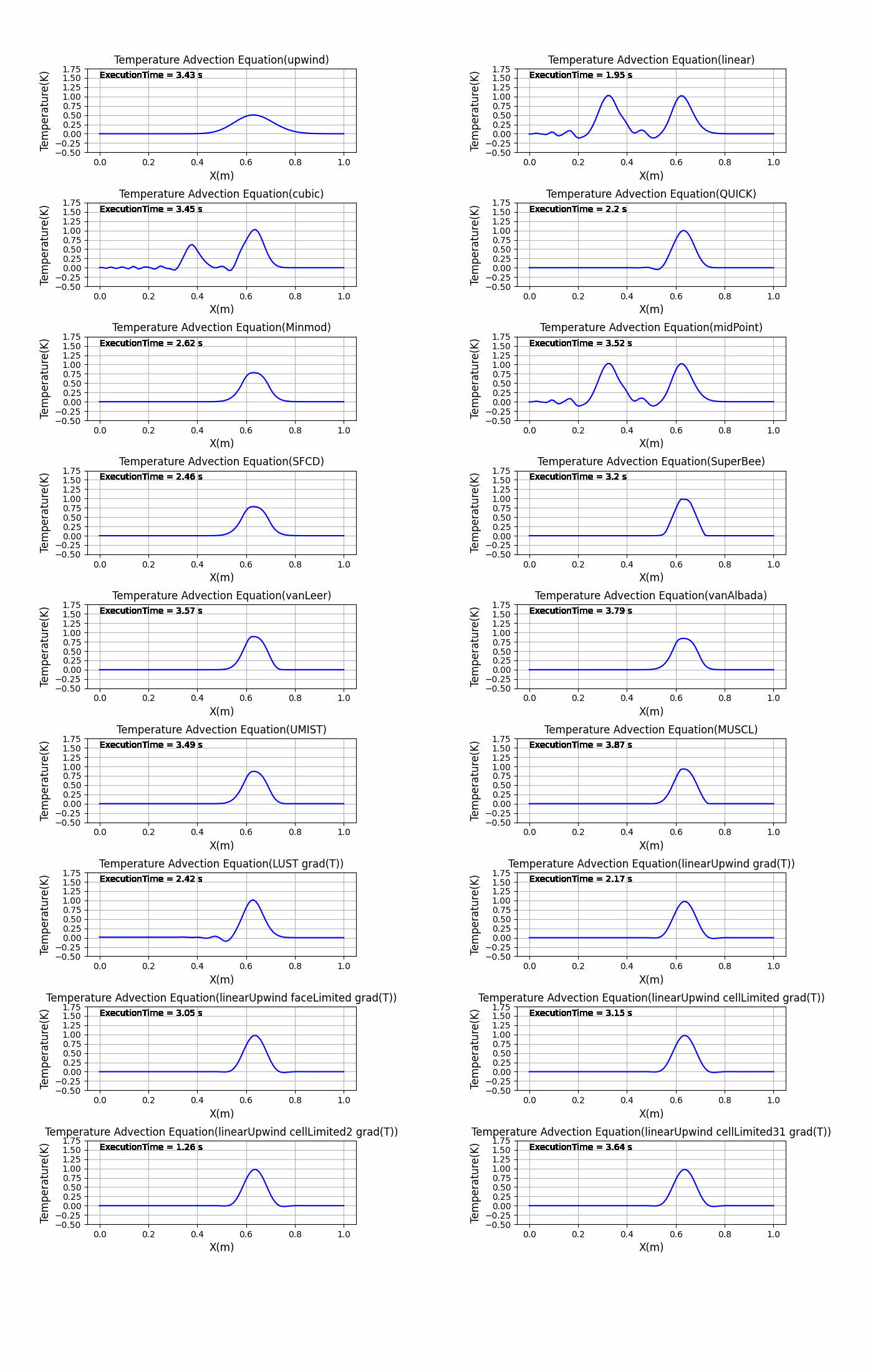
upwind linear cubic QUICK Minmod midPoint SFCD SuperBee vanLeer vanAlbada UMIST MUSCL LUST grad(T) linearUpwind grad(T) linearUpwind faceLimited grad(T) linearUpwind cellLimited grad(T) linearUpwind cellLimited2 grad(T) linearUpwind cellLimited31 grad(T) linearUpwind cellLimited32 grad(T) linearUpwind cellLimited33 grad(T) quadraticUpwindFit 1 cubicUpwindFit 1 limitedLinear 1 limitedCubic 1 limitedLinear 0.2 limitedLinear 0.5 limitedLinear 1.0 limitedCubic 0.2 limitedCubic 0.5 limitedCubic 1.0 Gamma 0.2 Gamma 0.5 Gamma 1.0 limitWith QUICK Minmod limitWith QUICK SuperBee limitWith QUICK vanAlbada |
グラフに計算時間を載せるようにした
今回は計算時間も測定してグラフに載せるようにしました。
計算時間はあくまで1回の計算をさせた場合での結果です。他のアプリの使用状態によってはCPUの使用状態も変わってくるので、本来は複数回計算させた際の平均値を取るのが良いでしょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
from pathlib import Path import shutil import subprocess import numpy as np from PyFoam.RunDictionary.ParsedParameterFile import ParsedParameterFile import matplotlib.pyplot as plt import os # スキームファイルを読み込む def open_SchemeList(): with open('./schemeTest') as f: scheme_list = [s.strip() for s in f.readlines()] return scheme_list # baseをコピーする def clone_file(orgCase, resultDir): "orgCaseをresultDirに重複しないようにコピー" baseName = Path(orgCase).name addName = None if addName!=None: baseName += f'_{addName}' Path(resultDir).mkdir(exist_ok=True, parents=True) n=0 newCase = Path(resultDir) / f'{baseName}_{n}' while newCase.is_dir(): n += 1 newCase = Path(resultDir) / f'{baseName}_{n}' shutil.copytree(orgCase, newCase) return newCase # スキームを入れ替える def new_parameter(newScheme, newCase): fileScheme = ParsedParameterFile(newCase / 'system/fvSchemes') fileScheme.content['divSchemes'] fileScheme.content['divSchemes']['div(phi,T)'] = f'Gauss {newScheme}' fileScheme.writeFile() # Allrunスクリプトを実行する(postProcess) def Allrun(newCase): "Allrunを実行" out_run = subprocess.check_output(['./Allrun'], cwd=newCase) return out_run.decode() # 計算時間の出力 def ExecutionTime_func(newCase, resultDir): print(f'Create figure {Path(newCase)/"log.MyscalarTransportFoam"}') with open( Path(newCase)/'log.MyscalarTransportFoam') as f: log_list = [s.strip() for s in f.readlines() if ('ExecutionTime' in s) or ('End' in s)] ExecutionTime = log_list[-2:][0].split('s')[0] + 's' print(ExecutionTime) if log_list[-1] != 'End': print("計算途中ストップ") return ExecutionTime # グラフにする def graph(scheme, ExecutionTime, newCase, resultDir): time_list = os.listdir(Path(newCase) / f'postProcessing/samples') plt.figure() for time in time_list[::7]: temp_data = np.loadtxt(Path(newCase) / f'postProcessing/samples/{time}/x_T_T.xy').T plt.plot(temp_data[0], temp_data[1],label=f'time = {time}') plt.grid() plt.yticks(np.arange(-0.5,2,0.25)) plt.legend() plt.xlabel("X(m)", fontsize=12) plt.ylabel("Temperature(K)", fontsize=12) plt.text(0, 2,ExecutionTime) plt.title(f"Temperature Advection Equation({scheme})", fontsize=14) # 画像賦存用データのフォルダ作成 result_graph_dir = Path(resultDir)/'savefig' if(os.path.isdir(result_graph_dir) == False): os.mkdir(result_graph_dir) # グラフを保存 plt.savefig(f'{result_graph_dir}/{scheme}.png') plt.close() # 全部のグラフを2列ずつにしてまとめる def Allgraph_png(scheme_list, ExecutionTime_list): fig = plt.figure(figsize = (14, 50)) for i, scheme in enumerate(scheme_list): #グラフを表示する領域を,figオブジェクトとして作成. col = len(scheme_list)//2 + 1 ax1 = fig.add_subplot(col,2,i+1) time_list = os.listdir(f'./resultDir/orgCase_{i}/postProcessing/samples') for time in time_list[::7]: temp_data = np.loadtxt(f'./resultDir/orgCase_{i}/postProcessing/samples/{time}/x_T_T.xy').T ax1.plot(temp_data[0], temp_data[1],label=f'time = {time}') # 計算時間 ExecutionTime = ExecutionTime_list[i] plt.subplots_adjust(left=0.1, right=0.9, bottom=0.01, top=0.95, wspace=0.6, hspace=0.6) ax1.text(0, 1.5,ExecutionTime) ax1.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=8) ax1.grid() ax1.set_yticks(np.arange(-0.5,2,0.25)) ax1.set_xlabel("X(m)", fontsize=12) ax1.set_ylabel("Temperature(K)", fontsize=12) ax1.set_title(f"Temperature Advection Equation({scheme})", fontsize=12) # グラフを保存 fig.savefig('./graph_Allschemes.png') plt.close() #================== main ======================== orgCase = 'orgCase' resultDir = 'resultDir' # スキームのリスト scheme_list = open_SchemeList() print(f'スキームの数 : {len(scheme_list)}') ExecutionTime_list = [] # 計算実行 for i, scheme in enumerate(scheme_list): print(f'{i+1} ======== {scheme} =========') newCase = clone_file(orgCase, resultDir) # 関数を実行する new_parameter(scheme, newCase) # スキームを入れ替える Allrun(newCase) # 計算を実行 ExecutionTime = ExecutionTime_func(newCase, resultDir) # 計算時間を取得 ExecutionTime_list.append(ExecutionTime) graph(scheme, ExecutionTime, newCase, resultDir) # グラフ化 # 全てのグラフをまとめる Allgraph_png(scheme_list, ExecutionTime_list) |
Pythonを実行します。
Pythonで「system/fvSchemes」の「divSchemes」スキームを変えています。
|
1 2 3 4 5 |
divSchemes { default none; div(phi,T) Gauss upwind grad(T); } |
結果はスキームごとに分けて「resultDir/savefig」に画像を作成し保存、全てのスキームでの結果を「graph_AllShemes.png」に画像を作成し保存しています。
pythonを実行します。
|
1 |
python3 main.py |
以下のように計算が進みます。
|
1 2 3 4 5 6 7 8 |
スキームの数 : 36 1 ======== linear ========= Create figure resultDir/orgCase_36/log.MyscalarTransportFoam ExecutionTime = 3.43s 2 ======== cubic ========= Create figure resultDir/orgCase_37/log.MyscalarTransportFoam ExecutionTime = 1.95 s (以下省略) |
結果を確認
結果は「resultDir/savefig」に画像として保存するようにしていますのでじっくり眺めることができます。
全体のグラフの比較は「graph_Allschemes.png」で行うことができます。
graph_Allschemes.png
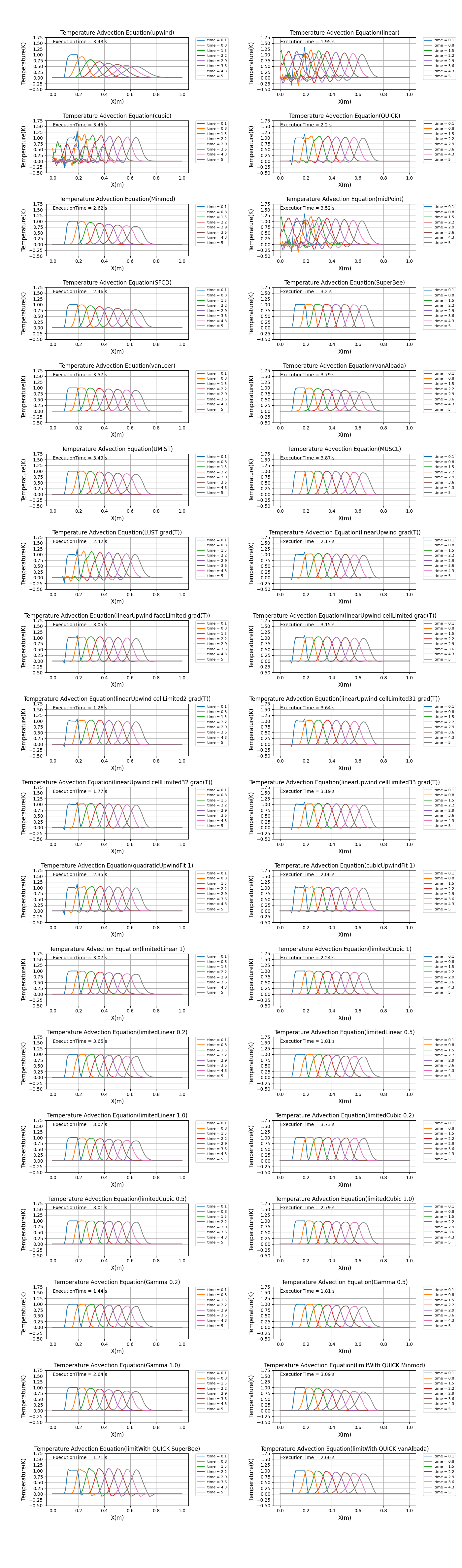
アニメーション作成
アニメーションにした方がわかりやすいかと思ったのでアニメーションにしてみました。
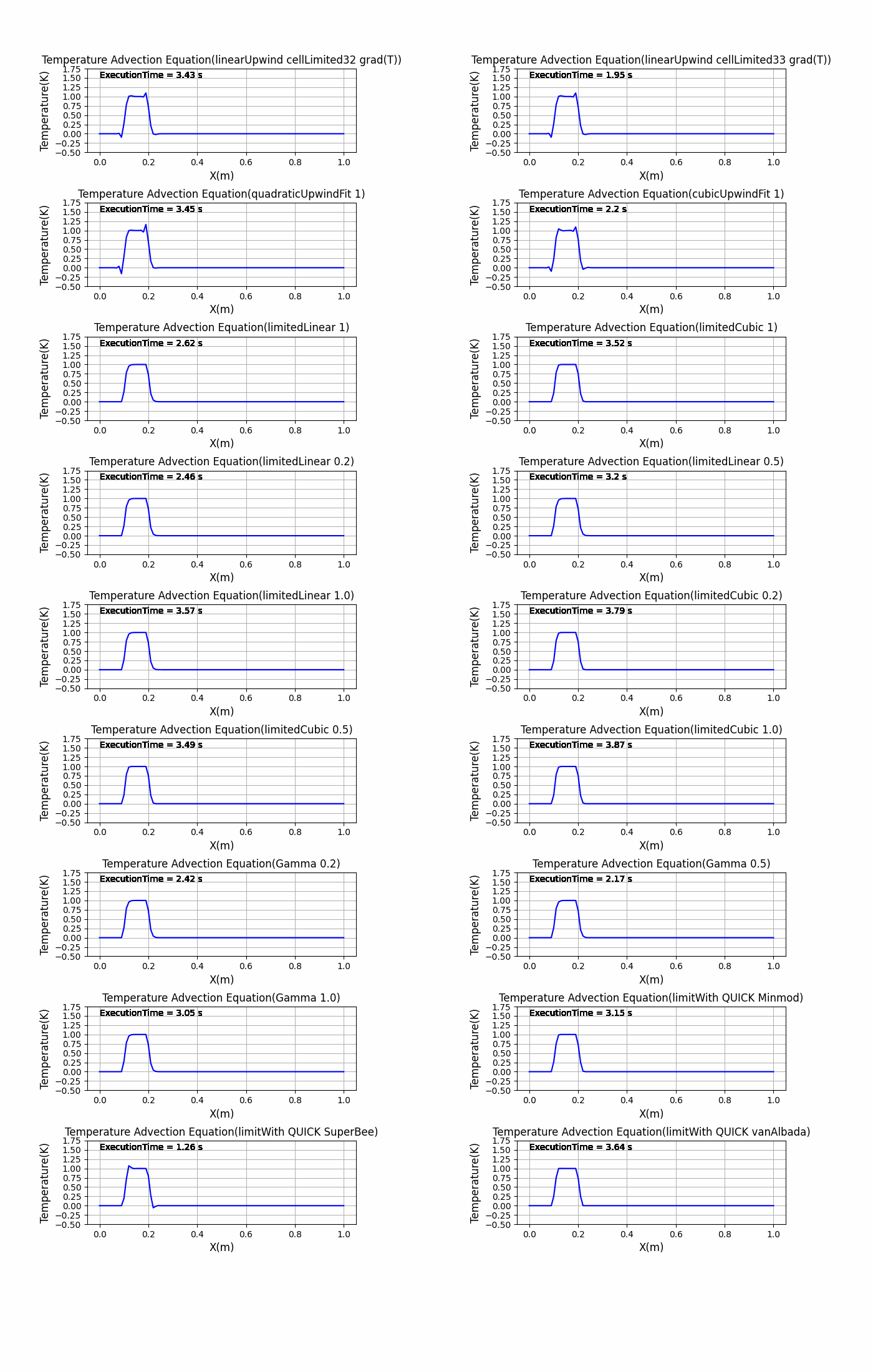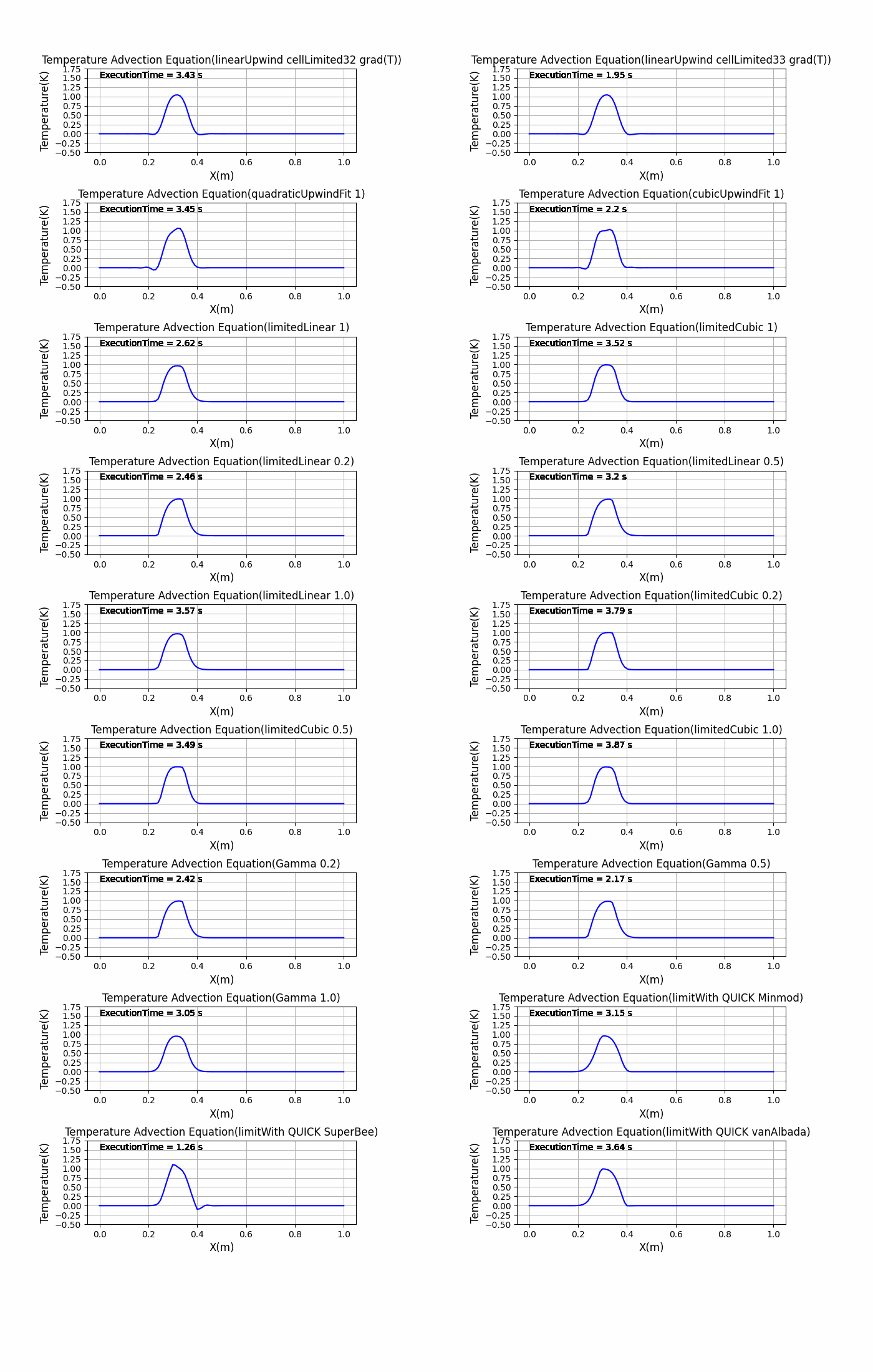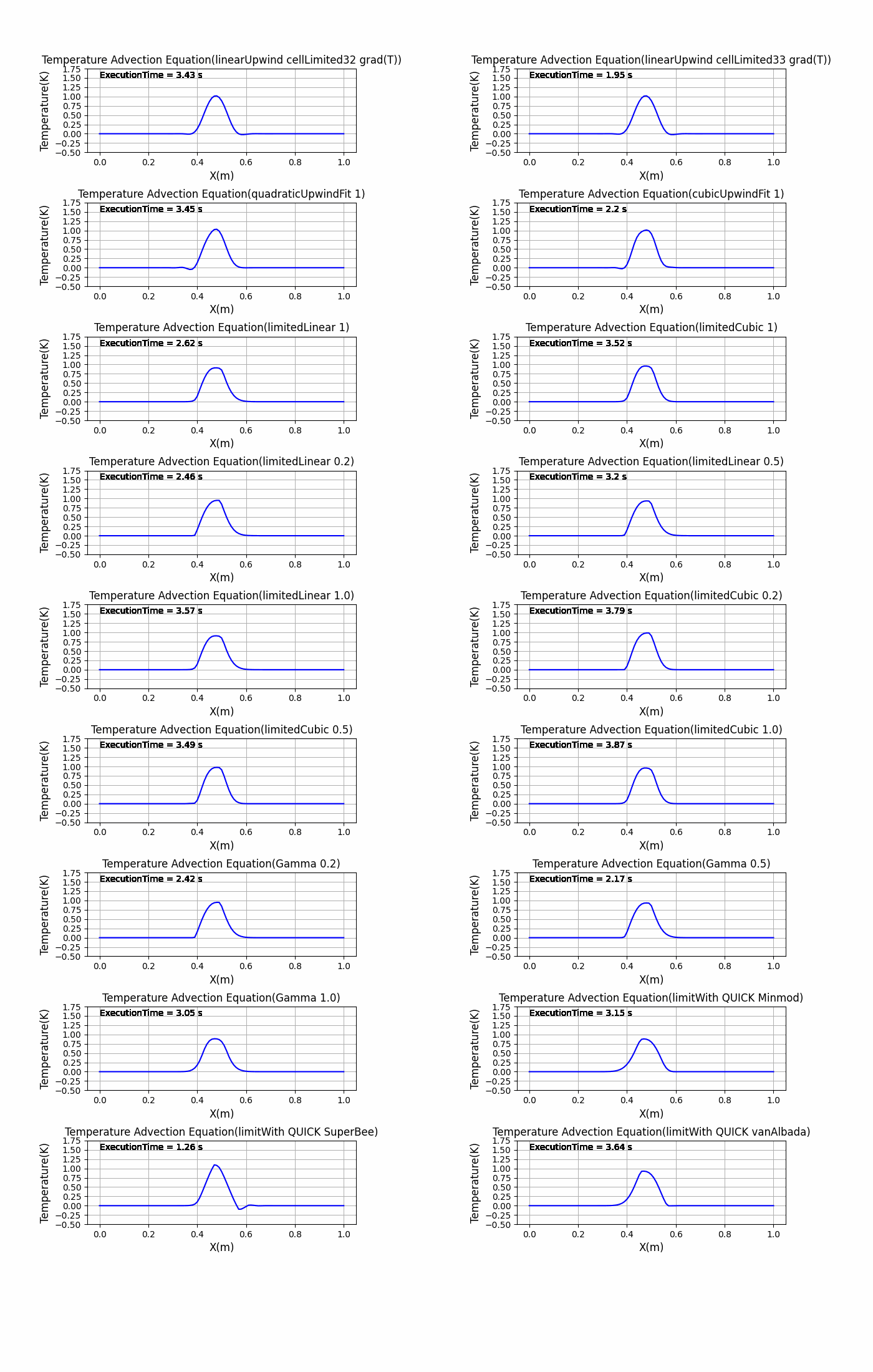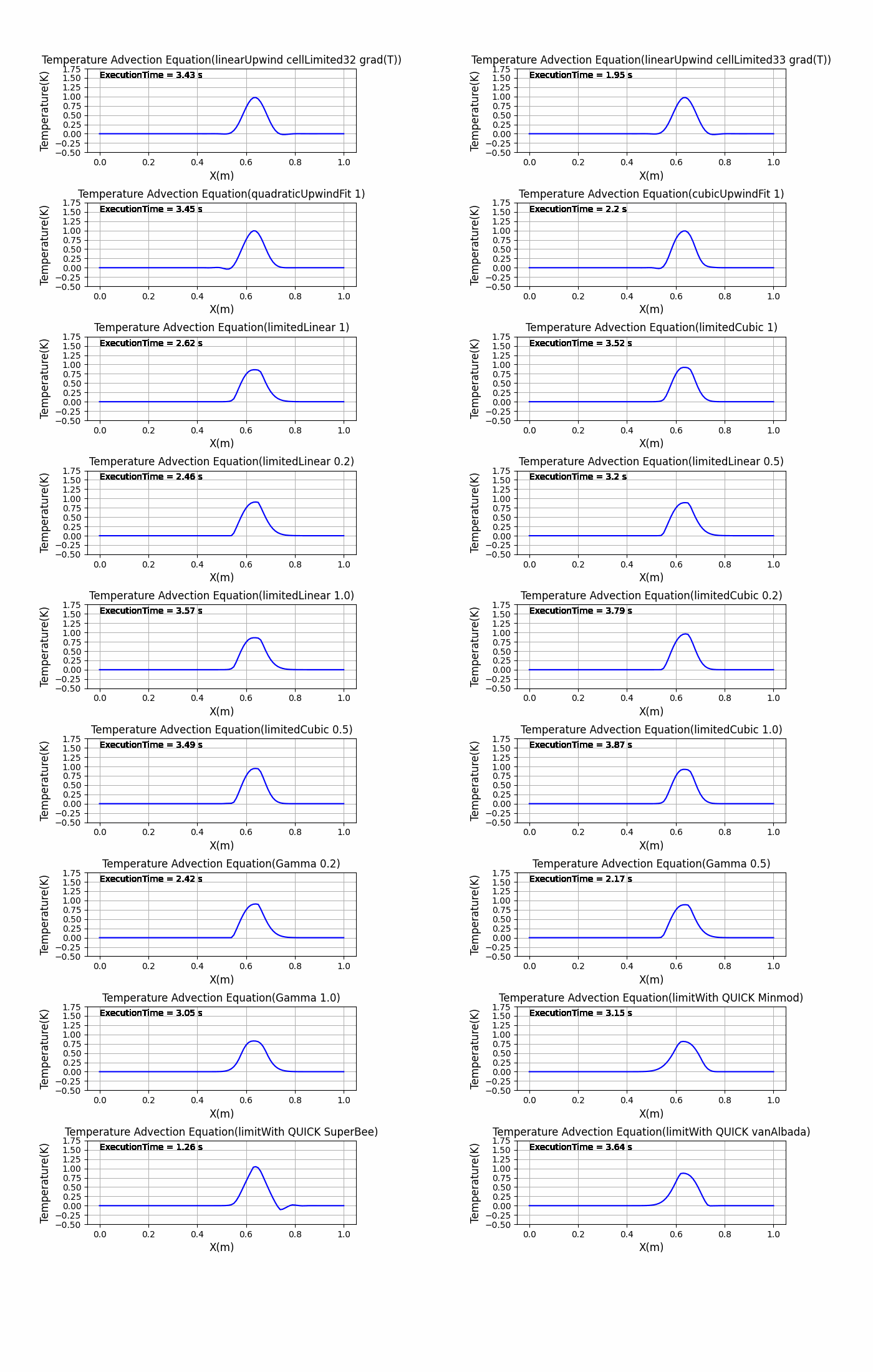
特に初期状態の矩形波の変化が激しい部分の微分を離散化が難しく、離散化スキームをどれにするかによって結果が変わるということがわかりました。これがもしsin波のような滑らかな初期状態だったり、拡散項があるとあまり結果に違いがでないかもしれません….(試す必要がありますね)
アニメーション作成用のコードは即興で作ったのでお粗末ですがご参考に…
先ほどのPythonコードに以下の関数を追加して実行すればOK。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
from matplotlib.animation import ArtistAnimation # 全部のグラフを2列ずつにしてまとめる def AllAnimation(scheme_list, ExecutionTime_list): ax_list = [] fig = plt.figure(figsize = (14, 50)) plt.subplots_adjust(left=0.1, right=0.9, bottom=0.01, top=0.95, wspace=0.6, hspace=0.6) time_list = os.listdir(f'./resultDir/orgCase_{0}/postProcessing/samples') for i, scheme in enumerate(scheme_list): #グラフを表示する領域を,figオブジェクトとして作成. col = len(scheme_list)//2 + 1 ax_list.append(fig.add_subplot(col,2,i+1)) frames = [] for time in time_list[::2]: frame = [] print(time) title = ax.text(0, 1.05, 'Time: {time}', fontsize=15) # 追加 for i, scheme in enumerate(scheme_list): temp_data = np.loadtxt(f'./resultDir/orgCase_{i}/postProcessing/samples/{time}/x_T_T.xy').T frame.append(ax_list[i].plot(temp_data[0], temp_data[1], color="blue")[0]) # 計算時間 ExecutionTime = ExecutionTime_list[i] ax_list[i].text(0, 1.5,ExecutionTime) ax_list[i].grid() ax_list[i].set_yticks(np.arange(-0.5,2,0.25)) ax_list[i].set_xlabel("X(m)", fontsize=12) ax_list[i].set_ylabel("Temperature(K)", fontsize=12) ax_list[i].set_title(f"Temperature Advection Equation({scheme})", fontsize=12) frames.append(frame) ani = ArtistAnimation(fig, frames, interval=1) ani.save("anim1-18.gif", writer="pillow") # ========== main ========== AllAnimation(scheme_list, ExecutionTime_list) |
まとめ
スキームは試して結果を眺めてみないとわからないので、本記事のような簡単な移流方程式で色々と試してみました。
今回は結果と計算時間だけを一覧で眺めれるようにしました。スキームによっては解が安定しなかったり、安定していても拡散する傾向にあったりします。離散化スキームの理論的な話は割愛しましたが、勉強するとなぜそのようなことが起こるのかがわかってきて理解が深まります。
- 対流項の発散スキームの比較
こちらはOpenFOAMの離散化スキームの比較として一番参考になる記事でしょう。 - Divergence scheme example
公式サイトにも離散化スキームに対する検討がされています。メッシュと離散化スキームの選択次第で結果がずいぶんと変わるのがわかるでしょう。 - OpenFOAM6.2 Numerical schemes
- OpenFOAM Basic Training
- 第1回オープンCAE講習会 OpenFOAM初中級講習B
- upwind_difference.pdf (xrea.com)
こちらのpdfはスキームについてよくまとめられています。
参考書
有限体積法の勉強にはこの本で間違いないです。
対流項目が中心差分で安定しないことを理論的に評価しておりとても参考になります。
有限体積法の詳しい解説として英語ですが以下の書籍を挙げておきます。
OpenFOAMに沿った解説もされているのでOpenFOAMを勉強する人にとっては有用です。
OpenFOAMの基本的な設定を学ぶことができる書籍として以下の参考書がお勧めです。
本書はESI版ではなくFoundation版でありOpenFOAMv2.xで書かれたやや古い内容です。その点に注意してESI版のお使いのversionとの違いを丁寧に調べることができる方であれば、十分参考になる書籍です。
OpenFOAM全般の設定などまとめられた書籍として以下のものがあります。
こちらもFoundation版なので、ESI版のお使いのversionとの違いを丁寧に調べることができる方であれば、十分参考になる書籍です。
こちらのオープンCAE学会から技術書典にOpenFOAMでメッシュ作成【PDF版】が出ています。難しい内容ではありますが、OpenFOAMのメッシュに関する内容が1000円で学べます。


![数値流体力学 [第2版]](https://m.media-amazon.com/images/I/51m13QQg5cL._SL500_.jpg)