こんにちは（@t_kun_kamakiri）
乱流モデルと壁関数の選択が解析結果に大きな影響を与えることをご存知でしょうか？
本記事では、乱流モデルと壁関数の違いを理解し、それをシミュレーションで確かめるためのモデルを構築する手順をご紹介します。
オープンソース流体解析ツールとしてはOpenFOAM利用し、初心者の方でもわかりやすいように、基本から丁寧に解説していきます。この記事を通じて、乱流解析における選択の重要性を深く理解し、実践的なスキルを身につけていきましょう。
前回の記事では平板流れの解析モデル作成と壁関数を用いた$y^+=100$程度での流速の速度分布について解説をしました。
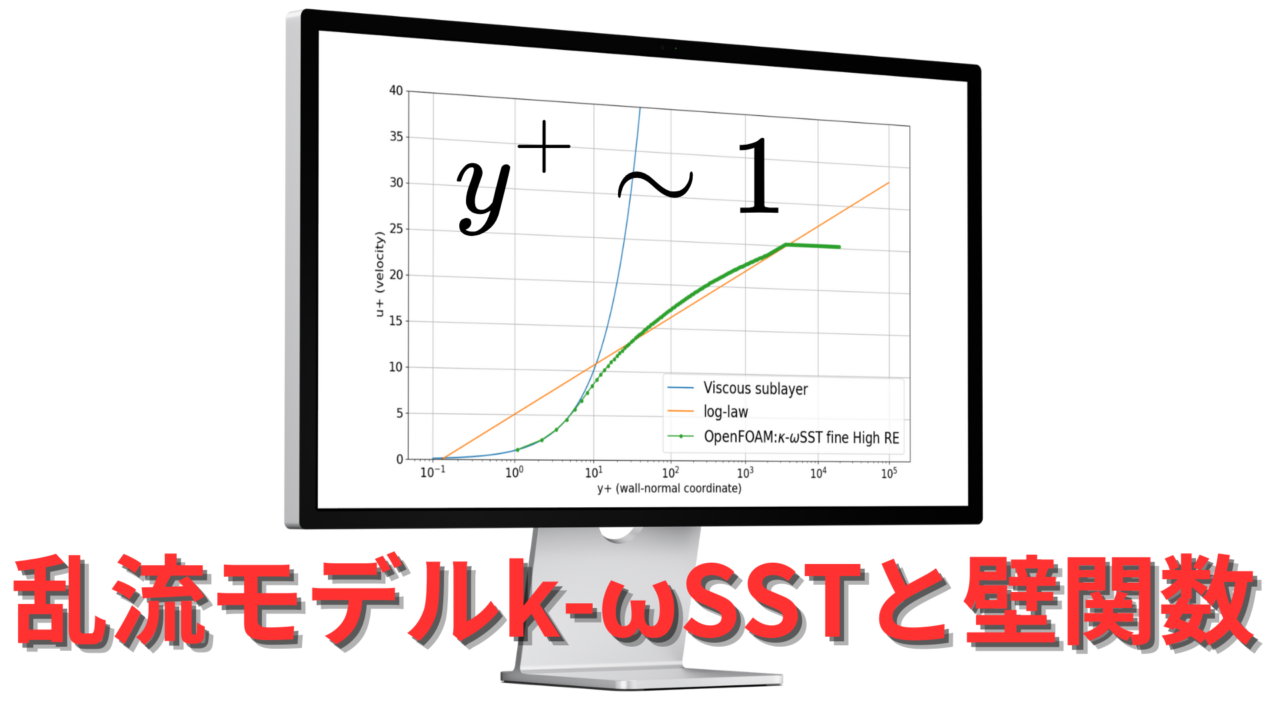
特に今回の記事では、乱流による渦動粘性が小さくなる粘性底層内までメッシュが作成されている場合（$y^+\sim 1$）での流速の速度分布について解説したいと思います。
- $y^+\sim 1$での平板流れの解析
- 速度分布の検証
WSLのUbuntu 22.04.05 LTS（OpenFOAM2412)
Python 3.11.9
$y^{+}\sim 1$となる状況
特にRANSなどの乱流モデルを使用する場合、$y^{+}=30\sim 300$程度にする必要があるというのを聞いたことがあるかもしれません。
それは高レイノルズ型の乱流モデルである$k$-$\varepsilon$モデルについての制約になります。
高レイノルズ型$k$-$\varepsilon$では、十分発達した乱流を想定して構築された数理モデルであるため、境界条件として壁関数を使う際は壁近傍の格子サイズは細かくしすぎず第一層の格子点は対数領域になるように厚く設定をします。
無次元化した$y^+$の第一格子点が対数則になっていると、壁面近傍で格子サイズを大きめに設定できるため格子数削減になります。また、乱流状態での分子粘性よりレイノルズ応力が大きく高レイノルズ数の乱流状態の速度分布になっています。
標準$k$-$\varepsilon$などの高レイノルズ型の乱流モデルを使う場合は、壁面極近傍の低レイノルズや壁面での乱れの非等方性を前提としてないため、第一格子点がどの位置に来ているかは非常に重要になります。
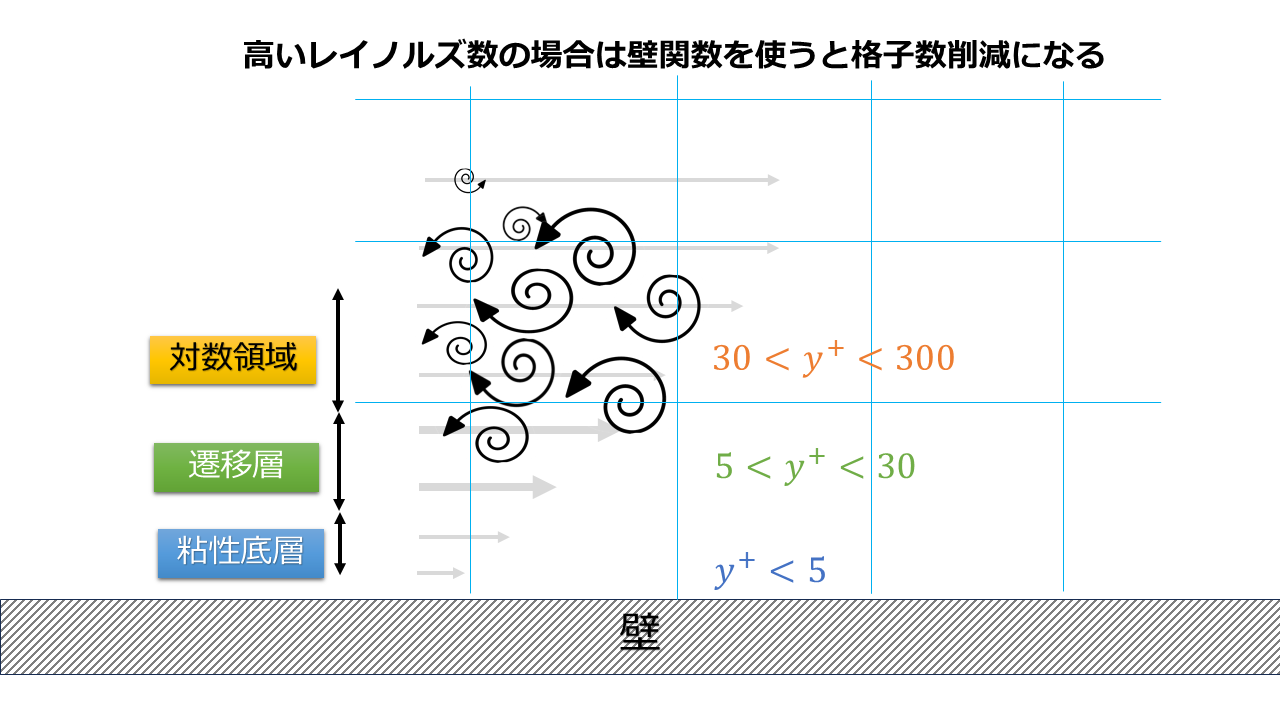
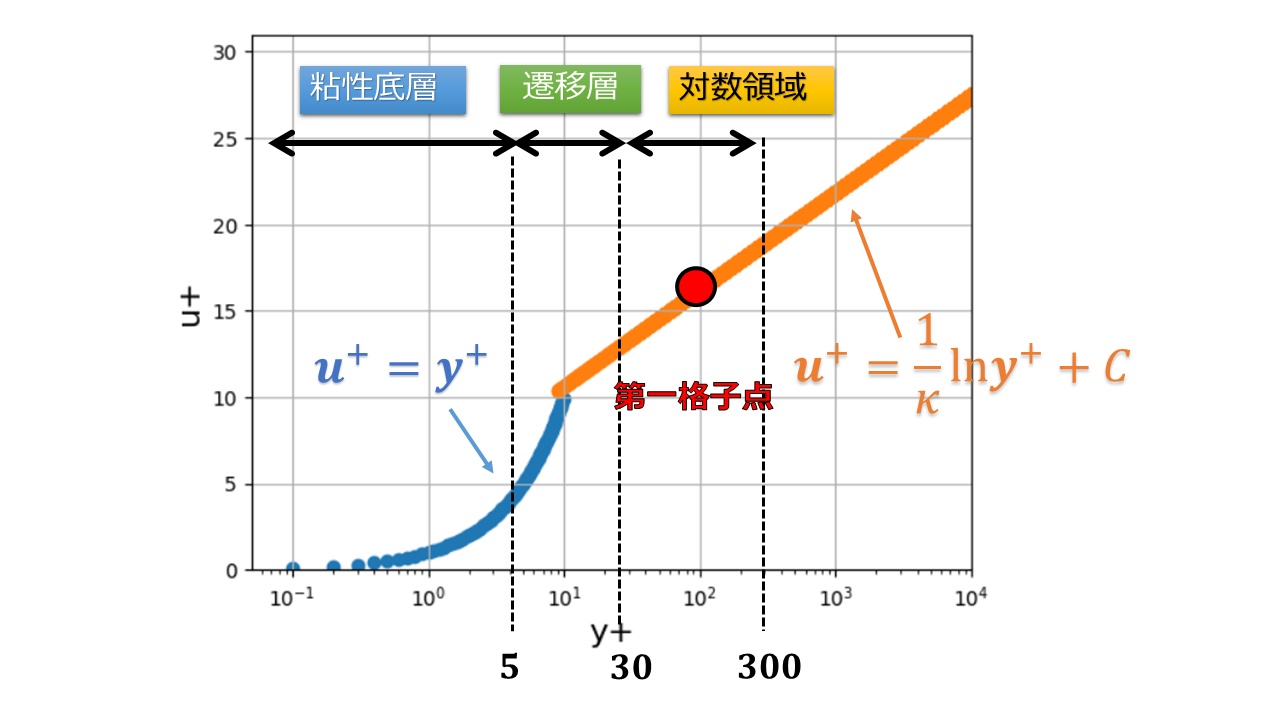
しかし、そんな都合よく$y^{+}$を30以上にできない場合がありますし、すべての壁面で$y^{+}$を30以上を目指すというのがそもそもできなかったりします。
なぜかは以下の式を見ればわかると思います。
- $y^{+}=\frac{u_{\tau}y}{\nu}$
- $u^{+}=\frac{u}{u^{\tau}}$
※$u_{\tau}=\sqrt{\frac{\tau_{w}}{\rho}}$：摩擦速度
※$\tau_{w}=\mu\frac{\partial u}{\partial y}$：壁面のせん断力
※$\kappa=0.41, C = 5.0$
$y^{+}=\frac{u_{\tau}y}{\nu}$より、$y^+$を大きくしようとした場合、壁面第一層はメッシュサイズを大きくする必要があり、スペース的にも形状の再現度からもできなかったりします。
そこでやむなく$y^{+}\sim 1$であっても、そのまま解析することもあります。
本記事での解析の内容
ここでは使用する乱流モデルとメッシュサイズ変更について触れておきます。
乱流モデル
乱流モデルにはさまざまな種類がありますが、その中でもよく使われるのが $k$-$\varepsilon$モデル と $k$-$\omega$モデル です。そして、これらの長所を組み合わせたのが $k$-$\omega$SSTモデル です。
簡単に違いをまとめるとこんな感じです。
| モデル | 特徴 | 適用する$y^+$の範囲 | 向いている用途 |
|---|---|---|---|
| $k$-$\varepsilon$ | 乱流の主流部分をうまく捉えられるが、壁面近くの低レイノルズ数領域では精度が低い | $y^+ > 30$（壁関数必須） | 遠方場の乱流解析（航空力学、外部流れ） |
| $k$-$\omega$ | 壁面近傍の流れをよく捉えられるが、自由流に対して敏感すぎる | $y^+ \sim 1$（壁関数不要） | 境界層解析（流体機械、内部流れ） |
| $k$-$\omega$ SST | 壁近くでは$k$-$\omega$、遠方では$k$-$\varepsilon$が働くハイブリッドモデル | $y^+ \sim 1$でも$y^+ > 30$でも適用可能 | 幅広い用途で安定した解析が可能 |
壁面近くでは流れが減速し、せん断力が大きくなるので、乱流の強さ（渦動粘性）を適切に減衰させる必要があります。
- $k$-$\varepsilon$モデル → 壁面ではそのまま使えないので 壁関数が必須
- $k$-$\omega$モデル → 低レイノルズ数モデルなので 壁面でもそのまま使える
- $k$-$\omega$SSTモデル → 壁近くでは$k$-$\omega$、遠方では$k$-$\varepsilon$が働くので、幅広い条件で使いやすい
つまり、$k$-$\omega$SSTは、壁面の影響を適切に考慮しながら、遠方場の乱流も正しく予測できる「バランスの取れたモデル」というわけですね。
OpenFOAMでの$k$-$\omega$SSTの概要はこちらをご参考ください。
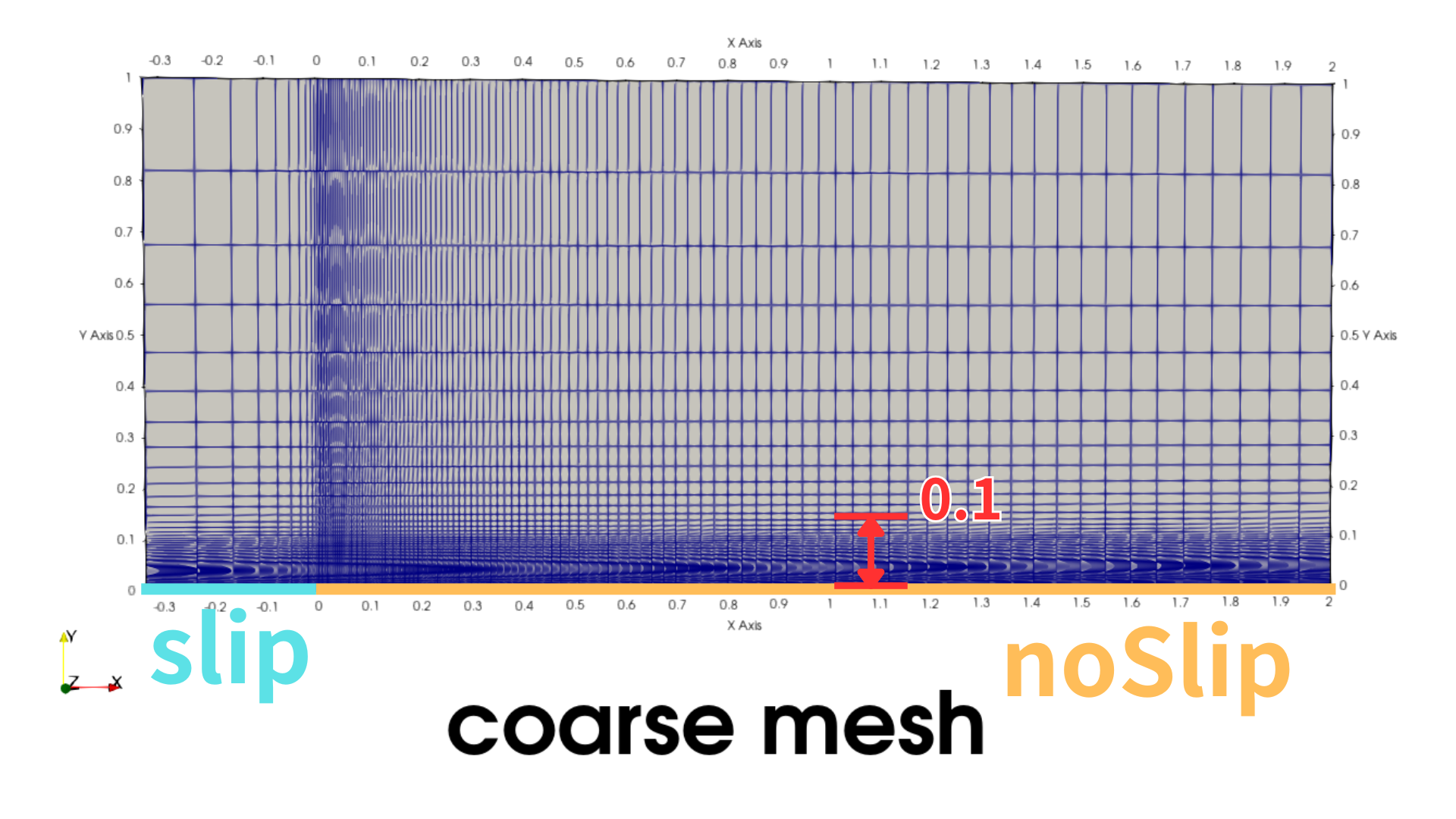
前回のメッシュサイズと今回のメッシュサイズ
前回のメッシュサイズと今回のメッシュサイズとを比較しておきます。
- 前回のメッシュサイズは$y^+>30$を目指すため粗め（coarse mesh）
- 今回は$y^+\sim 1$としたいため、メッシュを細かく(fine mesh)
どちらの動粘性係数も$\nu=2\times 10^{-7}$で流速は$U=1.0\text{m}/\text{s}$ですので、レイノルズ数は$R_e = \frac{U\,x}{\nu}$より助走距離に応じて変化しますが、〇〇あたりで乱流領域に到達します。
粗いメッシュ（coarse mesh）の場合は以下のような速度分布でした。
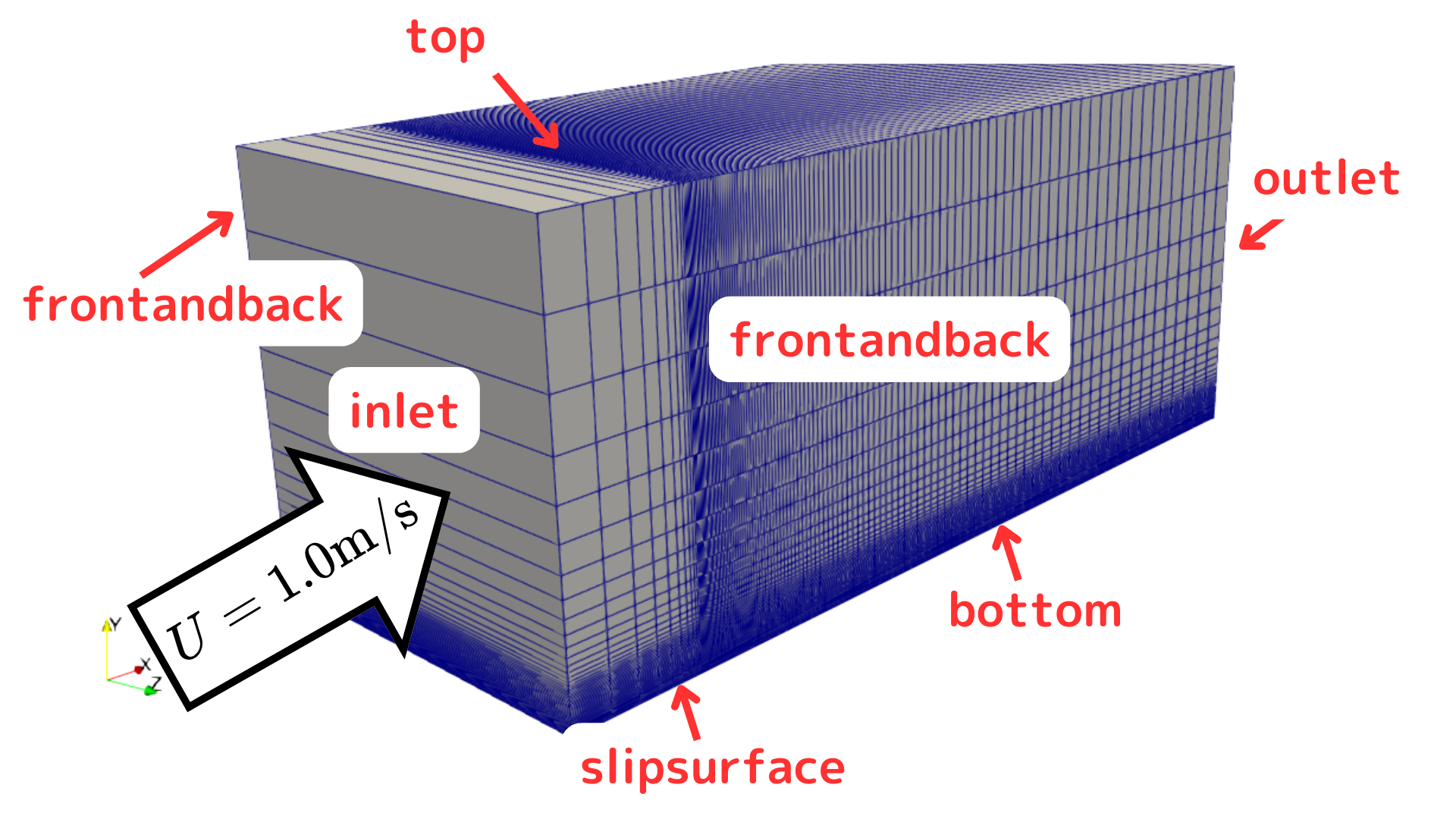
では、$y^+\sim 1$あたりになる、細かいメッシュで（fine mesh）ではどうでしょうか。
いくつかの解析設定で行います。
fine meshでの乱流モデルと壁関数の設定
| 乱流モデル | 壁関数$k$, $\omega$, $\nu_t$ | フォルダ名 |
| $k$-$\omega$SST | kqRWallFunction omegaWallFunction nutkWallFunction |
002_fine_kOmegaSST_nutkWF |
| ↑ | kqRWallFunction omegaWallFunction nutUSpaldingWallFunction |
002_fine_kOmegaSST_spalding |
| ↑ | fixedValue fixedValue calculated |
002_fine_kOmegaSST_NWF |
| 乱流モデル無し（laminar） | 設定必要なし | 002_fine_kOmegaSST_laminar |
境界条件の設定
corse meshでの設定から変更されるのは、0/k, 0/omega, 0/nutの境界名bottomだけが変わりますので、変更箇所の記載します。
まずメッシュ条件はsystem/blockMeshDictで設定しているため、メッシュ分割の設定変更を行います。
system/blockMeshDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
blocks ( /* hex (0 1 5 4 3 2 6 7) (100 1 50) simpleGrading (20 1 5) hex (11 0 4 10 9 3 7 8) (10 1 50) simpleGrading (0.05 1 5) hex (9 3 7 8 14 13 16 15) (10 1 18) simpleGrading (0.05 1 40) hex (3 2 6 7 13 12 17 16) (100 1 18) simpleGrading (20 1 40) */ hex (0 1 5 4 3 2 6 7) (100 1 225) simpleGrading (20 1 500) hex (11 0 4 10 9 3 7 8) (20 1 225) simpleGrading (0.05 1 500) hex (9 3 7 8 14 13 16 15) (20 1 10) simpleGrading (0.05 1 20) hex (3 2 6 7 13 12 17 16) (100 1 10) simpleGrading (20 1 20) ); |
以上のように$y$方向のメッシュ分割数を変えて細かいメッシュ設定にしています。
002_fine_kOmegaSST_nutkWF
壁関数に関してわかりやすい記事はこちらです。
0/k
|
1 2 3 4 5 6 |
bottom { //To use wall functions type kqRWallFunction; value $internalField; } |
kqRWallFunctionはzeroGradientのラッパーだと書かれています。
つまい、type zeroGradientと同じ設定をしているということですね。
0/omega
|
1 2 3 4 5 6 |
bottom { //Must be on - To enable wall function - Both values give right resutls type omegaWallFunction; value $internalField; } |
omegaWallFunctionの説明を少し書いておきます。
\omega_{\text{vis}} &= \frac{6 \nu_w}{\beta_1 y^2} \\
\omega_{\text{log}} &= \frac{\sqrt{k}}{C_\mu \kappa y} \\
G &= w(\nu_{{t}_{w}} + \nu_w) |\mathbf{n}\cdot (\nabla \cdot \mathbf{u})| C_\mu^{1/4} \frac{\sqrt{k}}{\kappa y} \quad \text{if} \quad y^+ > y^+_{\text{lam}}
\end{align*}
- $\omega = \text{Specific dissipation rate}$ [$\text{1}/\text{s}$]
- $\omega_{\text{vis}} = \omega \text{ computed by the viscous sublayer assumptions}$ [$\text{1}/\text{s}$]
- $\omega_{\text{log}} = \omega \text{ computed by the inertial sublayer assumptions}$ [$\text{1}/\text{s}$]
- $w = \text{Cell-corner weights}$ [-]
- $k = \text{Turbulent kinetic energy}$[$\text{m}^2/\text{s}^2$]
- $y = \text{Wall-normal distance}$ [$\text{m}$]
- $C_\mu = \text{Empirical model constant}$ [-]
- $\nu_w = \text{Kinematic viscosity of fluid near wall} $ [$\text{m}^2/\text{s}$]
- $\nu_{\text{tu}} = \text{Turbulent viscosity near wall}$ [$\text{m}^2/\text{s}$]
- $\mathbf{n} = \text{Face unit normal vector} $ [-]
- $\mathbf{u} = \text{Velocity}$ [$\text{m}/\text{s}$]
- $\kappa = \text{von Kármán constant}$[-]
wallFunctionCoefficients.C Source Fileの以下の部分で$y^{+}_{lam}$が決められています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
//- Estimate the y+ at the intersection of the two sublayers 38static scalar calcYPlusLam 39( 40 const scalar kappa, 41 const scalar E 42) 43{ 44 scalar ypl = 11; 45 46 for (int iter = 0; iter < 10; ++iter) 47 { 48 ypl = log(max(E*ypl, scalar(1)))/kappa; 49 } 50 51 return ypl; 52} 53 54} // End namespace Foam |
$\frac{1}{\kappa}\ln (Ey^+)=\frac{1}{0.41}\ln(9.8y^+)$の反復法で$y^+$を決定しており、$y^{+}=11.53$と決まります。
0/nut
|
1 2 3 4 5 |
bottom { type nutkWallFunction; value $internalField; } |
nutkWallFunctionの説明を少し書いておきます。
\nu_t &= f_{\text{blend}}(\nu_{\text{tvis}}, \nu_{\text{tlog}})\\
\nu_{\text{tvis}} &= 0\\ \nu_{\text{tlog}} &= \nu_w \left( \frac{y^+ \kappa}{\ln (E y^+) }-1 \right) \\
y^+ &= C_\mu^{1/4} \frac{y \sqrt{k}}{\nu_w}
\end{align*}
$k$から$\nu_t$を求めているということです。
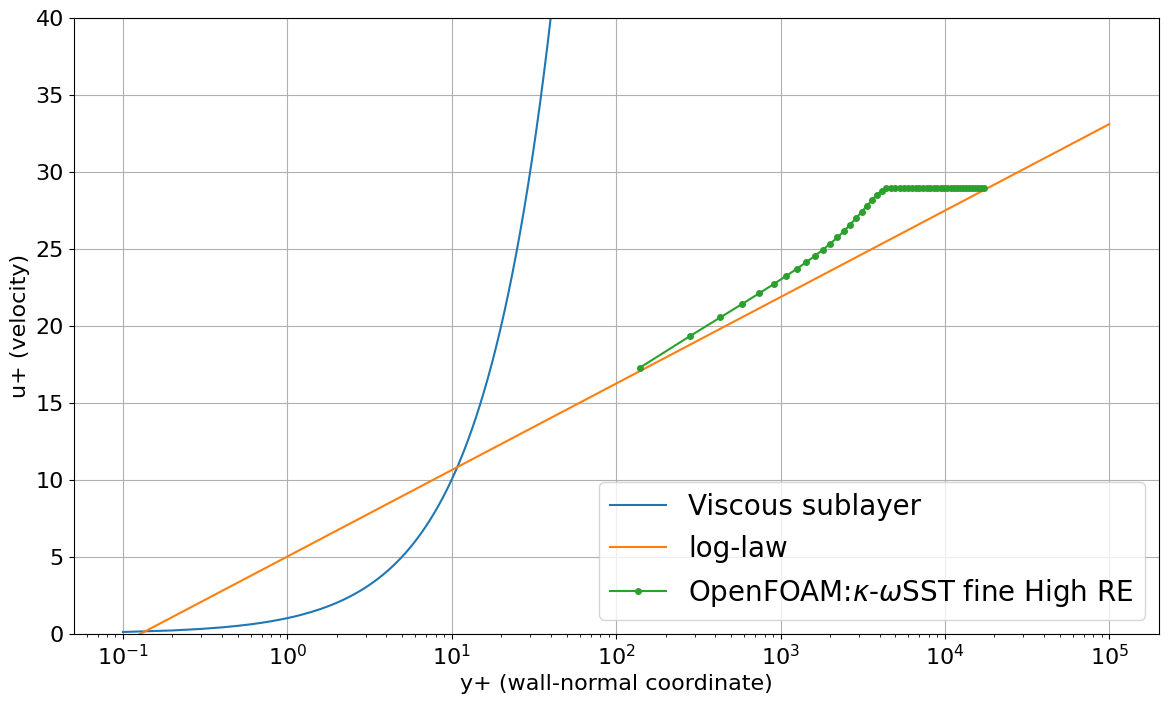
$x=1.90334$の位置で、$y$方向に$0~0.1$の物理量をサンプルとして出力し、$y^+$の値を計算することにします。
横軸$y^{+}$、縦軸u^{+}$にしたのが下のグラフです。
- Viscous sublayar：$u^{+}=y^{+}$
- log-law：$u^{+}=\frac{1}{\kappa}\log_{10}y^{+}+C$
※$\kappa=0.41, C = 5.0$
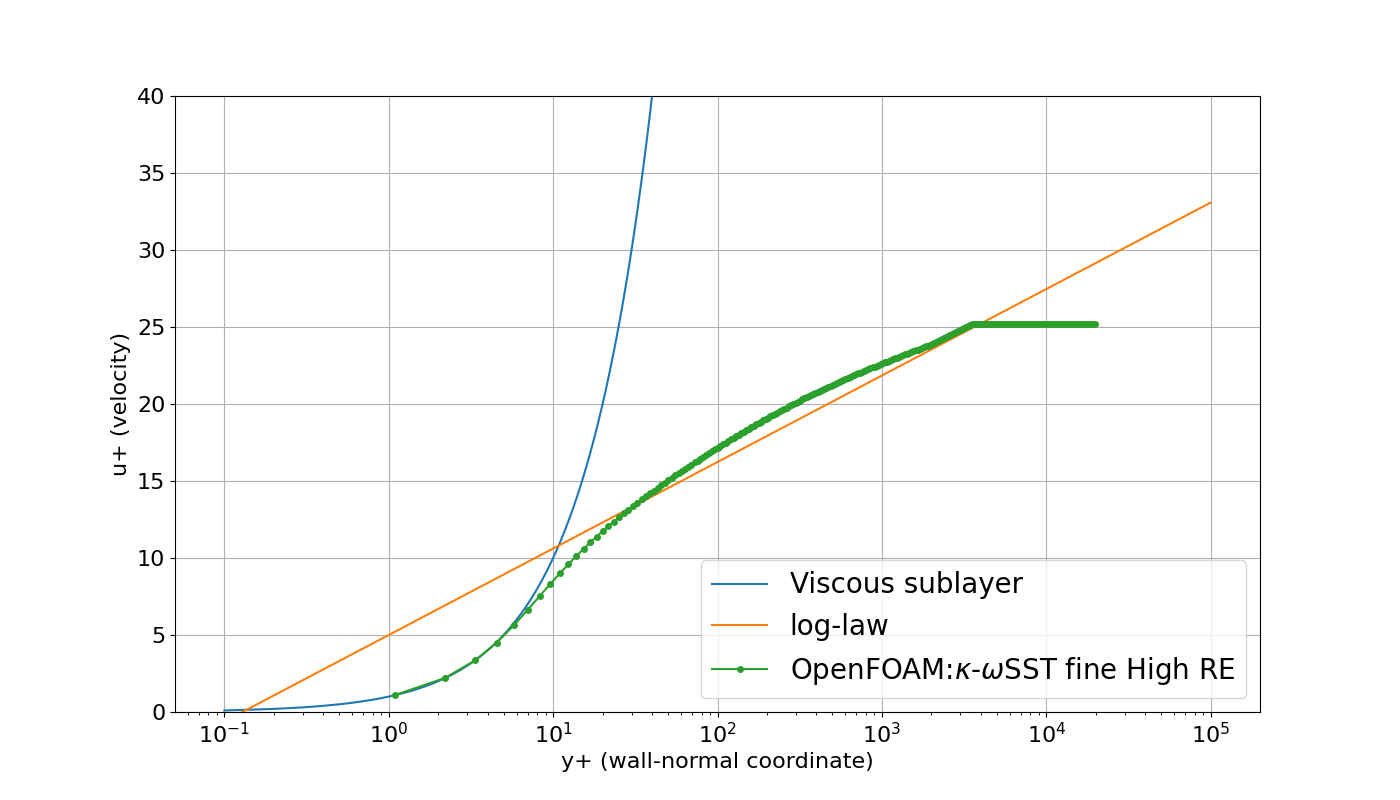
$y^+\sim 1$あたりからプロットされており、速度分布は層流域から乱流域までそこそこ線に乗っているのがわかります。
壁面のせん断力が0.00158117でした。
002_fine_kOmegaSST_spalding
0/k
|
1 2 3 4 5 6 |
bottom { //To use wall functions type kqRWallFunction; value $internalField; } |
0/omega
|
1 2 3 4 5 6 |
bottom { //Must be on - To enable wall function - Both values give right resutls type omegaWallFunction; value $internalField; } |
0/nut
|
1 2 3 4 5 |
bottom { type nutUSpaldingWallFunction; value $internalField;; } |
nutUSpaldingWallFunctionの説明を少ししておきます。
\nu_t &= \max \left( 0, \frac{u_{\tau}^2}{|\nabla \mathbf{u}| + \zeta} – \nu_w \right)\\
y^+ &= u^+ + \frac{1}{E} \left[ \exp(\kappa u^+) – 1 – \kappa u^+ – 0.5 (\kappa u^+)^2 – \frac{1}{6} (\kappa u^+)^3 \right]
\end{align*}
横軸$y^{+}$、縦軸u^{+}$にしたのが下のグラフです。
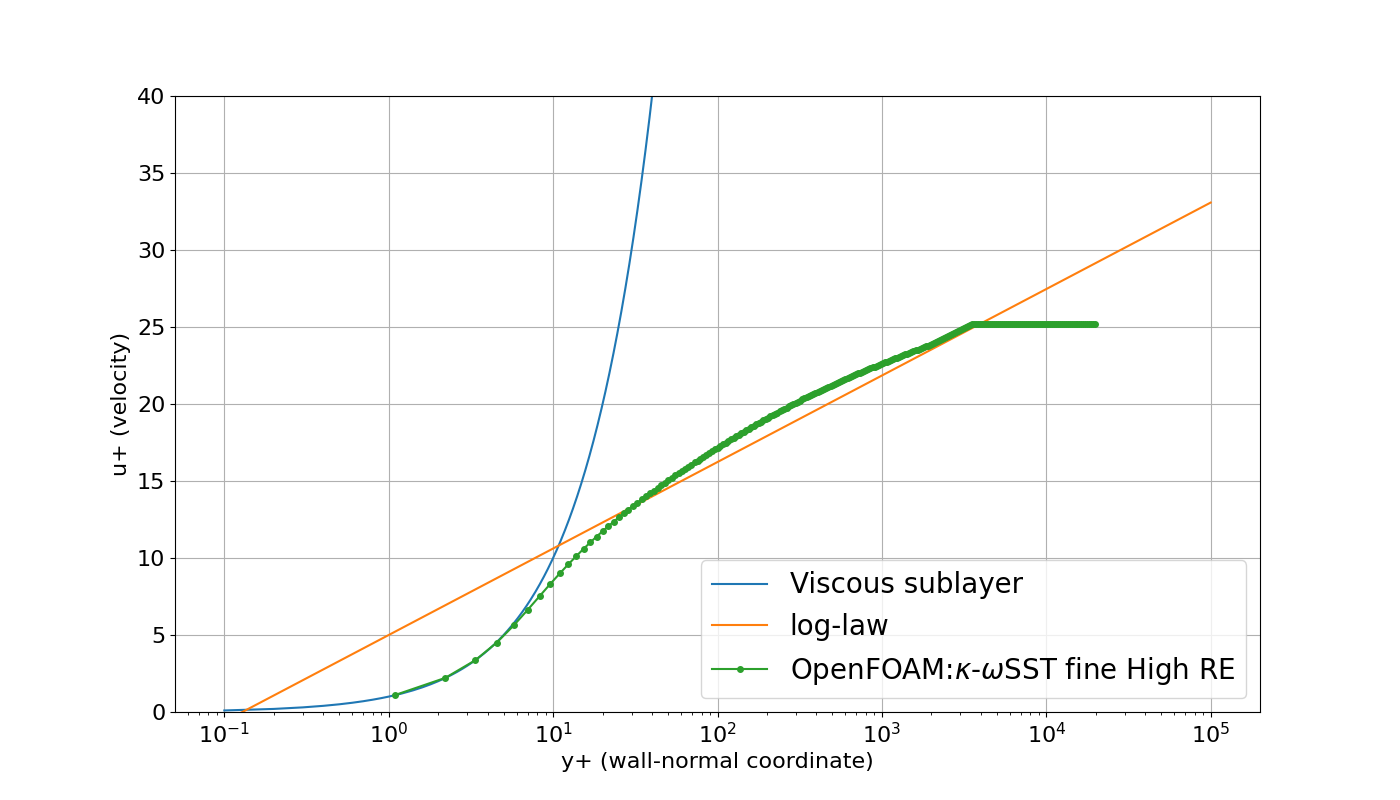
こちらもかわらず線に乗っています。$y^+\sim 1$あたりからプロットされており、速度分布は層流域から乱流域までそこそこ線に乗っているのがわかります。
壁面のせん断力が0.00158116でした。
002_fine_kOmegaSST_NWF
今度は壁関数を使わない設定で流体解析を行います。
0/k
|
1 2 3 4 5 |
bottom { type fixedValue; value $internalField; } |
0/omega
|
1 2 3 4 5 |
bottom { type fixedValue; value $internalField; } |
0/nut
|
1 2 3 4 5 |
bottom { type calculated; value uniform 0; } |
$\nu_t = a_1 \frac{k}{max(a_1 \omega , b_1 , F_{23}S)}$より求めるためcalculated; としています。
※こちら参照
横軸$y^{+}$、縦軸u^{+}$にしたのが下のグラフです。
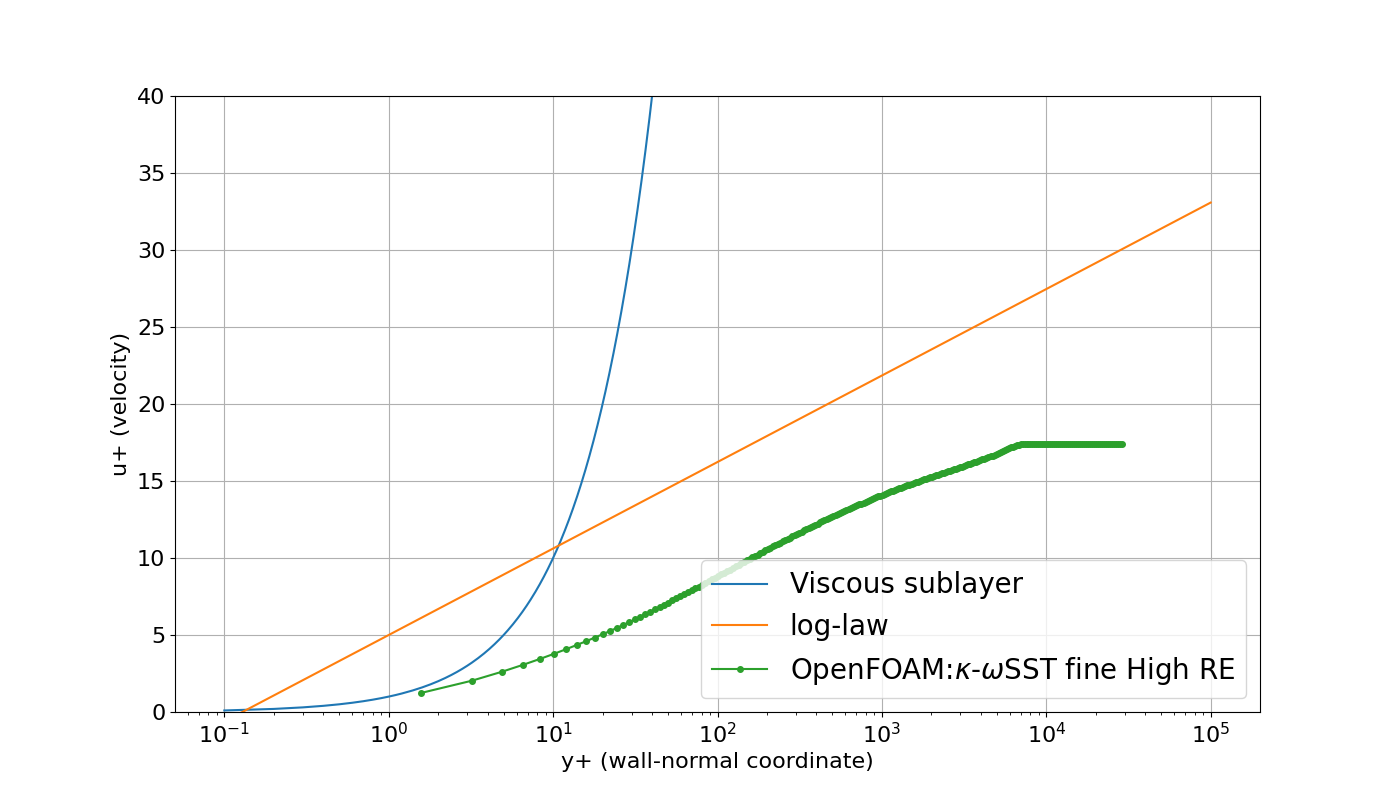
壁面のせん断力が0.00333268でした。
壁面せん断力が大きい値を示していますね。
- $y^{+}=\frac{u_{\tau}y}{\nu}$
- $u^{+}=\frac{u}{u^{\tau}}$
※$u_{\tau}=\sqrt{\frac{\tau_{w}}{\rho}}$：摩擦速度
※$\tau_{w}=\mu\frac{\partial u}{\partial y}$：壁面のせん断力
002_fine_kOmegaSST_laminar
今度は乱流モデル無しの設定にします。
constant/transportProperties
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
simulationType laminar; /* simulationType RAS; RAS { // Tested with kEpsilon, realizableKE, kOmega, kOmegaSST, // ShihQuadraticKE, LienCubicKE. RASModel kOmegaSST;//kEpsilon; turbulence on; printCoeffs on; } */ |
乱流モデル無しですので、0/k, 0/omega, 0/nutの設定は不要です。
横軸$y^{+}$、縦軸u^{+}$にしたのが下のグラフです。
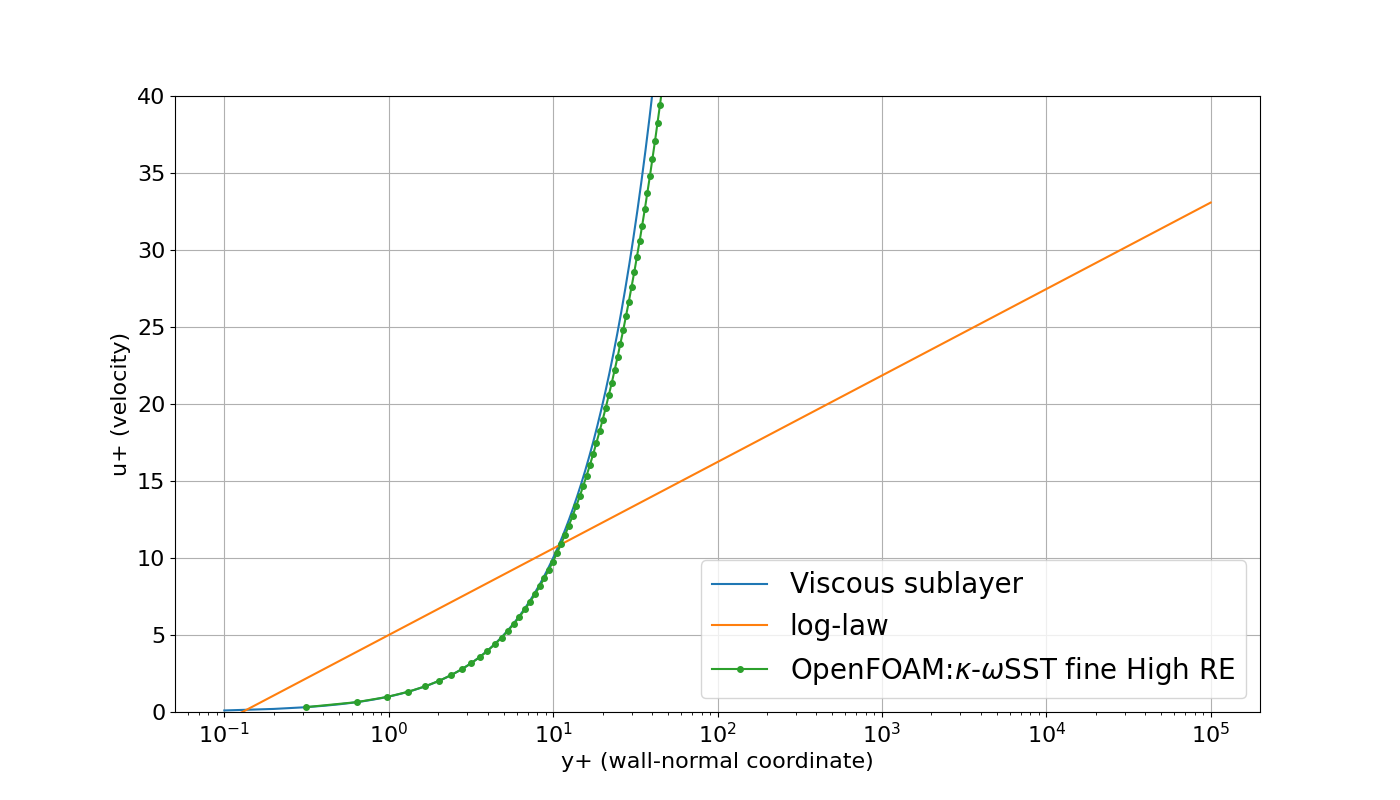
層流の速度分布$u^+$のまま伸びていますね。
ちなみに、壁面のせん断力が0.000131548でした。
今度は壁面せん断力がかなり小さい値を示していますね。
これより速度分布は流速がかなり速いというわけではなく、以下の式、
- $y^{+}=\frac{u_{\tau}y}{\nu}$
- $u^{+}=\frac{u}{u^{\tau}}$
より摩擦速度$u_{\tau}=\sqrt{\frac{\tau_w}{\rho}}$より、壁面せん断力$\tau_w$が小さくなった結果、無次元化した値の$y^+$小さくなり、流速$u^+$が大きくなってしまっているということです。
まとめ
今回の記事では、$y^+\sim 1$の条件下での平板流れ解析を行い、$k$-$\omega$ SSTモデルを用いた際の壁関数の影響を比較しました。その結果、壁関数の種類や有無によって壁面せん断力や速度分布が異なることが確認できました。
$k$-$\omega$SSTモデルは$y^+1$に関しては壁関数を使用する限りそれほど制限がない乱流モデルであることがわかりました。
とある資料にメモした pic.twitter.com/nSUijF5Na2
— カマキリ🐲CAE頑張る (@t_kun_kamakiri) June 14, 2023
次回は、$k$-$\varepsilon$モデルを用いて同様の解析を行い、今回の結果と比較してみます。$k$-$\varepsilon$モデルの特性を考慮しながら、どのような違いが現れるのかを詳しく見ていきましょう！引き続きOpenFOAMを活用した乱流解析を深めていきましょう！
計算力学技術者のための問題アプリ
計算力学技術者熱流体２級、1級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。
OpenFOAMに関する技術書を販売中！
OpenFOAMを自宅で学べるシリーズを販売中です。
OpenFOAM初学者から中級者向けの技術書となっていますので、ぜひよろしくお願いいたします。
次回の技術書典18に向けて内容を考え中です。
乞うご期待！！
お勧めの参考書
乱流モデルの数式の展開が非常に丁寧なのはこちらの参考書です。
今まで読んだ本の中で途中式もしっかり書いてあって一番丁寧でした。
乱流モデルの話だけでなく、混相流（気液、固液）や粒子法、浅水方程式の話も乗っているので重宝しています。
乱流モデルはこちらもお勧めです。
前半は数値シミュレーションの離散化の話で、後半に乱流モデルの話が出てきます。
乱流モデルのざっくりした解説と流体全般の基礎知識にはこちらがちょうど良いでしょう。
Follow @t_kun_kamakiri
