こんにちは(@t_kun_kamakiri)
今回の記事では2次元の円柱まわりの流れの流体解析の設定方法を示します。
2025年5月末の技術書典18に向けて、OpenFOAMを用いた熱流体解析のひとつのテーマとして円柱まわりの流れを考えています。
- 無限に長い円柱まわりの流れをOpenFOAMでシミュレーションする設定方法を示す
- 今回は乱流モデルを使用しないモデル(層流モデル)で解析結果を示す
OpenFOAM v2412(WSL2 Ubuntu 22.04)
【宣伝】2次元円柱内流れ(非圧縮流れ)
本代に入る前に少し宣伝ですが・・・本記事のメッシュ作成や解析設定について、基礎から学びたい方向けに、「2次元円柱内流れ(非圧縮流れ)」として、モデル作成からグラフ作成までの一連の流れをまとめたものを技術書としてまとめています。
技術書では以下の「2次元円柱内流れ(非圧縮流れ)」として、
- カルマン渦の生成
- レイノルズ数と抗力係数の関係
- レイノルズ数とストローハル数
- ポテンシャル流れと粘性流体の圧力係数の違い
- 力学的相似性
- Pythonを使ったパラメータスタディ
などなど、モデル作成からグラフ作成までの一連の流れをまとめたものを出しております。
ページ数は140ページです。
↓内容のチラ見せ
本書の解析モデルはgithubに置いているので、本書と照らし合わせながら読み進めることができます。
興味ある方はぜひ手に取ってみてください。
円柱周りの解析設定
使用するソルバはbuoyantSimpleFoam(浮力を考慮した定常の熱流体ソルバ)です。
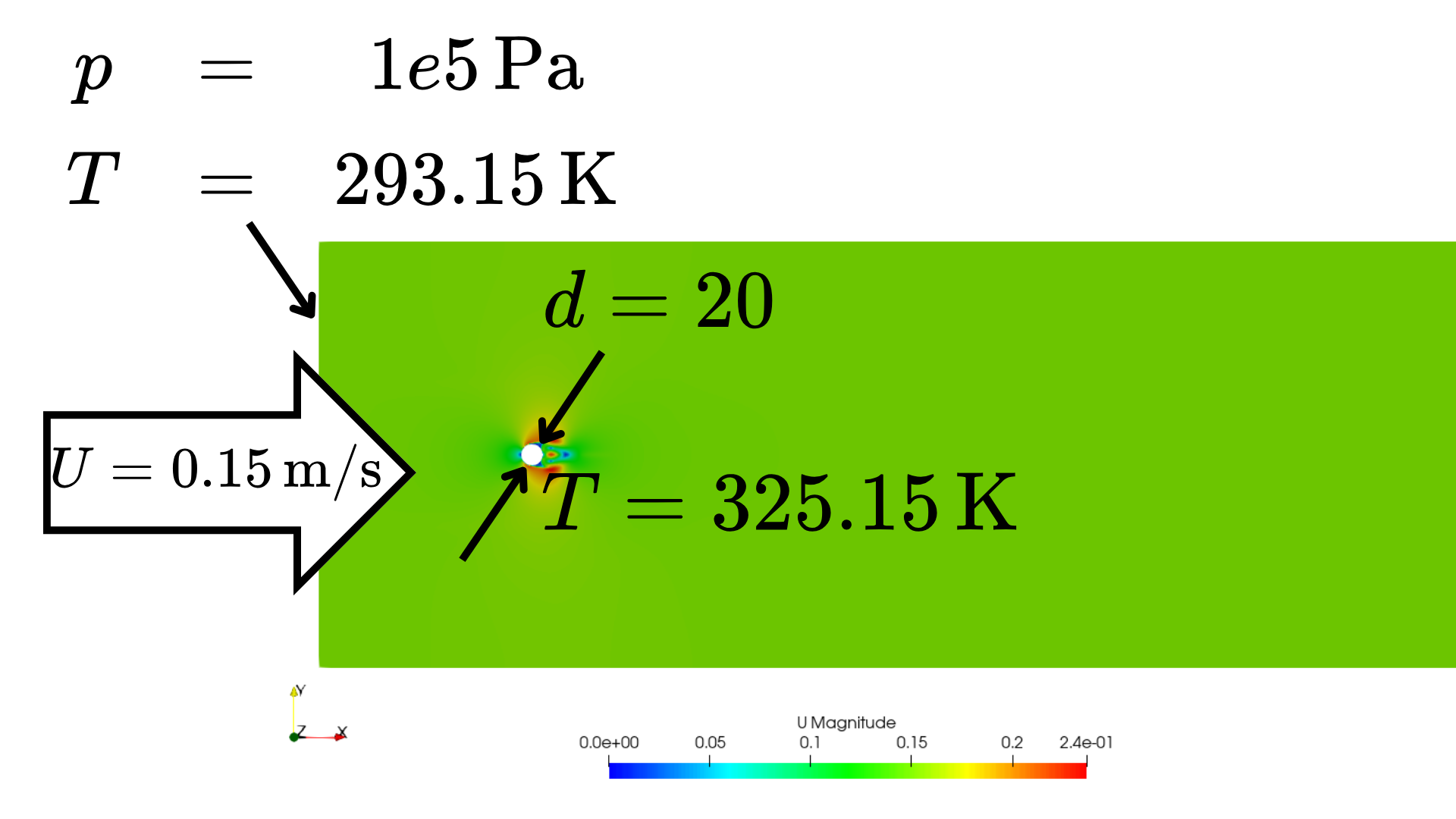

物性値
空気を想定していますが、値はキリの良い数値に変更しています。
- モル質量:28.0[g/mol]
- 定圧比熱:1000.0 [J/kg K]
- 粘性係数:1.8E-5 [Pa・s]
- プラントル数:0.7
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
thermoType { type heRhoThermo; mixture pureMixture; transport const; thermo hConst; equationOfState perfectGas; specie specie; energy sensibleEnthalpy; } mixture { specie { molWeight 28.0; } thermodynamics { Cp 1000.0; Hf 0; } transport { mu 1.8e-5; Pr 0.70; } } |
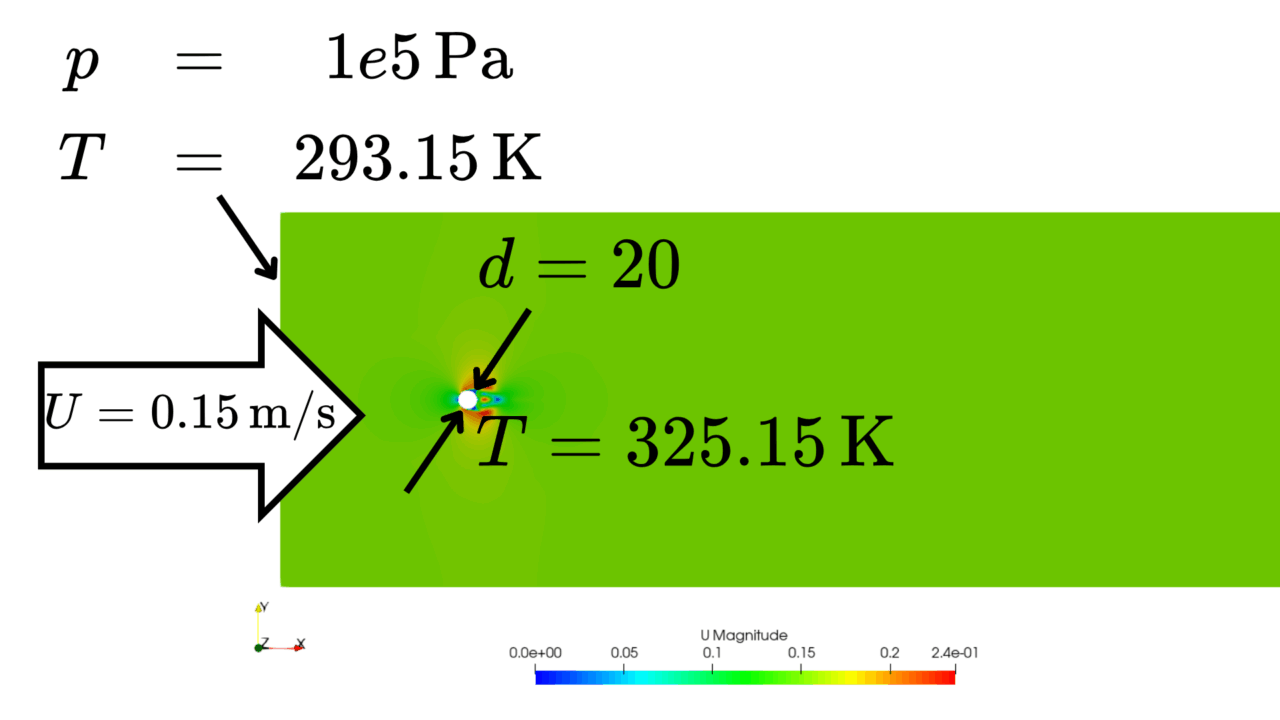
流入の流速が$U=0.15\,\text{m}/\text{s}$、円柱の直径が$d=20\,\text{mm}$であることから、レイノルズ数$Re$が求まります。
Re=\frac{Ud }{\mu/\rho}
\end{align*}
ただし、mixture pureMixture;としていることから、 $\rho$は理想気体の状態方程式$p=\rho R_{MW}T$から決まります。
$ R_{MW}$は気体定数と呼ばれ、気体ごとに決まる定数です。
具体的には一般気体定数$R$[J/mol K]とモル質量$MW$[kg/mol]を用いて、以下のように定義されています。
R_{MW}=\frac{R}{MW}=\frac{8.3145}{28.0E-3}=296.95\, \text{J}/\text{kg K}
\end{align*}
ということなので、密度は次式で求まります。
\rho=\frac{p}{R_{MW}T}=\frac{1E5}{296.95\times 293.15}=1.148\,\text{kg}/\text{m}^3
\end{align*}
この値を用いるとレイノルズ数$Re$が求まります。
Re=\frac{Ud }{\mu/\rho}=\frac{0.15\times 20R-3}{1.8E-5/1.148}=191
\end{align*}
レイノルズ数から判断すると、流れの様子は非定常のカルマン渦列が生成する流れということがわかります。



大小全ての渦をメッシュサイズで再現するか、乱流モデルを導入するか選択が難しいところですが、いちおうカルマン渦列は層流の部類として扱うことにします。
渦が時刻歴の変化に伴って上下から生成することから、非定常性がある現象だということがわかります。
解析設定としては非定常解析、層流モデル・・・としたいところですが、いきなり非定常の解析を行うのは計算コストがかかるので、今回は定常解析で行うこととします。
ゆえに、以下の設定で行うことにします。
- 定常解析
- 層流モデル(乱流モデル無し)
- 重力の設定は無し
境界条件
乱流モデルを使用しないとなると、境界条件で使用するファイルは0/U, 0/T, 0/p_rgh, 0/pになります。
p_rghは静圧から流体質量による圧力分を差し引いた量$p_{rgh}=p-rgh$なので、0/pは0/p_rghから計算され設定にします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
dimensions [ 0 1 -1 0 0 0 0 ]; internalField uniform (0.15 0 0); boundaryField { Xmin { type fixedValue; value $internalField; } Xmax { type zeroGradient; } "(Ymin|Ymax)" { type slip; } hole { type noSlip; } empty { type empty; } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
dimensions [1 -1 -2 0 0 0 0]; internalField uniform 1e5; boundaryField { Xmin { type zeroGradient; } Xmax { // type fixedValue; // value $internalField; // type fixedFluxPressure; // value uniform 1e5; type totalPressure; U U; phi phi; psi none; gamma 1; rho rho; p0 uniform 1e5; } "(Ymin|Ymax)" { type slip; } hole { //type zeroGradient; type fixedFluxPressure; value uniform 1e5; } empty { type empty; } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
dimensions [1 -1 -2 0 0 0 0]; internalField uniform 1e5; boundaryField { Xmin { type calculated; value $internalField; } Xmax { type calculated; value $internalField; } "(Ymin|Ymax)" { type calculated; value $internalField; } hole { type calculated; value $internalField; } empty { type empty; } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
dimensions [0 0 0 1 0 0 0]; internalField uniform 293.15; // 20 degC boundaryField { Xmin { type fixedValue; value $internalField; } Xmax { type zeroGradient; } "(Ymin|Ymax)" { type slip; } hole { type fixedValue; value uniform 325.15; // 50 degC } empty { type empty; } } |
結果
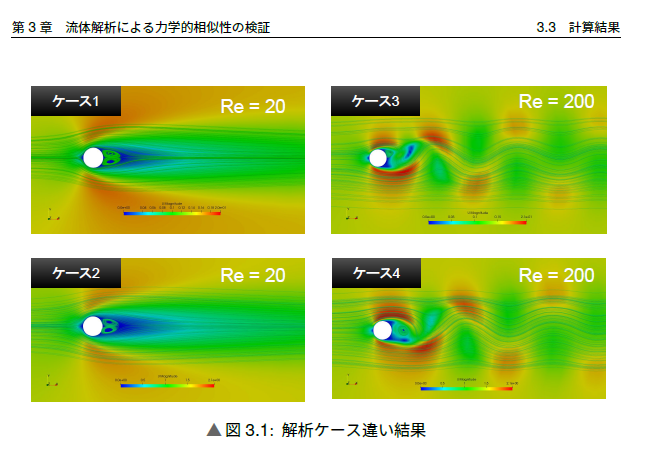
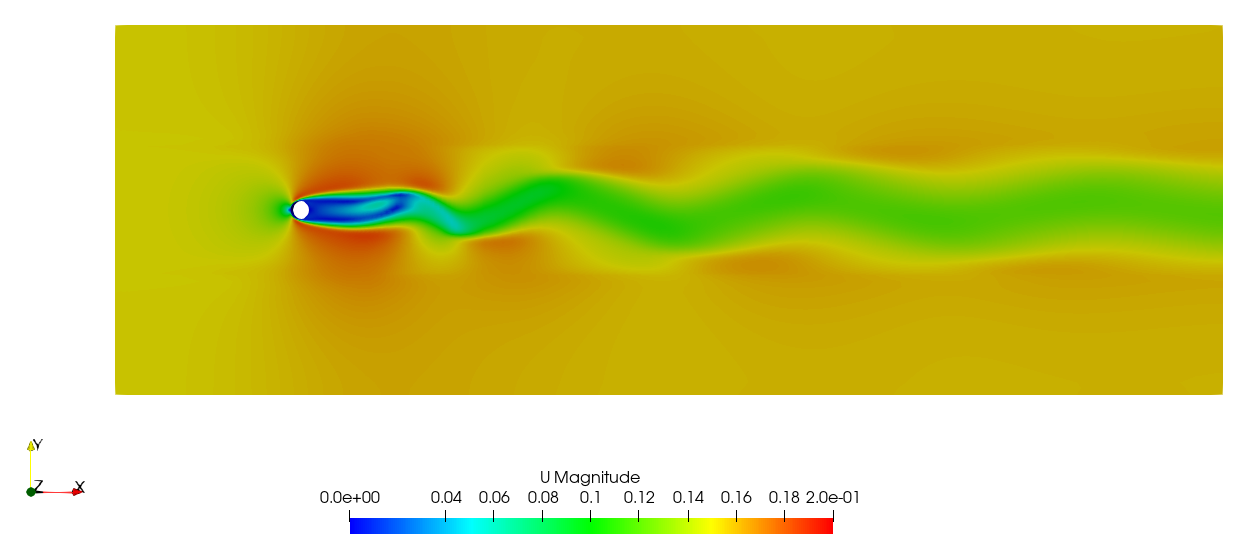
こちらが流速分布になります。
非定常性のあるカルマン渦列に対して、今回は定常解析を行ったために、流速分布がじゃっかんなまっている感じがします。

抗力係数
レイノルズ数$Re=200$に対して、円柱まわりの抗力係数は$Cd=1.5$程度というのが知られていますが、結果は以下のようになっています。
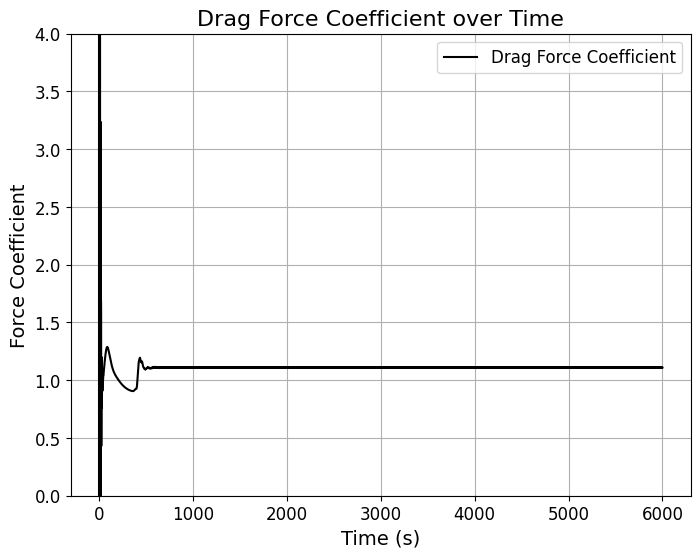
非圧縮流れの例ではありますが、非定常解析で抗力係数が文献値通りの$Cd=1.5$になる結果は、技術書典17で販売している技術書にて記載しています。
ヌセルト数
ヌセルト数はどうでしょうか。
ヌセルト数とは、熱対流の強さを評価する無次元数で$\text{ヌセルト数} = \frac{対流による伝熱}{熱伝導による伝熱}$と定義されています。
具体的な式では、$Nu=\frac{h d}{\lambda}$と定義されます。
- 熱伝達率$h$は、OpenFOAMで円柱まわりの熱流束$\dot{Q}$を出力し、熱伝達率の定義式$h=-\frac{\dot{Q}}{A(T_{ref}-T_{w})}$で算出
- プラントル数$Pr=\frac{\mu C_{p}}{\lambda}$より、熱伝導率$\lambda$は$\lambda=\frac{\mu C_{p}}{Pr}$で算出
上記を考慮したPythonプログラムを作成するとOpenFOAMよりヌセルト数が求まります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
import matplotlib.pyplot as plt import numpy as np # 定数の設定 d = 20/1000 Lz =10/1000 Tref = 273.15 +20 Tw = 325.15 #273.15 +50 # 面積 Area = np.pi*d*Lz Uref = 0.15 pref = 1E5 Tref = 293.15 R = 8.3145 MW = 28.0E-3 # kg/mol RMW = R/MW # J/(mol*K) rho = pref/(RMW *Tref) mu = 1.8e-5 nu = mu/rho #熱物性 Cp = 1000 Pr = 0.7 lambdaf = mu*Cp/Pr # データの読み込み data = pd.read_csv( "postProcessing/wallHeatFlux/0/wallHeatFlux.dat", sep=r"\s+", comment="#", names=["Time", "patch", "min", "max", "Integral"] ) dotQ = data["Integral"].iloc[-1] heatcoeff = -dotQ/Area/(Tref-Tw) Re = Uref*d/(mu/rho) print(f"熱伝達率:{lambdaf}") print(f"熱量:{dotQ}") print(f"熱流束:{dotQ/Area}") print(f"熱伝達率:{heatcoeff}") print(f"密度:{rho}") print(f"レイノルズ数:{Re}") # レイノルズ数範囲の定義 Re_ranges = [(0.4, 4), (4, 4e1), (4e1, 4e3), (4e3, 4e4), (4e4, 4e5)] C_values = [0.989, 0.911, 0.689, 0.193, 0.027] m_values = [0.330, 0.385, 0.466, 0.618, 0.805] # レイノルズ数の配列を作成 Re_all = np.logspace(np.log10(0.4), np.log10(4e5-1), 100) Nu_all = np.zeros_like(Re_all) # ヌセルト数の計算 for (Re_min, Re_max), C, m in zip(Re_ranges, C_values, m_values): Re_mask = (Re_all >= Re_min) & (Re_all <= Re_max) Nu_all[Re_mask] = C * Re_all[Re_mask]**m * Pr**(1/3) # サンプルのレイノルズ数とそれに対応するヌセルト数の計算 Re_sample = np.array([Uref*d/nu]) # プロットしたいReの点 Nu_sample = np.zeros_like(Re_sample) for i, Re in enumerate(Re_sample): Nu_sample[i] = heatcoeff*d/lambdaf print(f"ヌセルト数:{Nu_sample[i]}") # グラフの描画 plt.figure(figsize=(10, 6)) plt.plot(Re_all, Nu_all, label='$Nu_{d.m}=CRe_d^n Pr^{1/3}$') plt.scatter(Re_sample, Nu_sample, color='red', zorder=5, label='Sample Points (Re, Nu)') plt.xlabel('Re (Reynolds Number)', fontsize=14) plt.ylabel('Nu (Nusselt Number)', fontsize=14) plt.title('Nusselt Number vs Reynolds Number', fontsize=16) plt.xscale('log') plt.yscale('log') plt.legend(loc='best') plt.ylim([0.1,1000]) plt.grid(True, which="both", ls="--") plt.show() |
ここでOpenFOAMで得られた結果と文献値との比較を行っています。
ヌセルト数とレイノルズ数の関係式($Nu = C \cdot Re^m \cdot Pr^{1/3}$)
※🔍 備考:この関係は、2次元円柱周りの外部流(非圧縮性・定常)での平均ヌセルト数に対する代表的な経験式の1つです。
| レイノルズ数の範囲 $Re$ | 関係式($Pr=0.7$を代入済) |
|---|---|
| $0.4 \leq Re < 4$ | $Nu = 0.989 \cdot Re^{0.330} \cdot 0.7^{1/3}$ |
| $4 \leq Re < 40$ | $Nu = 0.911 \cdot Re^{0.385} \cdot 0.7^{1/3}$ |
| $40 \leq Re < 4000$ | $Nu = 0.689 \cdot Re^{0.466} \cdot 0.7^{1/3}$ |
| $4000 \leq Re < 40000$ | $Nu = 0.193 \cdot Re^{0.618} \cdot 0.7^{1/3}$ |
| $40000 \leq Re < 400000$ | $Nu = 0.027 \cdot Re^{0.805} \cdot 0.7^{1/3}$ |
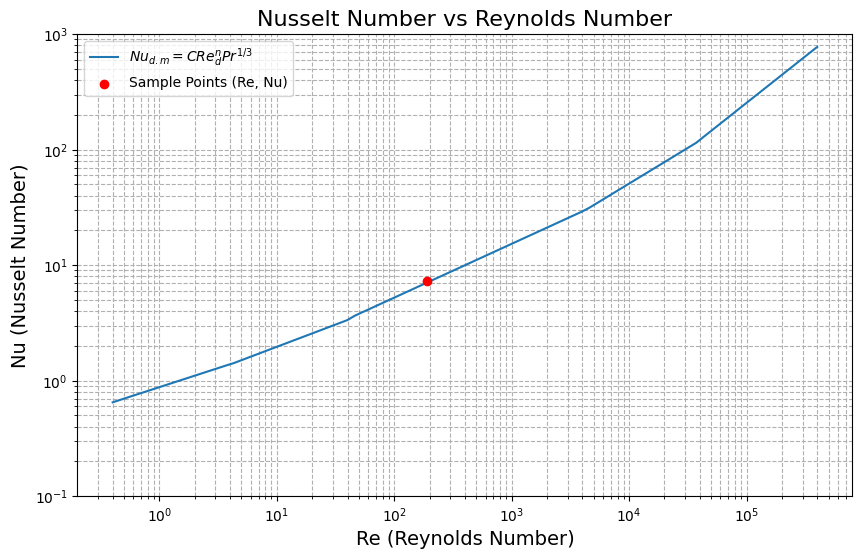

いくつか異なるレイノルズ数(今回は粘性係数を変更)で解析を行いましたが、概ね文献値通りになっています。
✅円柱まわりの流れ(Pr=0.7)
定常解析、乱流モデル無しでもここまで合うけど、Pr=7とかにすると温度境界層が小さくなって、メッシュサイズ次第で結果が変わりやすいのかな…
定常解析だとさすがに抗力係数は理論値からずれる(低めに出してしまう) pic.twitter.com/8rmjUMz0sG— カマキリ🐲技術書典18 (@t_kun_kamakiri) May 3, 2025
ネットを調べるとヌセルト数の計算をOpenFOAMで実装している人がいます。
局所ヌセルト数とか計算できるのでしょうか…
まとめ
今回は2次元の円柱まわりの解析の設定を行い、抗力係数やヌセルト数が文献値に一致するかを確認しました。
レイノルズ数$Re=200$の非定常性のあるカルマン渦列に対して、定常解析で行うと抗力係数は低めに出て、ヌセルト数はそれほど変わらないという結果でした。
今回はプラントル数$Pr=0.7$ということもあって、$Pr=\frac{速度境界層}{温度境界層}$から、温度境界層がそれほど小さくないと言えます。
つまり、ヌセルト数がそれほど文献値とずれなかったのは、温度に関係する熱量などがメッシュサイズや非定常性などにはあまり影響されにくかっただけということにが考えられます。
技術書典18では、本記事の「2次元円柱まわりの熱流体解析」やそのほかの熱流体のテーマを取り扱う予定です。
次回の技術書典18に向けて内容を考え中です。
乞うご期待!!

計算力学技術者のための問題アプリ
計算力学技術者熱流体2級、1級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。
OpenFOAMに関する技術書を販売中!
OpenFOAMを自宅で学べるシリーズを販売中です。
OpenFOAM初学者から中級者向けの技術書となっていますので、ぜひよろしくお願いいたします。
お勧めの参考書
本記事の内容について触れている書籍がこちらです。
CFD(流体解析)のガイドブックというタイトルだけあって、熱流体に関する内容は網羅的に書かれています。
乱流モデルの数式の展開が非常に丁寧なのはこちらの参考書です。
今まで読んだ本の中で途中式もしっかり書いてあって一番丁寧でした。
乱流モデルの話だけでなく、混相流(気液、固液)や粒子法、浅水方程式の話も乗っているので重宝しています。
乱流モデルはこちらもお勧めです。
前半は数値シミュレーションの離散化の話で、後半に乱流モデルの話が出てきます。
乱流モデルのざっくりした解説と流体全般の基礎知識にはこちらがちょうど良いでしょう。