こんにちは(@t_kun_kamakiri)
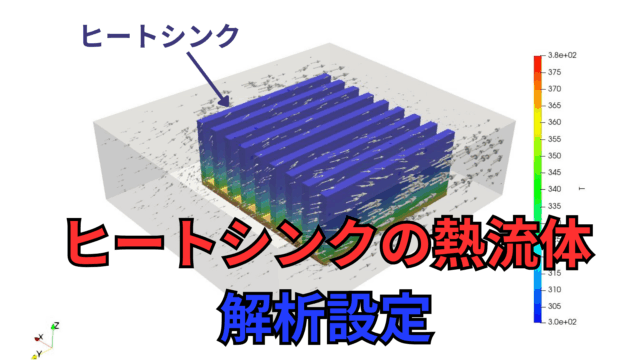
今回の記事では円管内の流れの流体解析の設定方法を示します。
2025年5月末の技術書典18に向けて、OpenFOAMを用いた熱流体解析のひとつのテーマとして円管内の流れを考えています。
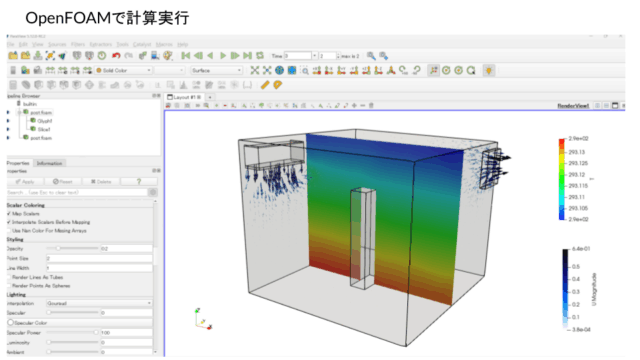
前回の記事では円管内の流れの熱流体解析を実施し、温度分布を可視化しました。
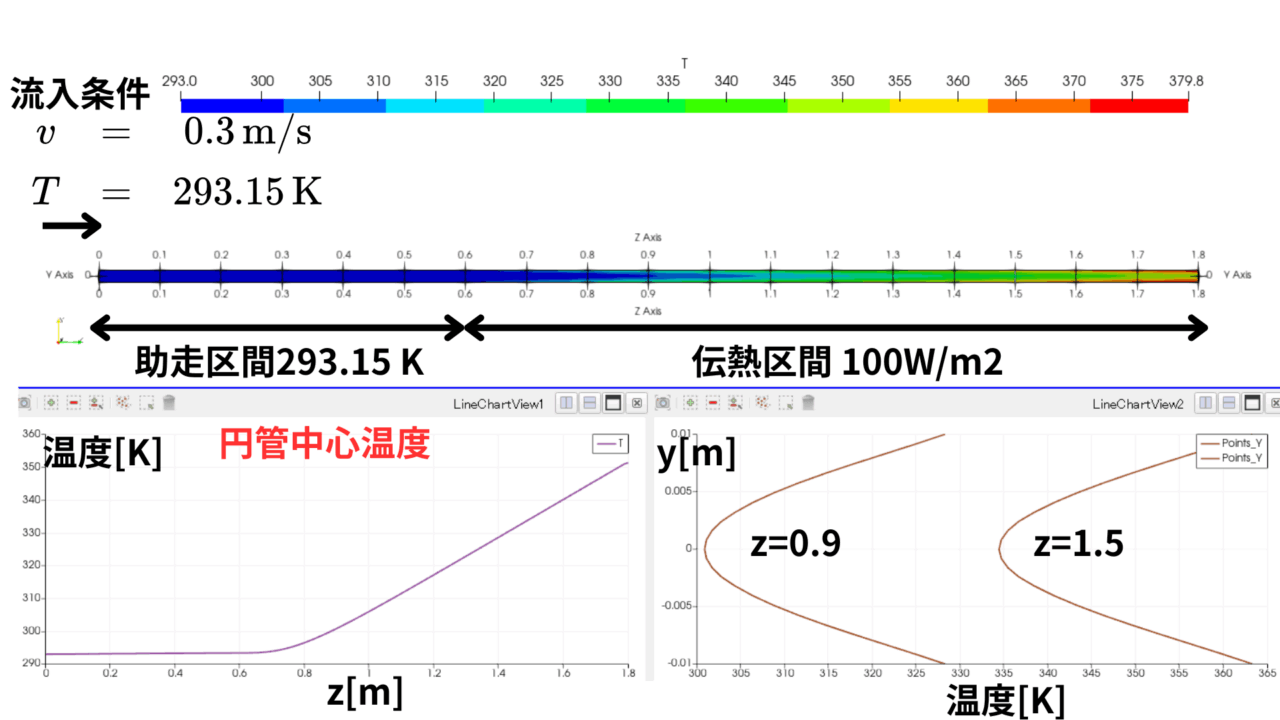
今回の記事では、以下の内容を取り扱います。
- OpenFOAMのcodedFunctionObjectを使って混合平均温度を算出するプログラムを作成する
- 混合平均温度と壁面温度の理論計算とOpenFOAMとの結果を比較する
OpenFOAM v2412(WSL2 Ubuntu 22.04)
【宣伝】円管内流れ(非圧縮流れ)
本代の円管内の流れの解析設定に入る前に宣伝になります。
本記事のメッシュ作成や解析設定について、基礎から学びたい方向けに、「円管内流れの層流解析」として、モデル作成からグラフ作成までの一連の流れをまとめたものを技術書としてまとめています。
ページ数は136ページです。
技術書では以下の内容を取り扱っています。
- 円管内流れ(層流)の速度分布の理論
- OpenFOAMで円管内流れの解析(blockMesh)
- OpenFOAMで円管内流れの解析(snappyHexMesh)
↓内容のチラ見せ
本書の解析モデルはgithubに置いているので、本書と照らし合わせながら読み進めることができます。
興味ある方はぜひ手に取ってみてください。
混合平均温度:円管内の流れ
円管内層流流れのヌセルト数は一定値であることが知られています。
- 壁面熱流束が一定の場合:$Nu=4.36$
- 壁面温度一定の場合:$Nu=3.66$
ここで、「あーなるほど、ヌセルト数がわかると$Nu=\frac{hd}{\lambda}$などから、熱伝達率$h=\frac{Nu\,\lambda}{d}$がわかるのか」….となるかというと、そう一筋縄ではいかないのです。
✅CFDで移動現象論111例題- Ansys Fluentによる計算解法 –
これどうやって混合平均温度計算しているのかと思って確認したら強引に求めてた。https://t.co/3OrHCOf3KK pic.twitter.com/GB7UJs0kq0— カマキリ🐲技術書典18 (@t_kun_kamakiri) May 5, 2025
ここにも記載しているよ円管内の流れにおいて熱流束$\dot{q}=-h(T_w-T_m(z))$という形で、混合平均温度$T_m(z)$を用いて、ヌセルト数一定値を導出しています。
混合平均温度
T_m &= \frac{\int_A \rho C_p u T \, dA }{ \int_A \rho C_p u \, dA }\\
&= \frac{ \int_0^{R} \rho C_p u(r) T \, 2\pi r\,dr}{ \int_0^R \rho C_p u(r) \, 2\pi r\,dr}
\end{align*}
- $\rho$:密度
- $u$:流速
- $T$:温度
- $A$:管断面積
- $C_p$:定圧比熱
混合平均温度は単位時間当たりに輸送するエネルギーから平均温度を温度を算出する式を意味します。
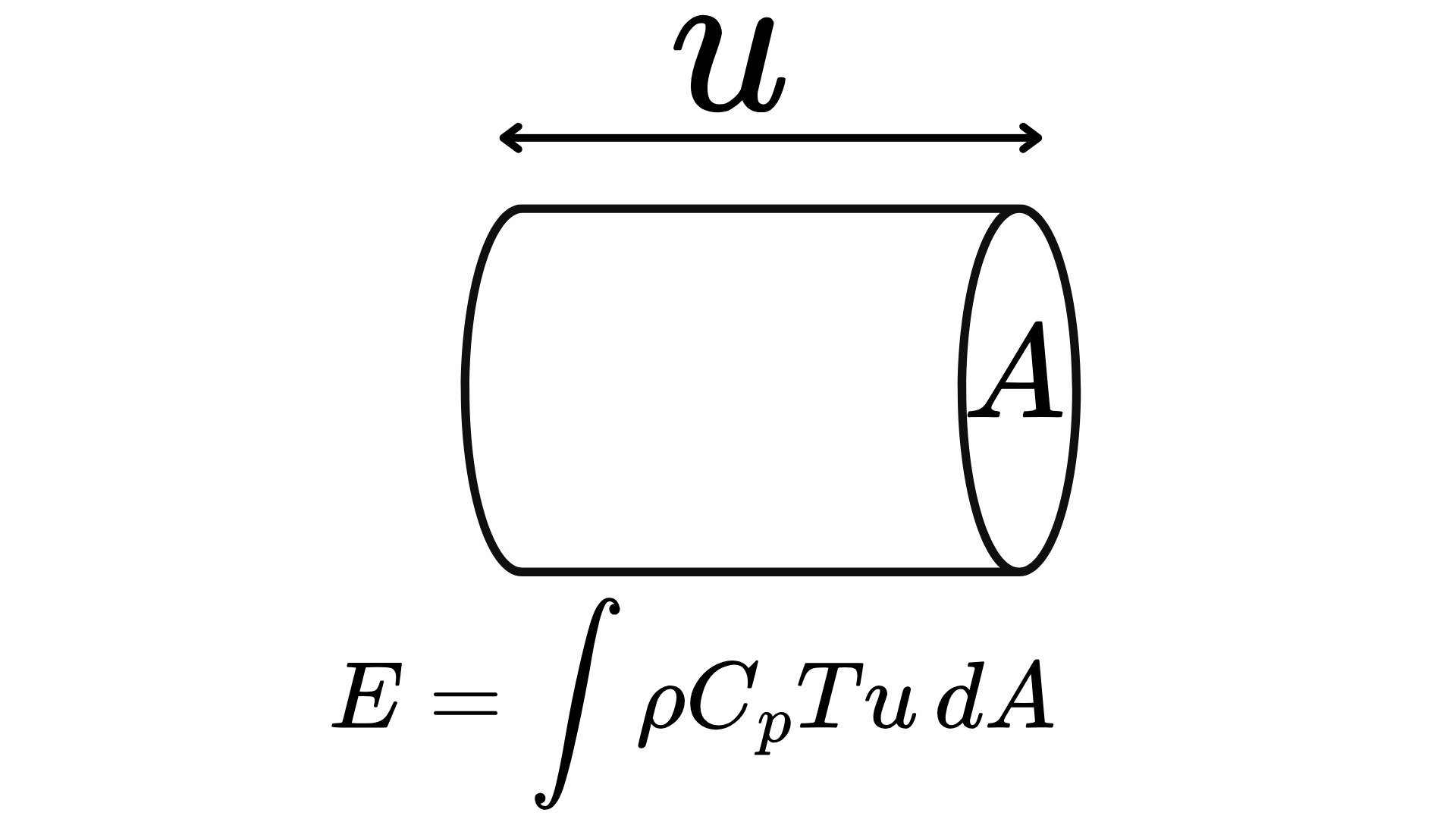
円管内流れ(層流)の速度分布
u(r) = u_{\mathrm{max}} \left( 1 – \left( \frac{r}{R} \right)^2 \right)
\end{align*}
詳しく学びたい方向けに参考書を紹介しておきます。
壁面の熱収束一定の場合
壁面が熱流束一定の場合と温度一定の場合でヌセルト数の導出過程が異なりますが、今回OpenFOAMで行うのは熱流束一定場合です。
まず大前提として混合平均温度は$T_m = \frac{ \int_0^{R} \rho C_p u(r) T \, 2\pi r\,dr}{ \int_0^R \rho C_p u(r) \, 2\pi r\,dr}$、層流流れの十分発達した速度分布を$u(r) = u_{\mathrm{max}} \left( 1 – \left( \frac{r}{R} \right)^2 \right)$であるとすると、混合平均温度は$z$方向に対して、
混合平均温度
T_m(z)=T_m(z_0)+\frac{2\dot{q}(z-z_0)}{\rho C_p R u_{\mathrm{max}}}
\end{align*}
と求められます。
さらに壁面温度$T_w(z)$は、
壁面温度
T_w(z)=T_m(z)+\frac{\dot{q}d}{Nu\lambda}
\end{align*}
と求められます。
- 壁面一定熱流束:$\dot{q}$
- 熱伝導率:$\lambda$
- ヌセルト数:$Nu=\frac{48}{11}$
- 円管直径:$d$
問題は混合平均温度$T_m$をどうやって求めるかというところです。
OpenFOAMのcodedFunctionObjectを使って混合平均温度を算出するプログラムを作成することにします。
混合平均温度を出力
OpenFOAMの標準機能で混合平均温度$T_m$を出力できないので、自分でプログラムを作成し混合平均温度のデータを出力してPythonでグラフ化することにします。
今の時代はChatGPTが優秀するぎるので、コードを生成してもらうことにします。
とはいえ、そんな簡単にはプログラムを生成してくれませんので、過去に作成したプログラムを参考にしてもらいながら、自ら監修に入って修正し、ようやくプログラムが完成しました。
system/controlDictからプログラムをincludeするようにします。
|
1 2 3 4 5 |
functions { // #includeFunc solverInfo; //コメントアウト #include "mixedmeantemp" //追加 } |
system/mixedmeantemp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
mixedmeantemp { type coded; libs (utilityFunctionObjects); name mixedmeantemp; codeExecute #{ Info << "========= T_m(z) calculation ===========" << endl; const volVectorField& C = mesh().C(); const scalarField& V = mesh().V(); const volVectorField& U = mesh().lookupObject<volVectorField>("U"); const volScalarField& T = mesh().lookupObject<volScalarField>("T"); const volScalarField& rho = mesh().lookupObject<volScalarField>("rho"); // thermoライブラリから物性値を取得(型推論を使用) // Cp を thermophysicalProperties 辞書から取得 IOdictionary thermoDict ( IOobject ( "thermophysicalProperties", mesh().time().constant(), mesh(), IOobject::MUST_READ_IF_MODIFIED, IOobject::NO_WRITE ) ); const dictionary& mixture = thermoDict.subDict("mixture"); const dictionary& thermoSub = mixture.subDict("thermodynamics"); scalar Cp = readScalar(thermoSub.lookup("Cp")); Info << "Cp from dictionary: " << Cp << endl; scalar radius = 0.02; // 円管の半径 [m] scalar zMin = 0.00; scalar zMax = 1.8; scalar dz = 0.001; // 出力ファイル設定 fileName outputDir = mesh().time().path() / fileName("postProcessing") / fileName("mixedmeantemp") / mesh().time().timeName(); mkDir(outputDir); OFstream outputFile(outputDir/"mixedmeantemp.dat"); outputFile << "# z [m]\tTm(z) [K]" << endl; for (scalar z = zMin; z <= zMax; z += dz) { scalar num_ = 0.0; scalar den_ = 0.0; label count = 0; forAll(C, i) { scalar x = C[i].x(); scalar y = C[i].y(); scalar zc = C[i].z(); if (zc >= z && zc < z + dz) { scalar r = sqrt(x*x + y*y); if (r <= radius) { scalar uz = U[i].z(); scalar temp = T[i]; scalar dens = rho[i]; scalar vol = V[i]; num_ += dens * Cp * uz * temp * vol; den_ += dens * Cp * uz * vol; count++; } } } if (den_ > VSMALL) { scalar Tm = num_ / den_; outputFile << z + dz/2 << "\t" << Tm << endl; } } Info << "Finished writing T_m(z) to: " << outputDir/"mixedmeantemp.dat" << endl; #}; } |
結果を出力するには以下のようにします。
|
1 |
buoyantSimpleFoam -postProcess -latestTime |
※postProcess -func mixedmeantemperature -latestTimeで行おうとしましたが、流速などの物理情報を取得できなかったのでcontrolDictに記載してfunction objectsとして出力しています。
このプログラムによりpostProcessing/mixedmeantemperature/1000/mixedmeantemp.datに以下のデータが出力されます。
こちらは混合平均温度は$T_m = \frac{ \int_0^{R} \rho C_p u(r) T \, 2\pi r\,dr}{ \int_0^R \rho C_p u(r) \, 2\pi r\,dr}$をOpenFOAMのデータから出力したものになります。
理論計算式と比較
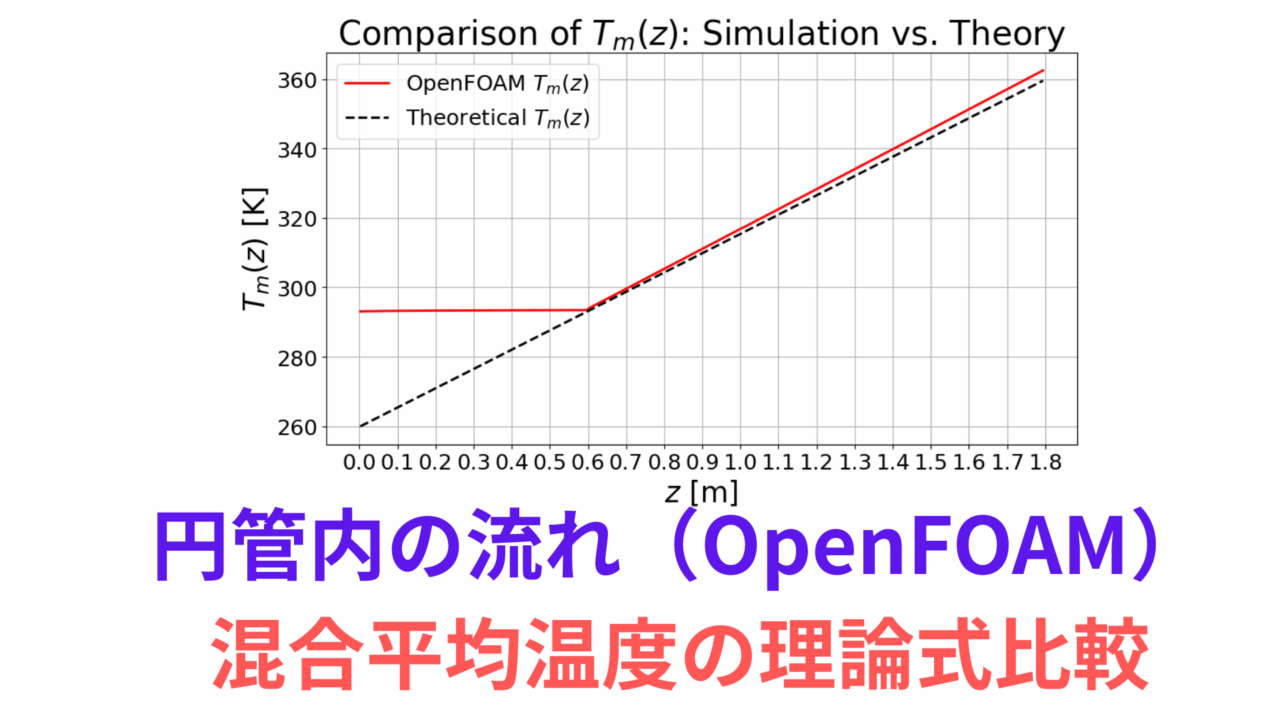
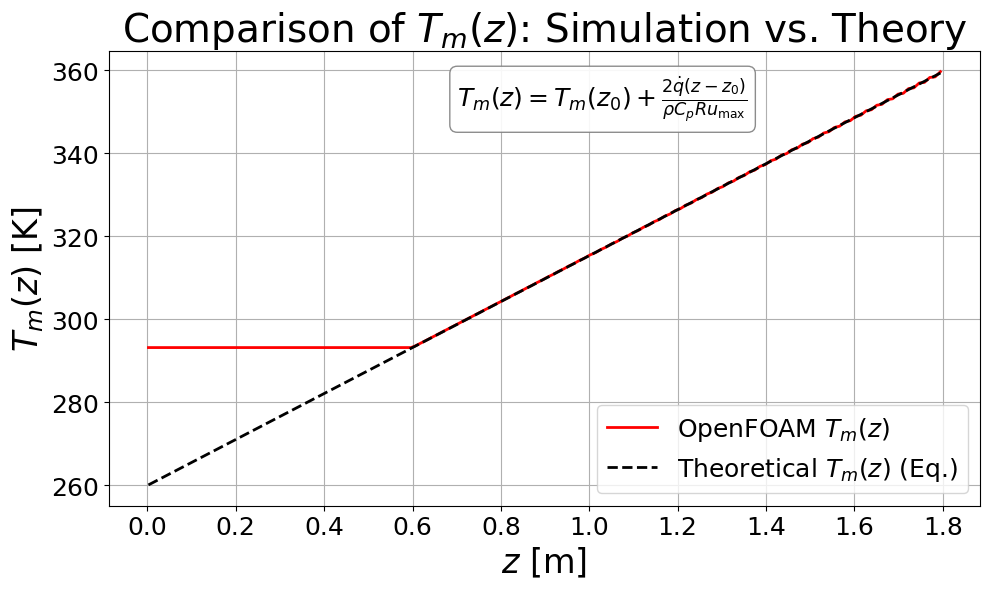
では、先ほど出力した混合平均温度$T_m(z)$と理論式の$T_m(z)=T_m(z_0)+\frac{2\dot{q}(z-z_0)}{\rho C_p R u_{\mathrm{max}}}$と比較することにします。
Pythonで以下のようにプログラムを作成し比較します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np import matplotlib.pyplot as plt # データ読み込み data = np.loadtxt("postProcessing/mixedmeantemperature/1000/mixedmeantemperature.dat", comments="#") z = data[:, 0] Tm = data[:, 1] # 定数(理論式) T0 = 293.15 # 初期温度 [K] Cp = 1000 # 比熱 [J/kg/K] R = 0.01 # 半径 [m] umax = 0.3 # 最大速度 [m/s] rho = 1.2 # 密度 [kg/m3] qdot = 100 # 熱流束 [W/m2] z0 = 0.6 # 基準位置 # 理論解 Tm_theory = T0 + (2 * qdot * (z - z0)) / (rho * Cp * R * umax) # プロット fig, ax = plt.subplots(figsize=(10, 6)) ax.plot(z, Tm, label=r"OpenFOAM $T_m(z)$", color="red", linewidth=2) ax.plot(z, Tm_theory, label=r"Theoretical $T_m(z)$", color="black", linestyle="--", linewidth=2) # 軸ラベル・タイトル ax.set_xlabel(r"$z$ [m]", fontsize=24) ax.set_ylabel(r"$T_m(z)$ [K]", fontsize=24) ax.set_title(r"Comparison of $T_m(z)$: Simulation vs. Theory", fontsize=28) # 軸目盛フォント ax.tick_params(axis='both', which='major', labelsize=18) # 凡例・グリッド・保存 ax.grid(True) ax.legend(fontsize=18) fig.tight_layout() fig.savefig("Tm_comparison.pdf", format="pdf") plt.show() |
結果は以下となります。
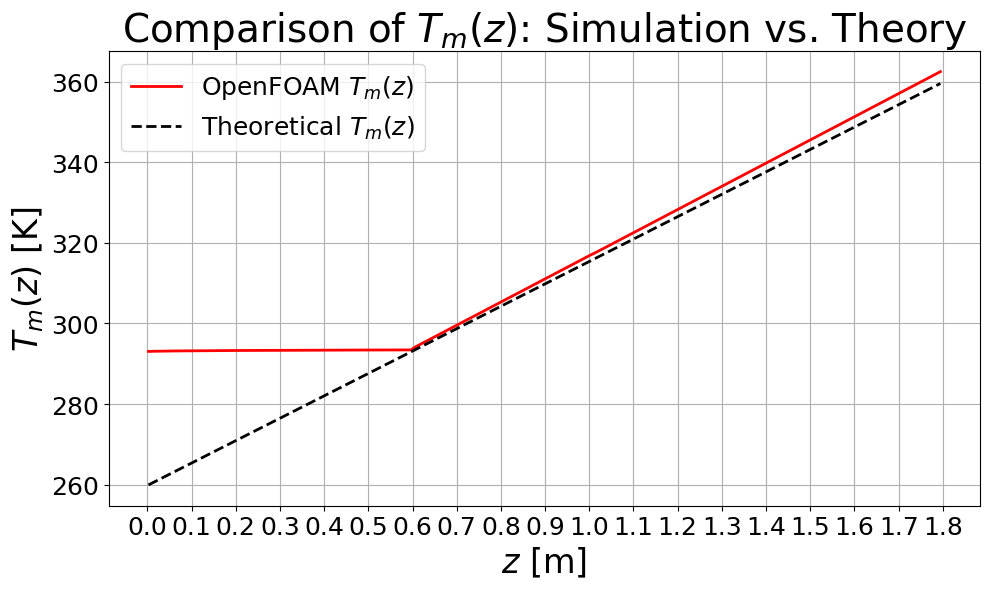
$z_0=0.6$までが助走区間としているので、$z_0\geq 0.6$を見るとほぼ理論式通りになっていることが確認できます。
2000ステップまで計算させるともう少し良い一致が確認できます。
まとめ
今回は、OpenFOAMを用いた円管内の熱流体解析において、混合平均温度 $T_m(z)$ を求める方法を紹介しました。
-
混合平均温度は、エネルギー輸送の観点から定義される重要な量であり、解析結果の物理的妥当性を評価する指標にもなります。
-
OpenFOAM標準では $T_m(z)$ を直接出力できないため、
codedFunctionObjectを用いて独自に出力プログラムを作成しました。 -
出力された温度分布は、理論解$T_m(z)=T_m(z_0)+\frac{2\dot{q}(z-z_0)}{\rho C_p R u_{\mathrm{max}}}$と非常によく一致しており、数値解析の信頼性を確認できました。
技術書典18では、本記事の「2次元円柱まわりの熱流体解析」やそのほかの熱流体のテーマを取り扱う予定です。
次回の技術書典18に向けて内容を考え中です。
乞うご期待!!
計算力学技術者のための問題アプリ
計算力学技術者熱流体2級、1級対策アプリをリリースしました。
- 下記をクリックしてホームページでダウンロードできます。
- LINE公式に登録すると無料で問題の一部を閲覧できます。
※LINEの仕様で数式がずれていますが、アプリでは問題ありません。
- 計算力学技術者の熱流体2級問題アプリ作成
リリース後も試行錯誤をしながら改善に努め日々アップデートしています。
備忘録として作成の過程を綴っています。
OpenFOAMに関する技術書を販売中!
OpenFOAMを自宅で学べるシリーズを販売中です。
OpenFOAM初学者から中級者向けの技術書となっていますので、ぜひよろしくお願いいたします。
お勧めの参考書
本記事の内容について触れている書籍がこちらです。
CFD(流体解析)のガイドブックというタイトルだけあって、熱流体に関する内容は網羅的に書かれています。
乱流モデルの数式の展開が非常に丁寧なのはこちらの参考書です。
今まで読んだ本の中で途中式もしっかり書いてあって一番丁寧でした。
乱流モデルの話だけでなく、混相流(気液、固液)や粒子法、浅水方程式の話も乗っているので重宝しています。
乱流モデルはこちらもお勧めです。
前半は数値シミュレーションの離散化の話で、後半に乱流モデルの話が出てきます。
乱流モデルのざっくりした解説と流体全般の基礎知識にはこちらがちょうど良いでしょう。