こんにちは(@t_kun_kamakiri)
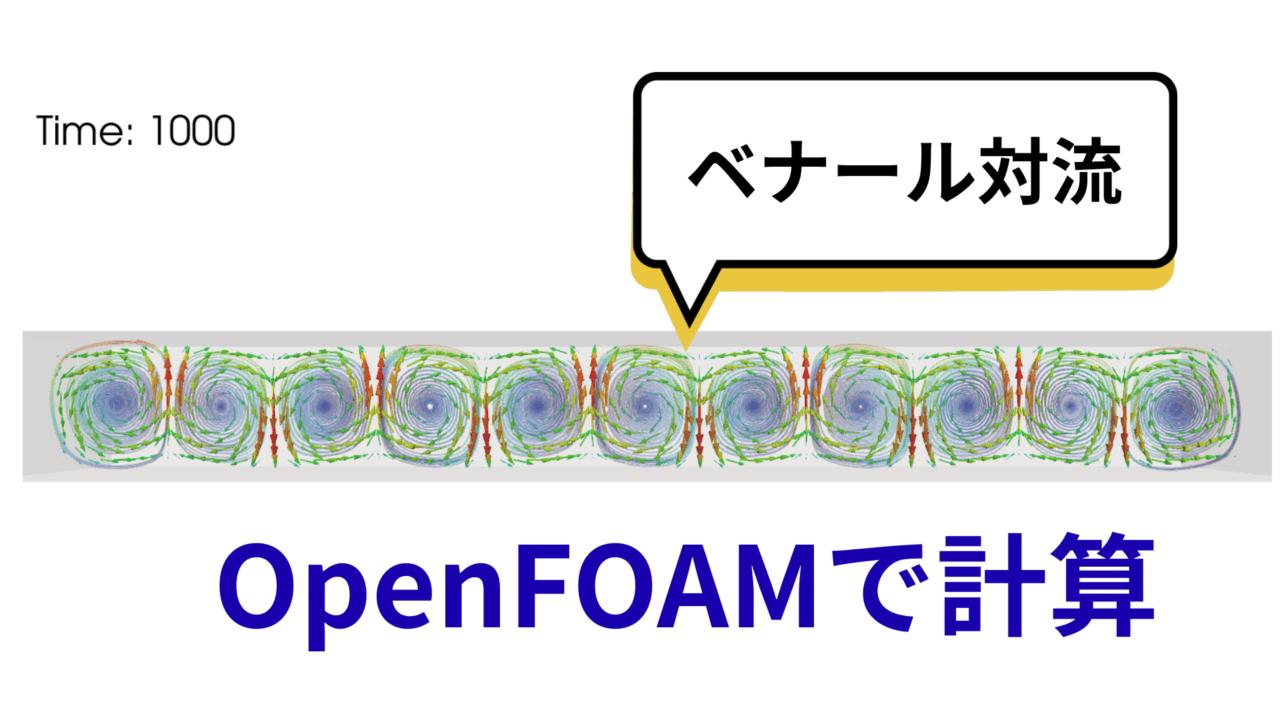
ベナール対流は、液体の底面を温めたときに自然に生まれる「六角形のセル模様」が特徴的な対流現象です。

下から加熱されて軽くなった流体が上昇し、冷えて重くなった流体が下降することで、規則的な渦のパターンが自発的に形成されます。
外から“回せ”と指示しなくても、温度差だけで秩序ある流れが生まれる点が非常に興味深い現象です。
本記事では、この ベナール対流を OpenFOAM を用いて数値的に再現し、温度分布やセル構造がどのように形成されるのかを確認していきます。
OpenFOAMのチュートリアルにあるベナール対流を計算してみよう
熱対流の基礎を学ぶ上でも、自然対流モデルの検証ケースとしても、非常に分かりやすい題材です。
また、チュートリアルを実行するだけですのでOpenFOAMをインストールされている方であれば、すぐに試すことができます。
こういった可視化すると楽しい現象を見つけて、OpenFOAMを学ぶのもモチベーションを保つコツです。
OpenFOAM v2412(WSL2 Ubuntu-24.04)
チュートリアルのコピー
チュートリアルをコピーします。
|
1 |
cp -r $FOAM_TUTORIALS/heatTransfer/buoyantBoussinesqPimpleFoam/BenardCells . |
$FOAM_TUTORIALS = /usr/lib/openfoam/openfoam2412/tutorials
という変数ですので、ご自身使用している環境に合ったバージョンがはいります。
続いてフォルダを移動します。
|
1 |
cd BenardCells |
メッシュ作成
今回は2次元の解析になりますので$z$軸方向は1層のメッシュです。
blockMeshDictを確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
scale 1; vertices ( (0 0 -1) (9 0 -1) (9 1 -1) (0 1 -1) (0 0 1) (9 0 1) (9 1 1) (0 1 1) ); blocks ( hex (0 1 2 3 4 5 6 7) (90 10 1) simpleGrading (1 1 1) ); edges ( ); boundary ( floor { type wall; faces ( (1 5 4 0) ); } ceiling { type wall; faces ( (3 7 6 2) ); } sideWalls { type wall; faces ( (0 4 7 3) (2 6 5 1) ); } frontAndBack { type empty; faces ( (0 3 2 1) (4 5 6 7) ); } ); mergePatchPairs ( ); |
以下のコマンドでメッシュを作成します。
|
1 |
blockMesh |
ParaViewで確認するためには空ファイルを用意します。
|
1 |
touch post.foam |
blockMeshDictで設定した境界面の名前が作成されています。
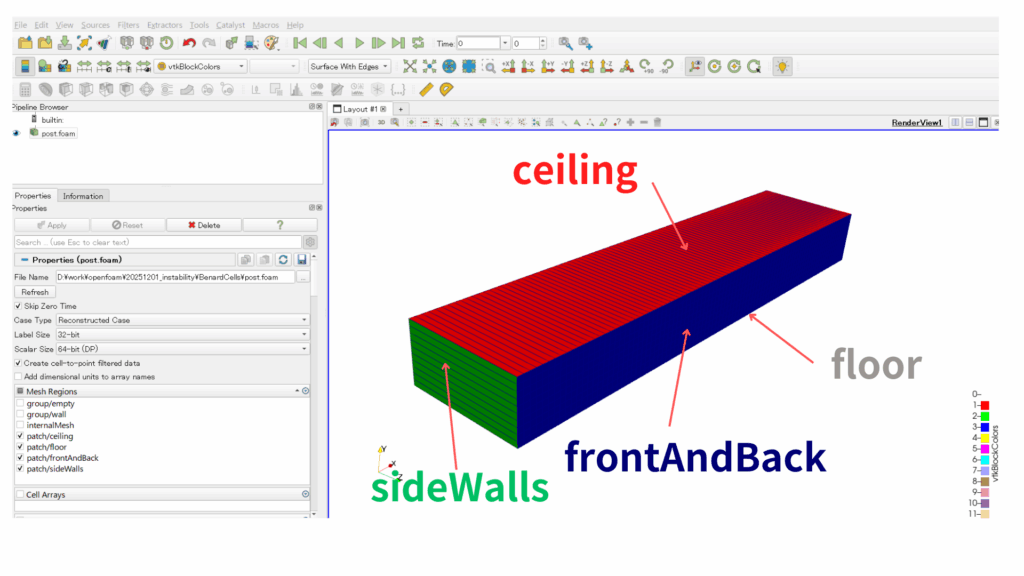
境界条件
チュートリアルのままですが境界条件を載せておきます。
0/U
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
dimensions [0 1 -1 0 0 0 0]; internalField uniform (1e-4 0 0); boundaryField { wall { type noSlip; } #includeEtc "caseDicts/setConstraintTypes" } |
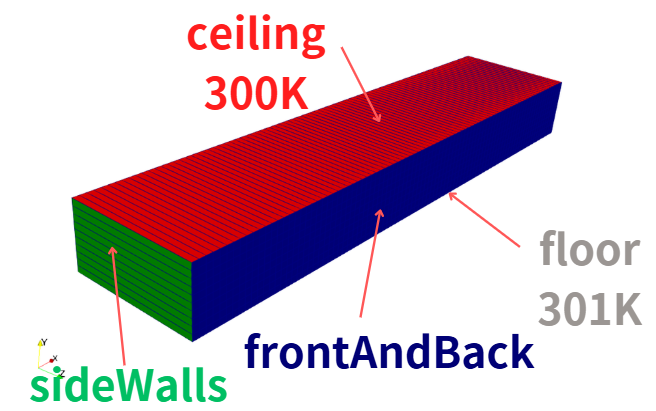
0/T
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
dimensions [0 0 0 1 0 0 0]; internalField uniform 300; boundaryField { floor { type fixedValue; value uniform 301; } ceiling { type fixedValue; value uniform 300; } sideWalls { type zeroGradient; } #includeEtc "caseDicts/setConstraintTypes" } |
0/p_rgh
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { wall { type fixedFluxPressure; rho rhok; value $internalField; } #includeEtc "caseDicts/setConstraintTypes" } |
0/p
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
dimensions [0 2 -2 0 0 0 0]; internalField uniform 0; boundaryField { wall { type calculated; value $internalField; } #includeEtc "caseDicts/setConstraintTypes" } |
0/k
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
dimensions [0 2 -2 0 0 0 0]; internalField uniform 1e-5; boundaryField { wall { type kqRWallFunction; value $internalField; } #includeEtc "caseDicts/setConstraintTypes" } |
0/epsilon
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
dimensions [0 2 -3 0 0 0 0]; internalField uniform 1e-5; boundaryField { wall { type epsilonWallFunction; value $internalField; } #includeEtc "caseDicts/setConstraintTypes" } |
0/alphat
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
dimensions [0 2 -1 0 0 0 0]; internalField uniform 0; boundaryField { wall { type alphatJayatillekeWallFunction; Prt 0.85; value $internalField; } #includeEtc "caseDicts/setConstraintTypes" } |
離散化スキームと代数ソルバ
離散化スキームはいろいろありますが、余裕があればこちらもお読みください。

system/fvSchemes
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
ddtSchemes { default Euler; } gradSchemes { default Gauss linear; } divSchemes { default none; div(phi,U) Gauss linearUpwind grad(U); div(phi,T) Gauss limitedLinear 1; turbulence Gauss limitedLinear 1; div(phi,k) $turbulence; div(phi,epsilon) $turbulence; div((nuEff*dev2(T(grad(U))))) Gauss linear; } laplacianSchemes { default Gauss linear corrected; } interpolationSchemes { default linear; } snGradSchemes { default corrected; } |
代数ソルバはこちらをごさんこうください。
system/fvSolution
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
solvers { p_rgh { solver GAMG; smoother DIC; tolerance 1e-8; relTol 0.01; } p_rghFinal { $p_rgh; relTol 0; } "(U|T|k|epsilon)" { solver PBiCGStab; preconditioner DILU; tolerance 1e-8; relTol 0.01; } "(U|T|k|epsilon)Final" { $T; relTol 0; } } PIMPLE { momentumPredictor no; nNonOrthogonalCorrectors 0; nCorrectors 2; pRefCell 0; pRefValue 0; } relaxationFactors { equations { ".*" 1.0; } } |
計算制御の設定
system/controlDict
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
application buoyantBoussinesqPimpleFoam; startFrom latestTime; startTime 0; stopAt endTime; endTime 1000; deltaT 1; writeControl runTime; writeInterval 50; purgeWrite 0; writeFormat binary; writePrecision 6; writeCompression off; timeFormat general; timePrecision 6; runTimeModifiable true; functions { #includeFunc solverInfo #includeFunc streamlines } |
functionsの中に2つ設定ファイルがあります。
1つ目が残差を出力する設定ファイルです。
ここでは圧力(p_rgh)の残差のみを出力しています。
|
1 2 3 4 5 6 7 |
#includeEtc "caseDicts/postProcessing/numerical/solverInfo.cfg" writeControl writeTime; fields (p_rgh); writeFields yes; |
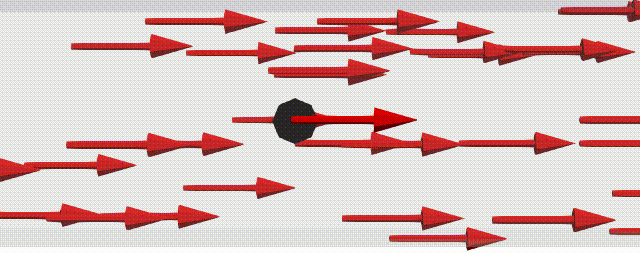
2つ目が流線のvtkファイルを出力する設定ファイルです。
こちらの設定によりstartからendの直線を通過するstreamlines(流線)を作ります。
|
1 2 3 4 5 6 |
nLines 24; start (0 0.5 0); end (9 0.5 0); fields (p); #includeEtc "caseDicts/postProcessing/visualization/streamlines.cfg" |
このように必要に応じて出力する設定ファイルを各自用意することになります。
設定ファイルはネットから調べてくる必要がありますが、とりあえずはチュートリアルのままで良いでしょう。
では、計算を実行します。
|
1 |
buoyantBoussinesqPimpleFoam |
計算は1分くらいで終わると思います。
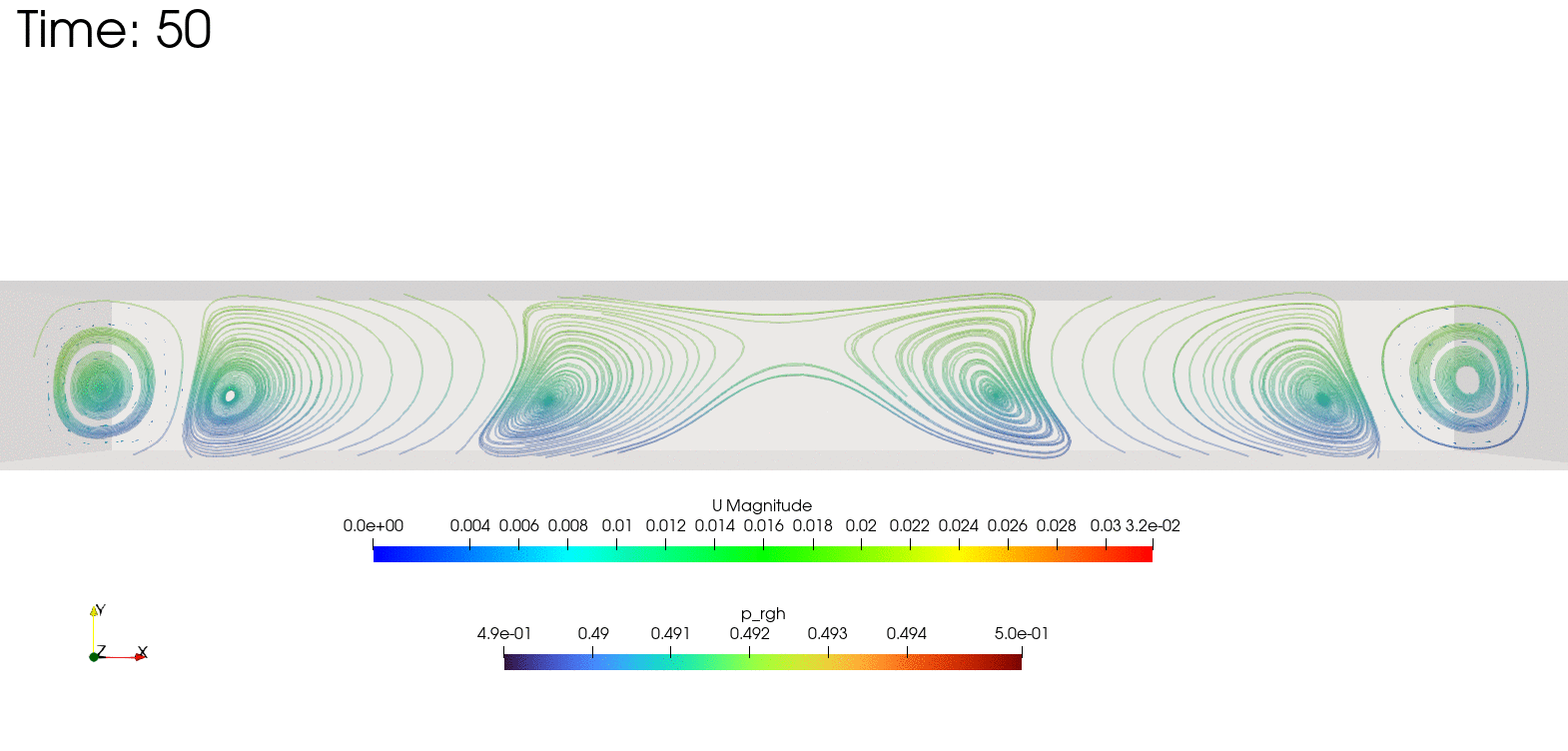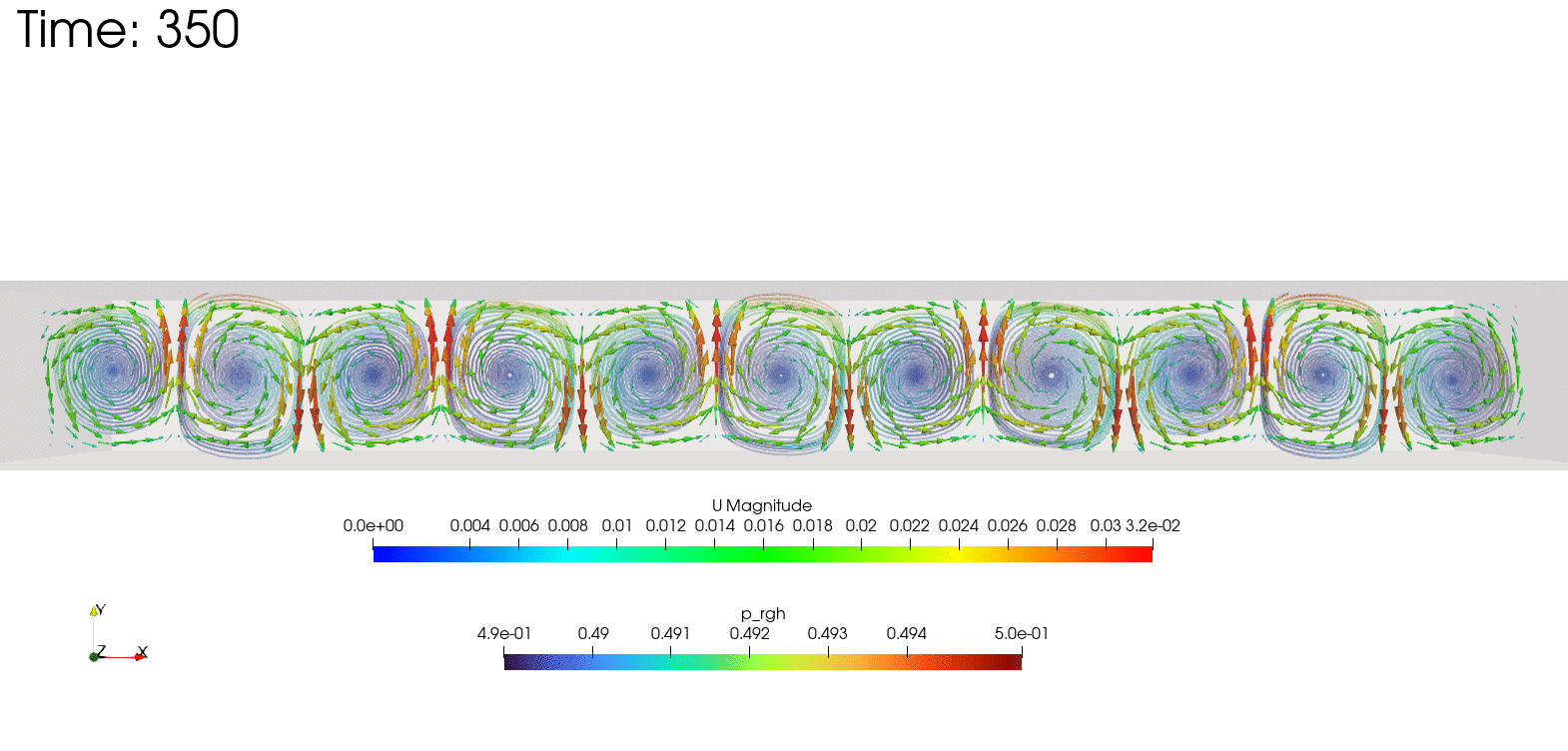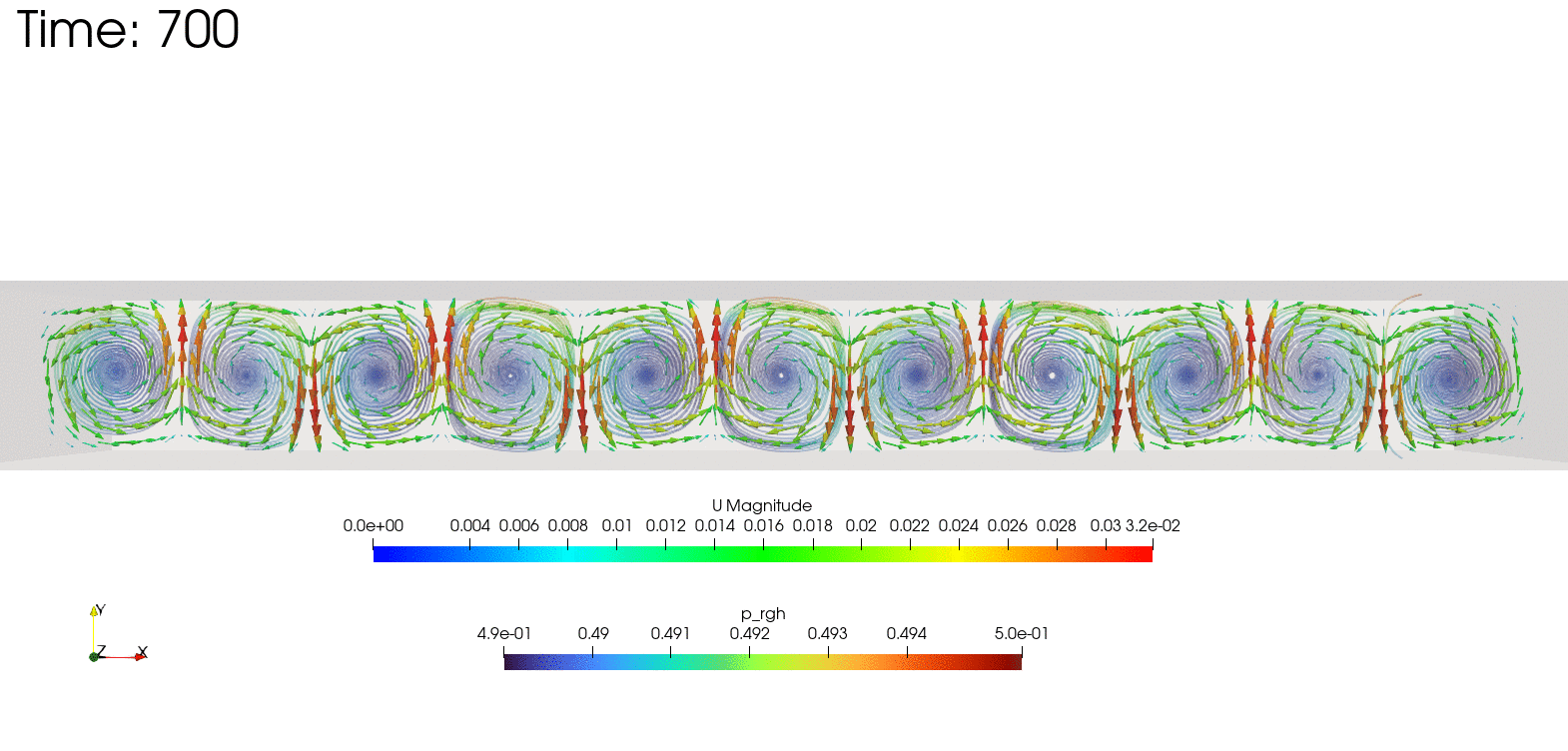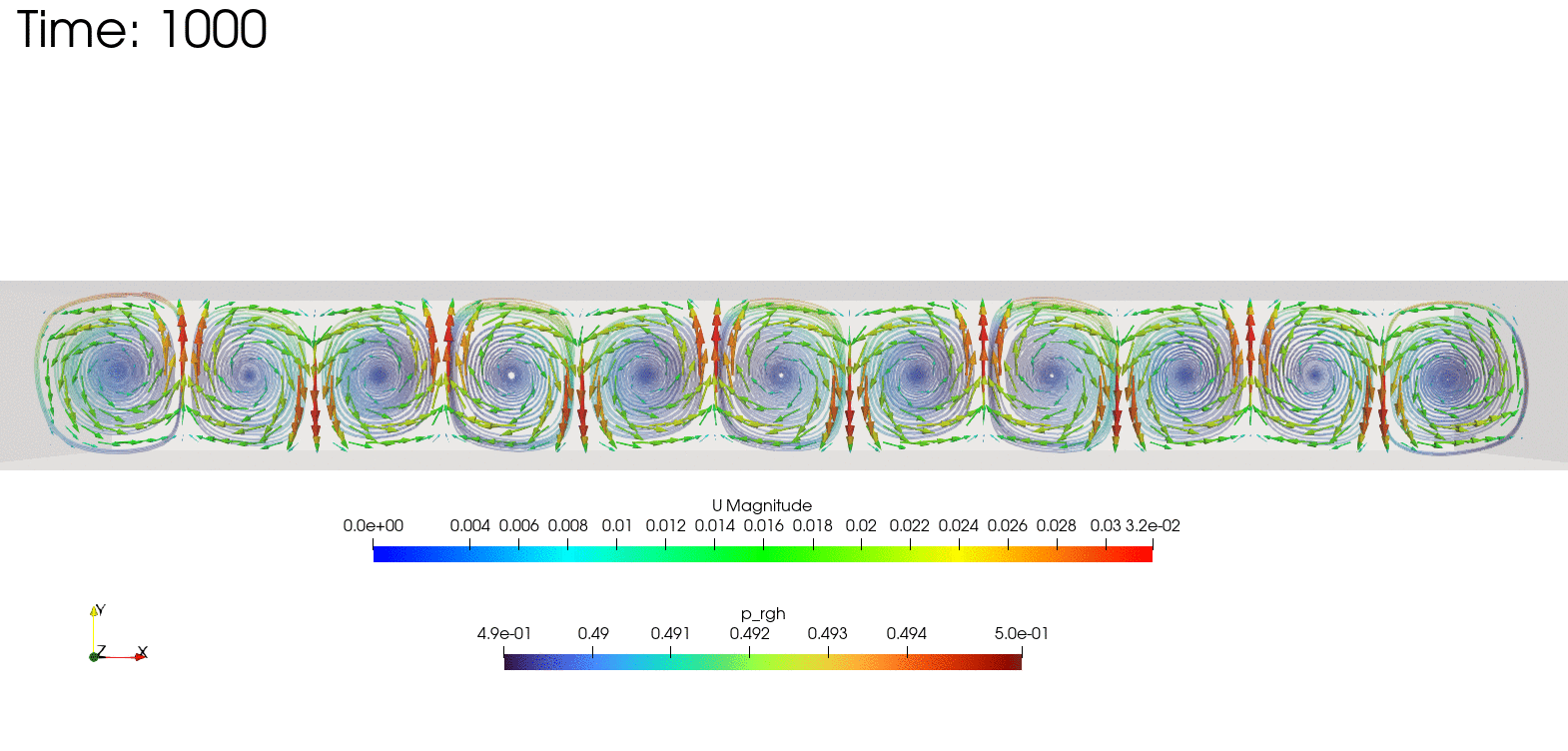
結果の確認
postProcessing/sets/streamlines/1000/track0.vtp
をParaViewで読み込むと