こんにちは(@t_kun_kamakiri)
まず流体解析の魅力のひとつはカラフルで美しい可視化ができる点にあると考えています。 CFDはComputational Fluid Dynamicsの略で意味は数値流体力学ではあるが、一瞬Colorful Fluid Dynamicsの意味だったかなと思えるほど美しいときがあります。
それゆえに、いろいろな意味ではまることが多いのが流体解析である。
流体の美しい(不安定な)現象を紹介する
本記事ではそんな流体力学の美しい不安定性現象を集めてみました。
※厳密には不安定性現象として名前がついていないものもありますが、流体現象として美しいと思うのを集めたという趣旨でご理解ください。
ケルビン・ヘルムホルツ不安定性
ケルビン・ヘルムホルツ不安定性(Kelvin–Helmholtz instability)とは、異なる速度(密度)をもつ2相の間で起こる不安定性現象です。
2相の界面でせん断力があるため不安定性の種(渦)が生じ、それが時間とともに増幅することで生じる2次元的な模様のことを指します。
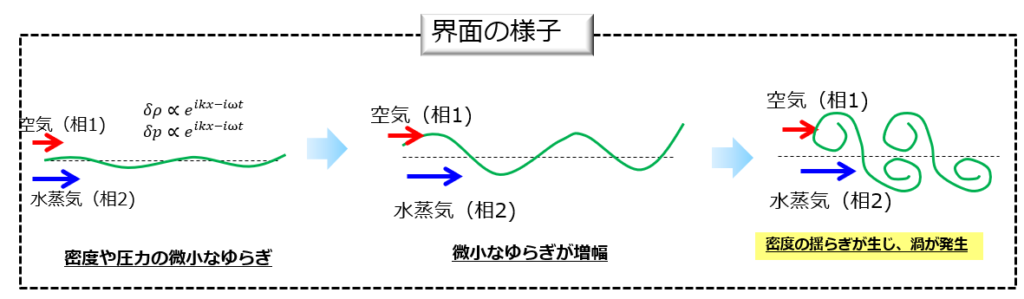
日常で見かけるものとしては、飛行機の窓から外を眺めているとたまに見かける渦を巻いた雲。

それから、木星の縞模様も、流体力学の不安定性が生み出した風景のひとつです。

こちらをOpenFOAMで2次元計算させたものを載せておきます。
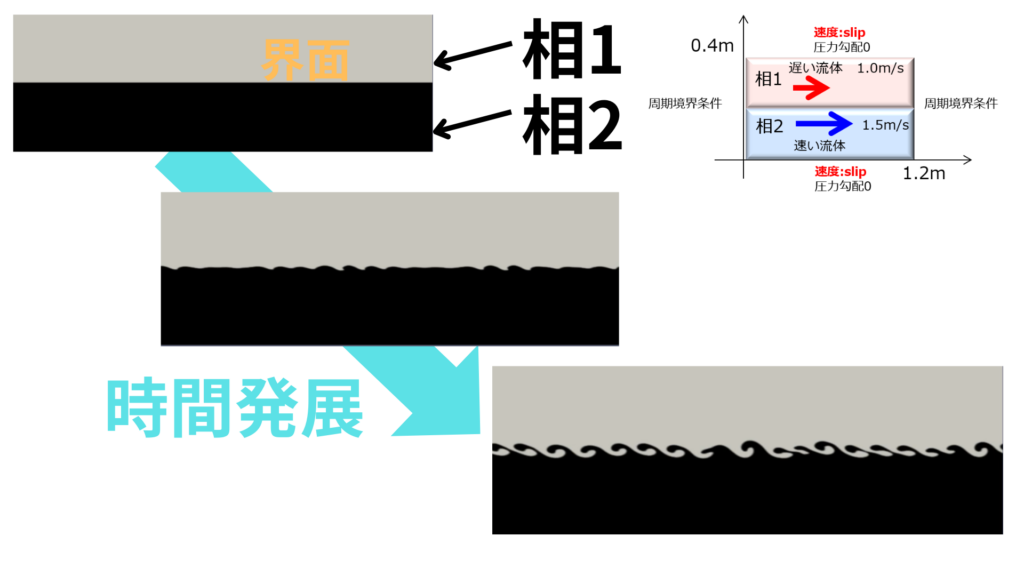

レイリー・テイラー不安定性
レイリー・テーラー不安定性(Rayleigh–Taylor instability)とは、重い流体が軽い流体の上にあるという「不安定な配置」で、わずかな擾乱(ゆらぎ)をきっかけに、界面が崩れて混ざり合っていく現象です。
コップの中で
- 上:重い液体
- 下:軽い液体
という状態を無理やり作ると、重い流体は「下に落ちたい」、軽い流体は「上に上がりたい」。この重力に逆らった配置そのものが不安定で、境界面に小さな凹凸ができた瞬間から、フィンガー状・キノコ状が成長していきます。
こちらをOpenFOAMで2次元計算させたものを載せておきます。
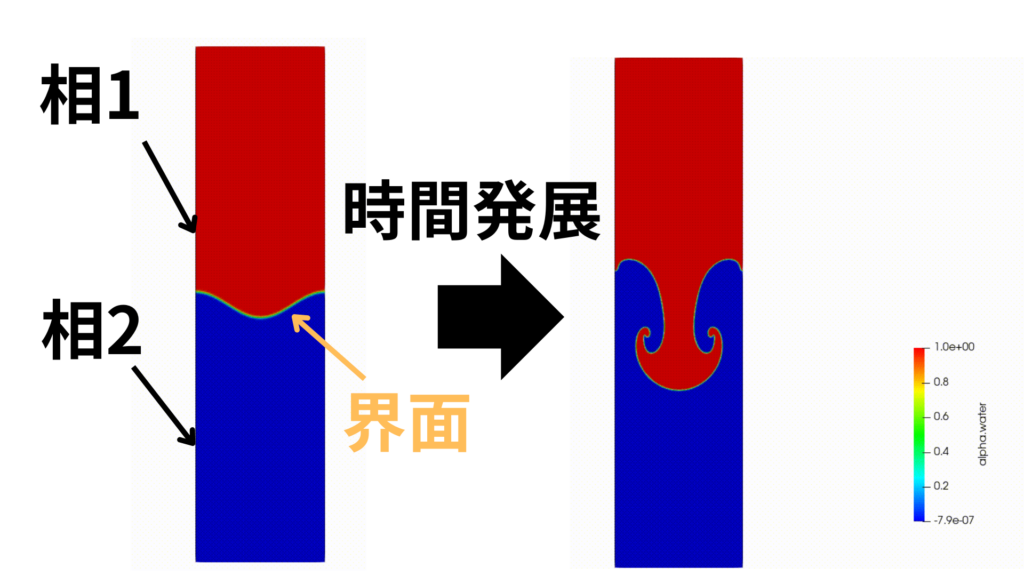
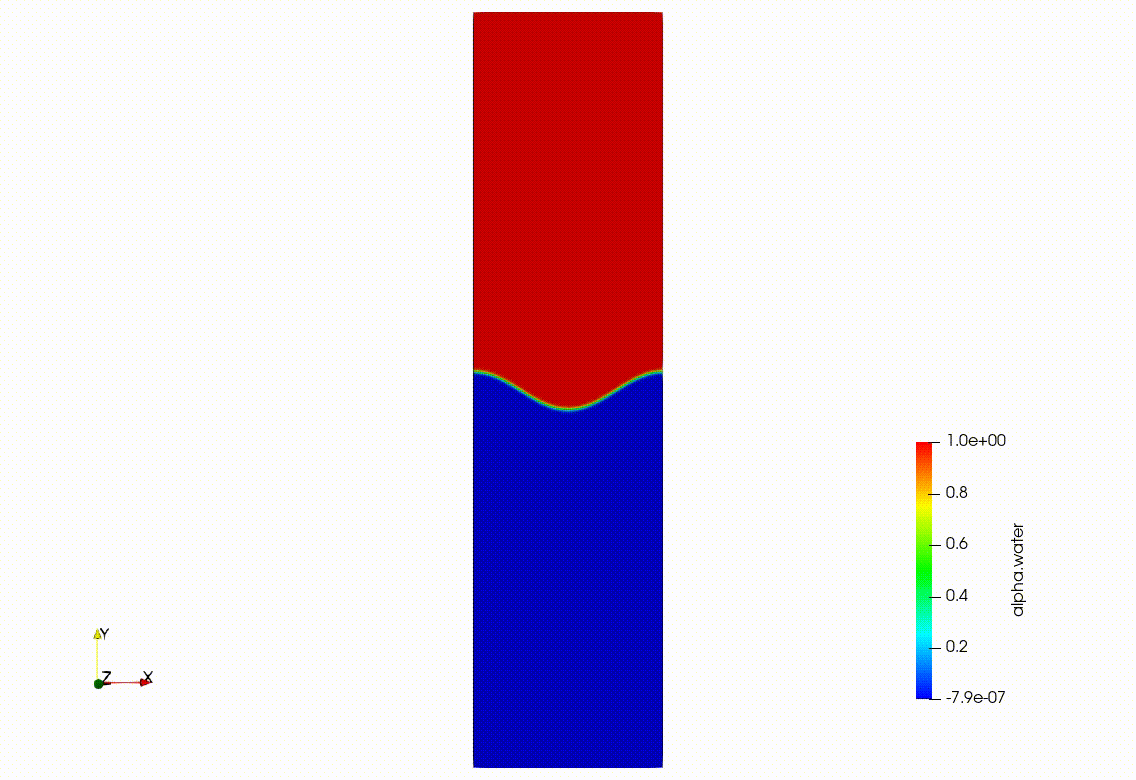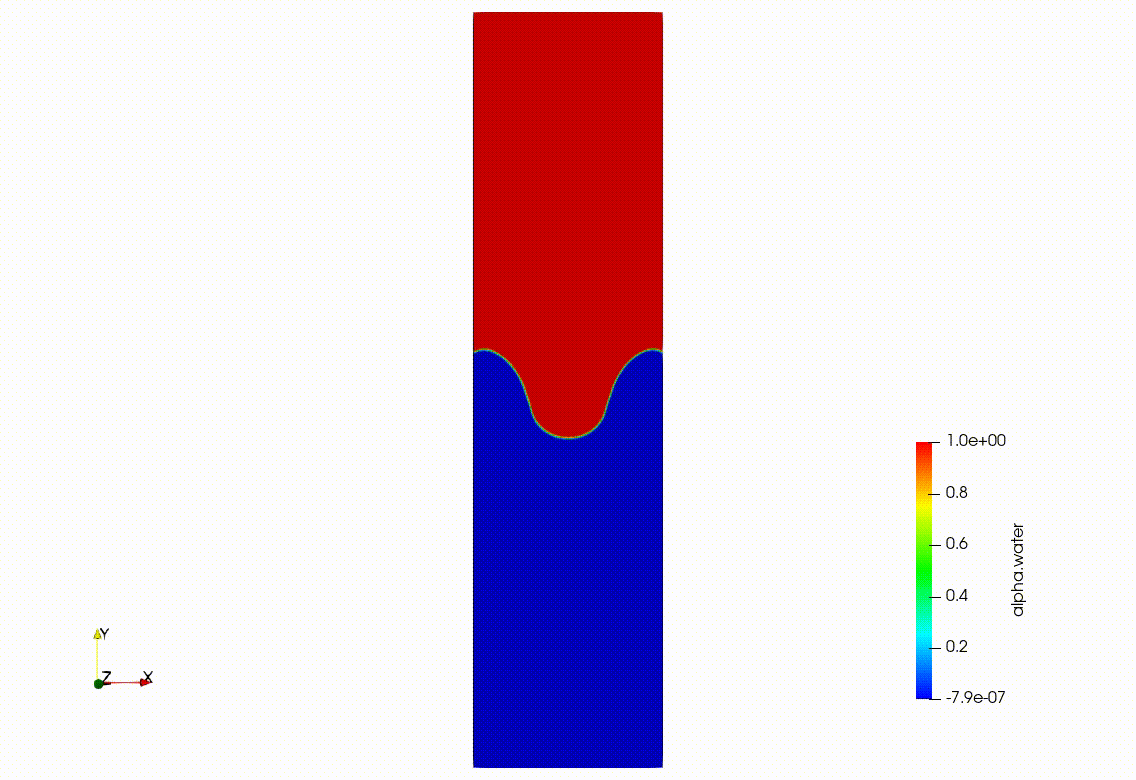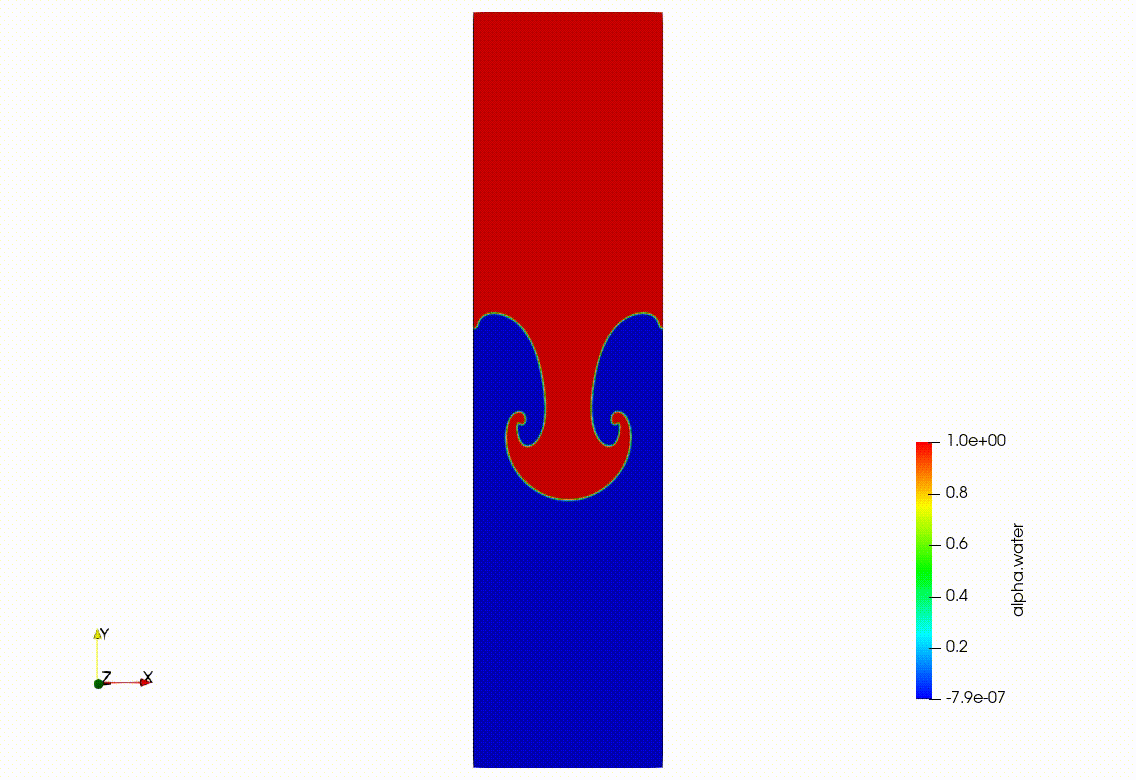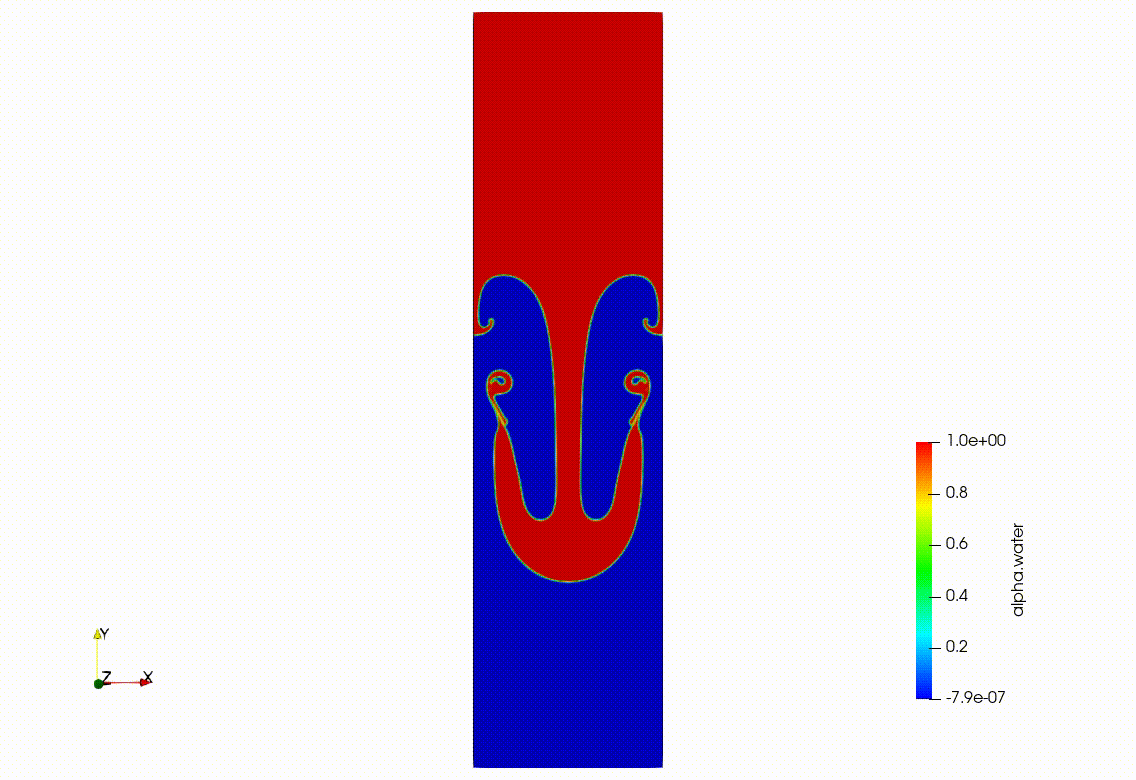
ケルビンヘルムホルツ不安定性、レイリーテイラー不安定性に関して線形理論から丁寧に解説した記事がこちらです。
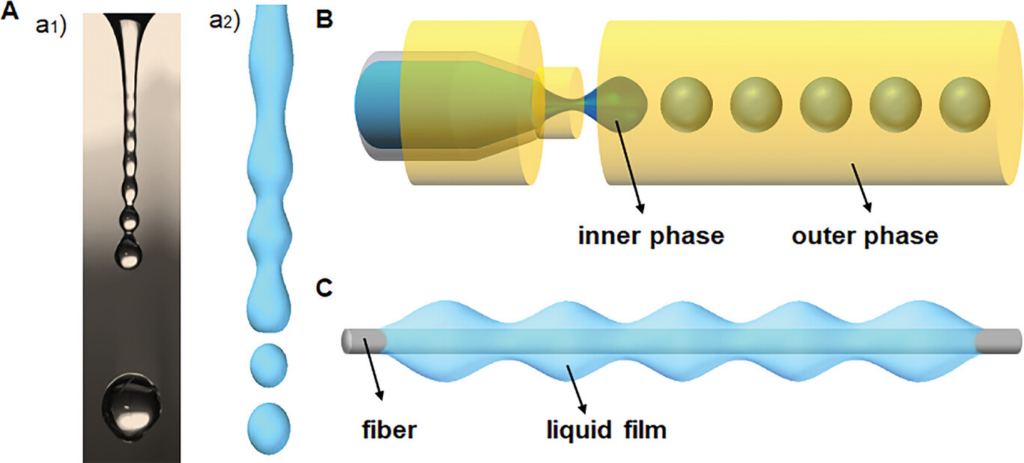
プラトー・レイリー不安定性
プラトー・レイリー不安定性とは、細長い液体の柱や液体ジェットが、表面張力の作用でくびれ、最終的に液滴へと分裂してしまう現象です。
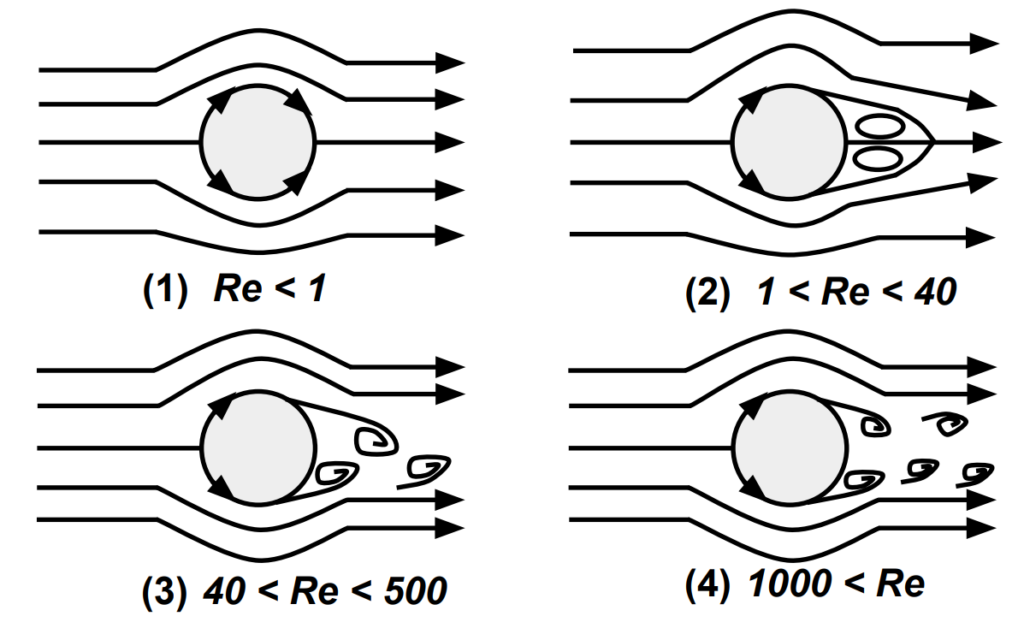
カルマン渦列
(1) レイノルズ数が 1 程度またはそれ以下の場合は、流れは上下対称の定常層流で
あり、円柱背後には渦は発生しない。
(2) レイノルズ数が約 40 程度の場合は、流れは上下対称の定常層流であるが、円
柱背後に上下対称の双子の渦が発生する。
(3) レイノルズ数が 50~500 程度の場合は、流れの上下の対称性が崩れて円柱背後
の渦は上下に放出し、後流に周期的に上下に交互に放出されるカルマン渦列を
形成する。
(4) レイノルズ数が 1000 程度以上になると、後流に放出される渦は乱れ、様々な
大きさの渦を含むようになり、乱流の様相を呈してくる。
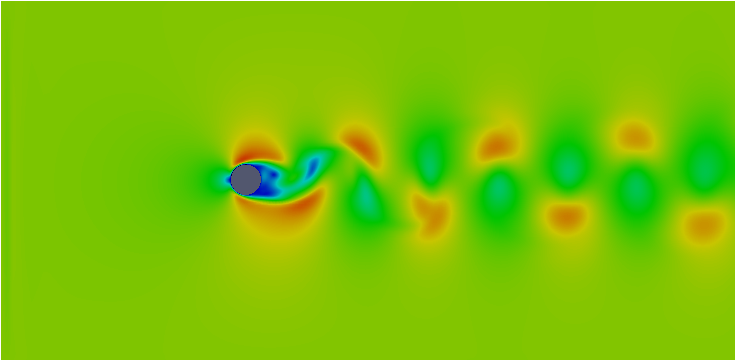
こちらをOpenFOAMで2次元計算させたものを載せておきます。
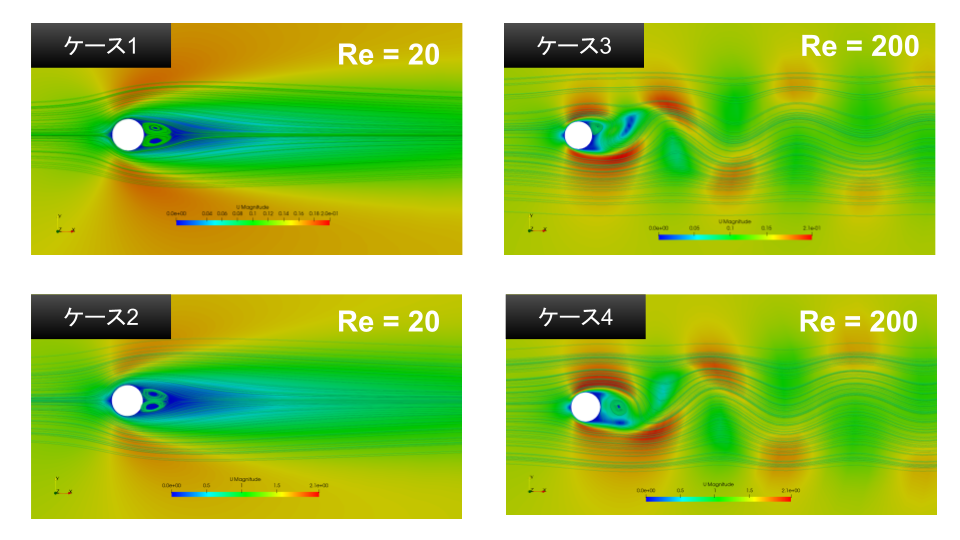
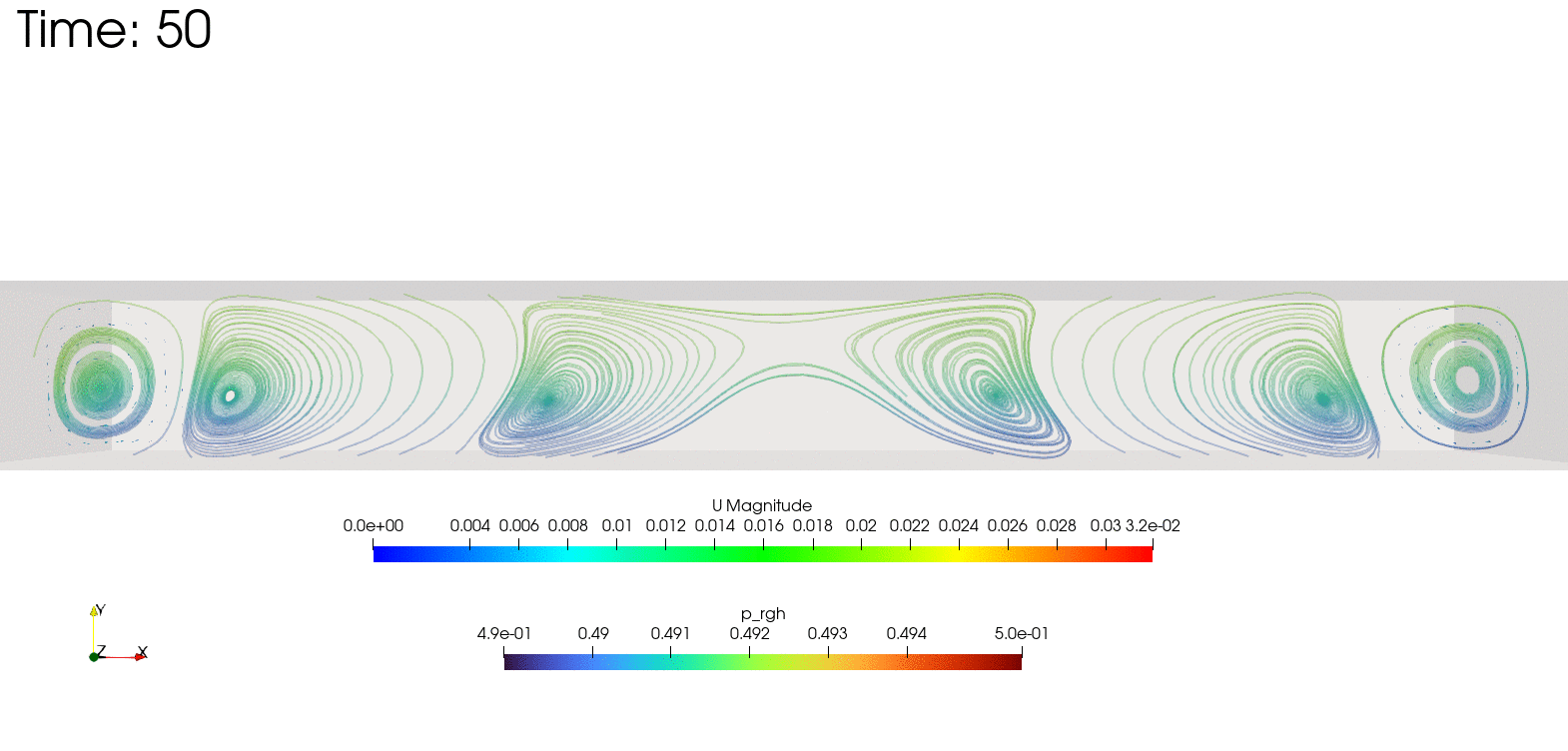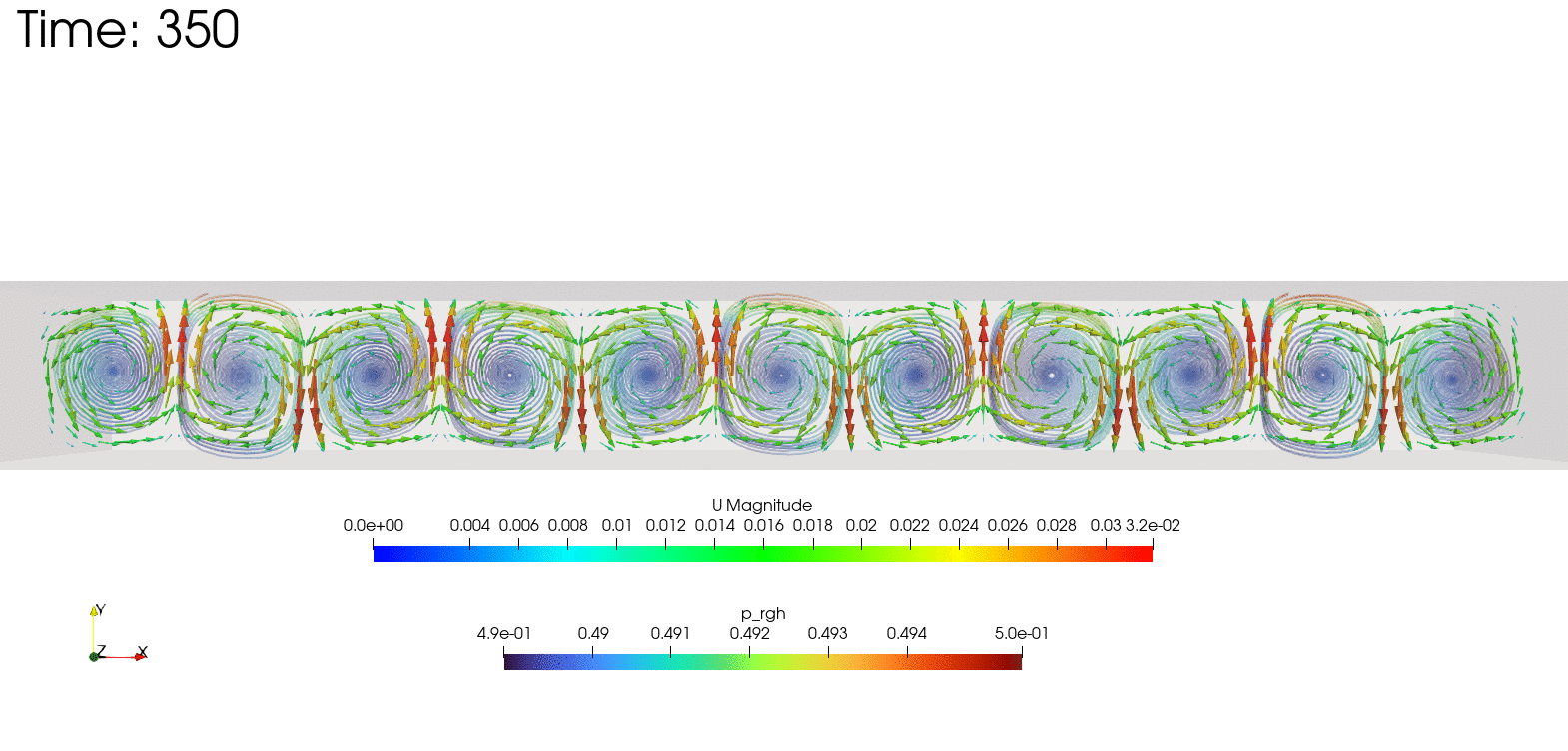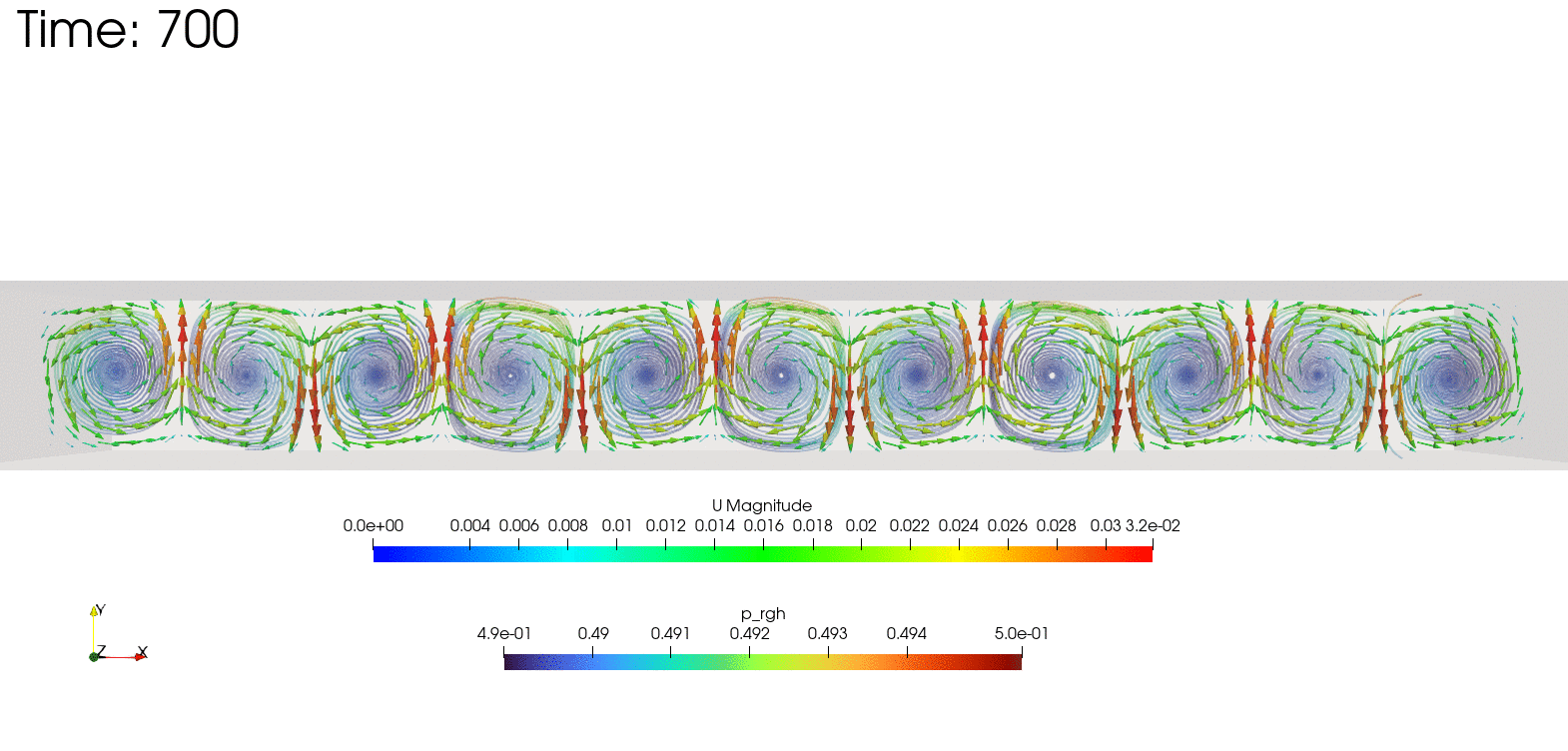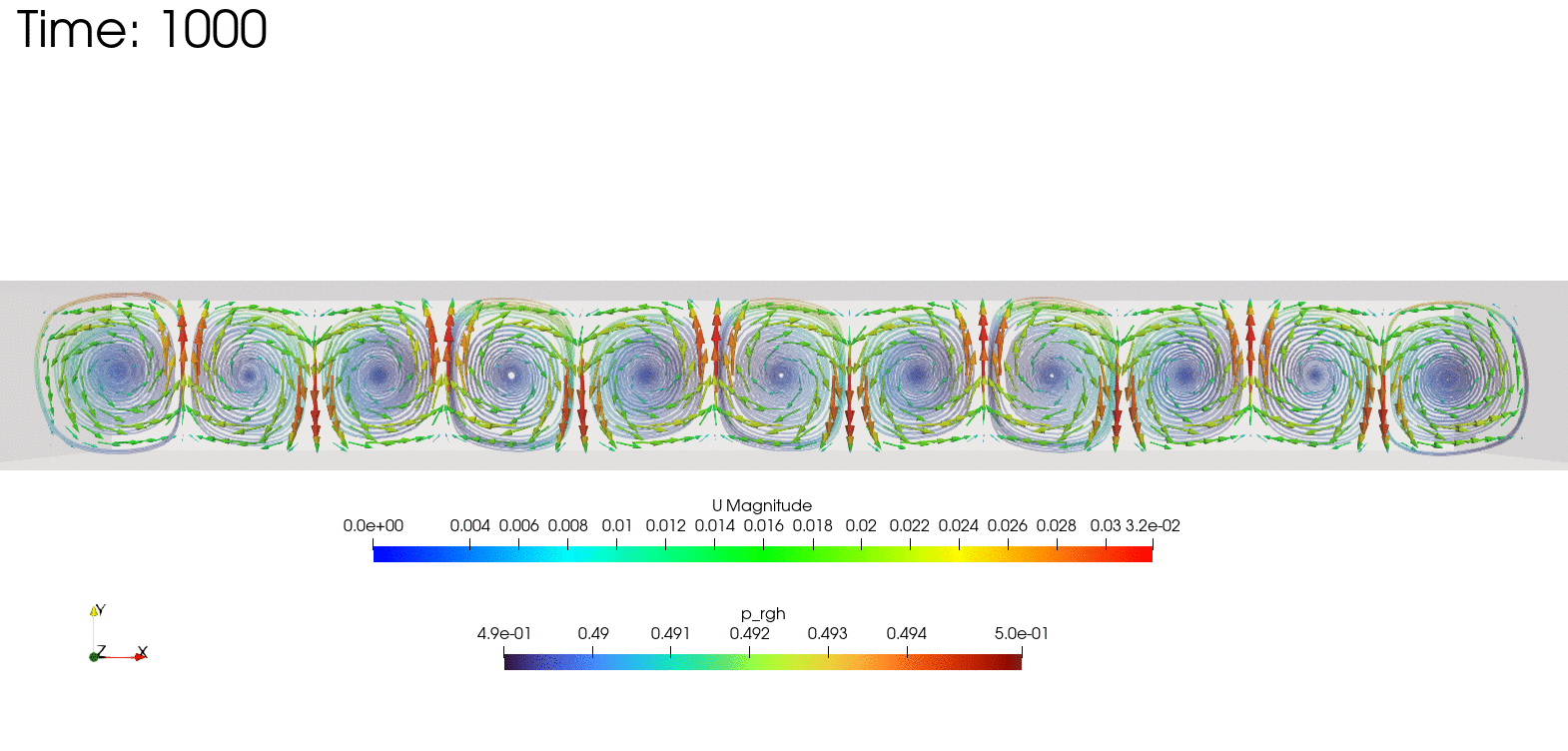
ベナール対流
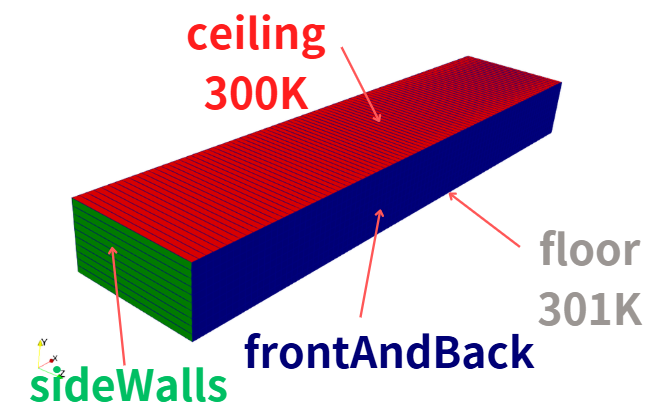
ベナール対流とは、下から温められた流体が、一定条件を超えると自発的に規則正しい対流模様を作る現象です。
こちらをOpenFOAMで2次元計算させたものを載せておきます。
ジーンズ不安定性
ジーンズ不安定性とは、重力によって、ガスや星間物質の雲が自分自身の重さに耐えきれず、収縮を始めてしまう現象です。
宇宙に広がるガスの雲を想像してください。
この雲の中では、
- 外へ広がろうとする力:熱による圧力
- 内へ引き寄せる力:重力
がせめぎ合っています。もし雲が十分に大きく、重く、冷えていると、
熱の力では支えきれなくなり、雲は一気に縮み始めます。
これがジーンズ不安定性です。
こちらは流体現象というよりは、宇宙のお話かもしれませんが、圧縮性の流れとして支配方程式を立てて実現できるかもしれません。
パーカー不安定性
パーカー不安定性とは、重力のある空間で、磁場に支えられたガスが不安定になり、磁力線が波打ってガスが落ち込む現象です。
主に銀河円盤のような、重力・ガス・磁場が共存する環境で起こります。
銀河の中では、ガスは下向きに引かれる重力を受けつつ、磁場(磁力線)にハンモックのように支えられて存在しています。この磁場が少しでも波打つと、
低くなった部分にガスが集まってさらに重くなり、ますます沈み込む——この自己増幅がパーカー不安定性です。
プラントル・グロワートの特異点
飛行機が音速に近い速度(マッハ1付近)で飛ぶと、機体の周りで空気が急激に膨張 → 冷却し、水蒸気が凝結して白い円すい状の雲が現れることがあります。
これが ベイパーコーン です。
このとき、プラントル・グロワート則という亜音速用の近似理論を使うと、「マッハ数が1に近づくほど圧力変化が無限大になる」という計算結果が出てしまいます。
これが プラントル・グロワートの特異点です。
しかし現実では、圧力は無限大にならず、その代わりに急激な圧力変化が可視化された結果としてベイパーコーンが見えるだけ。
つまり特異点とは、現象が爆発的に強くなる境目を、理論が扱えなくなったサイン
だと考えると理解しやすいです。
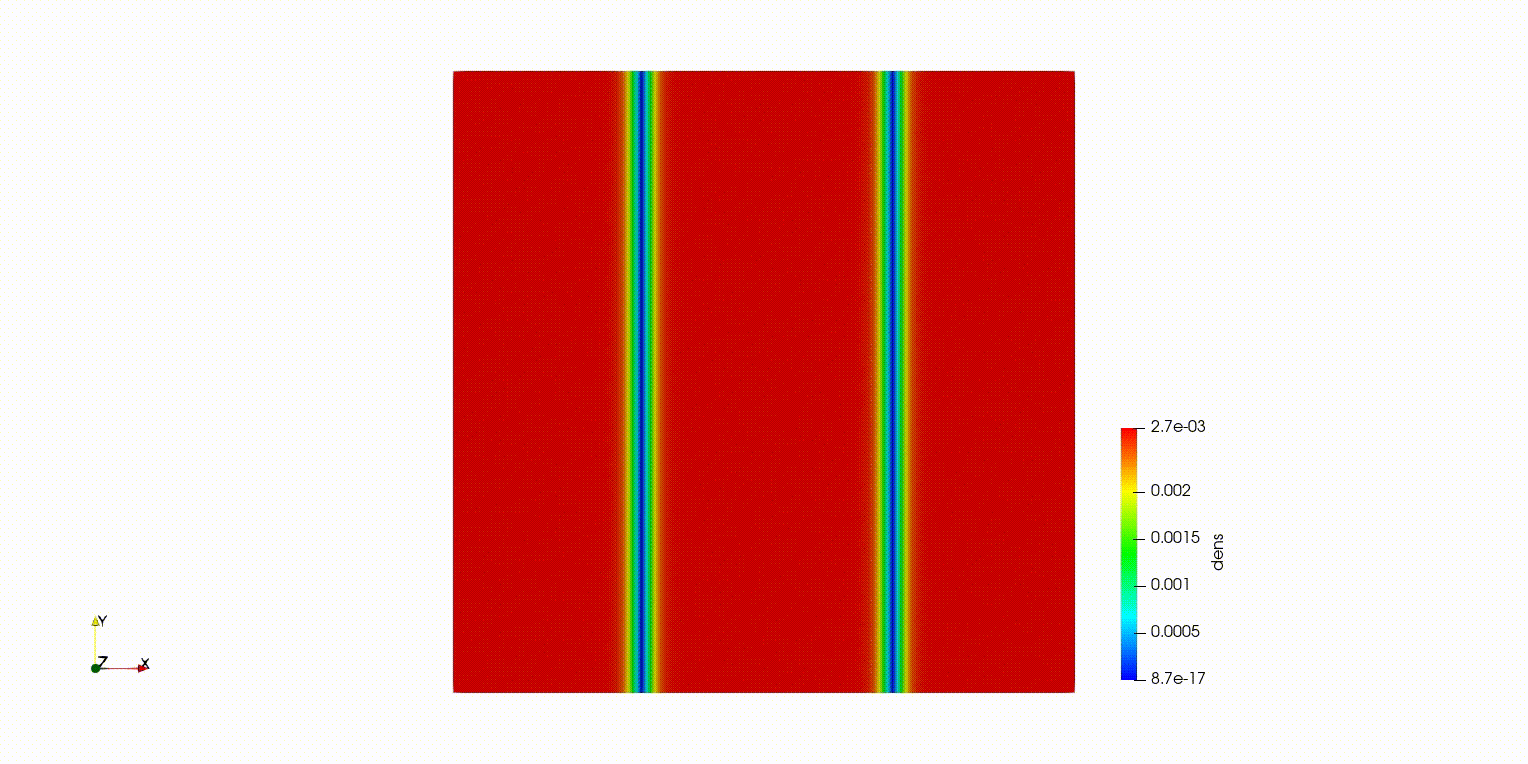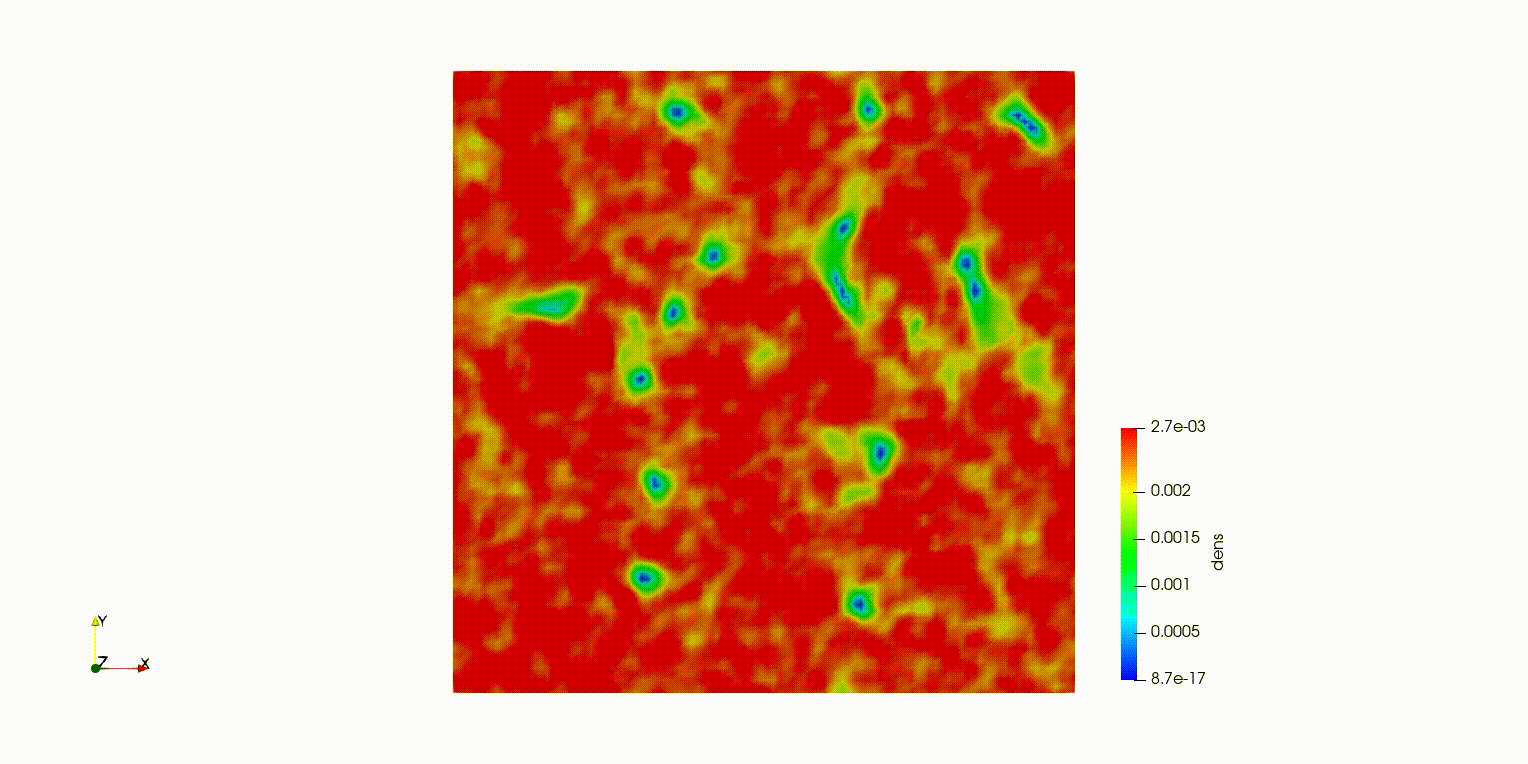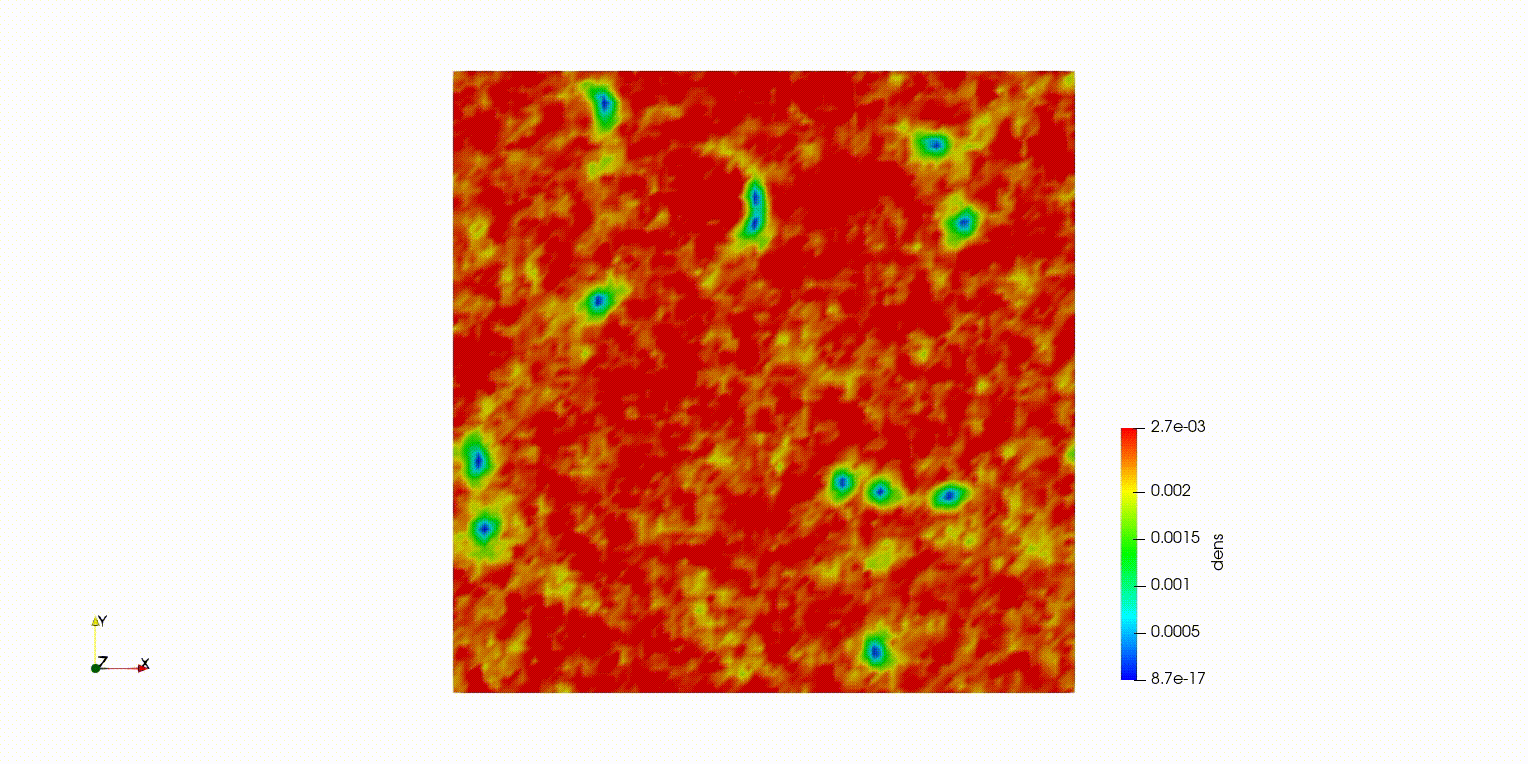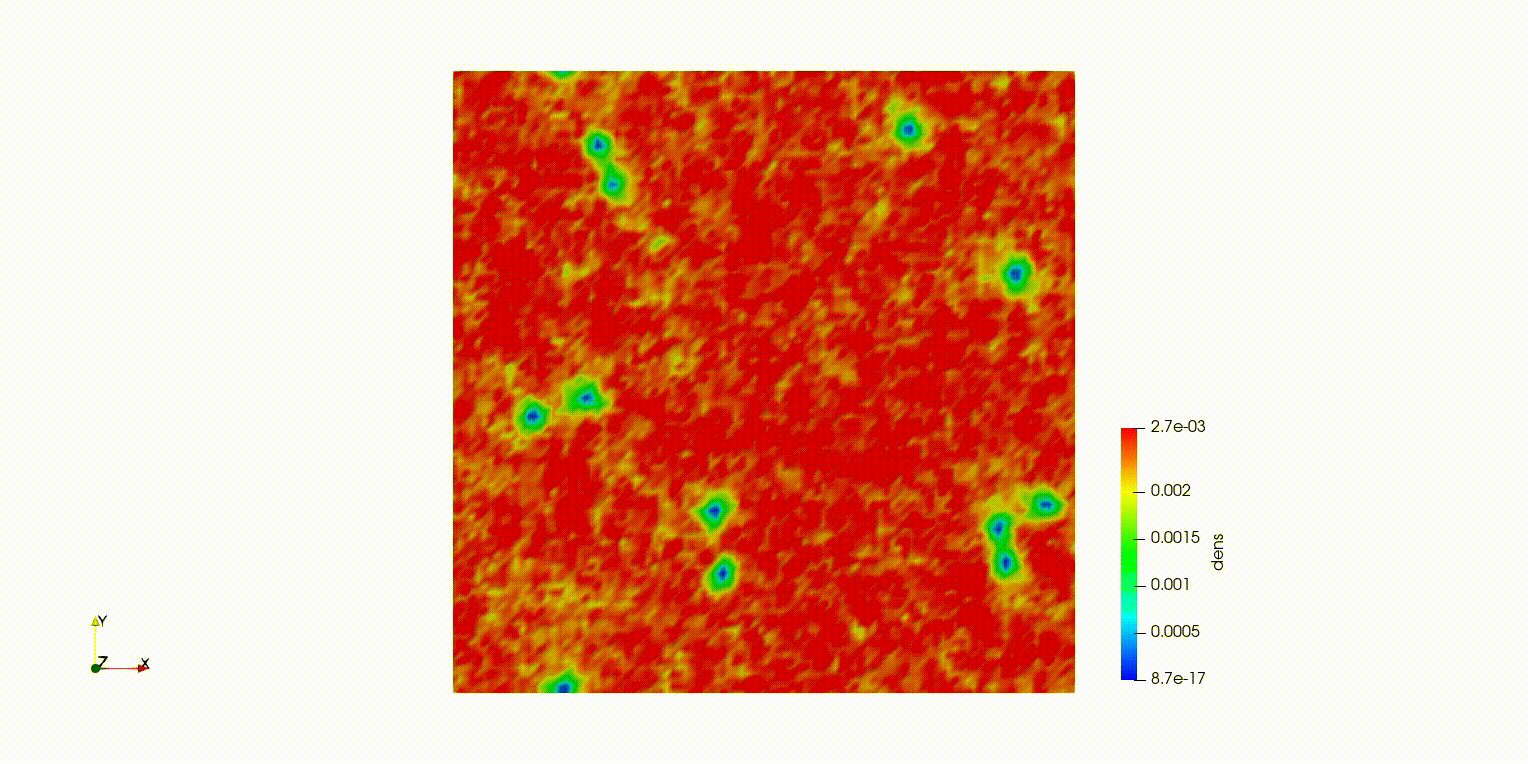
量子流体のソリトン崩壊
量子流体とは、極低温などの条件下で、流体全体が量子力学的な波として振る舞う特殊な流体です。
ダークソリトンはその中に現れる密度の低い安定な波構造ですが、擾乱によって崩壊し、量子渦へと変化していきます。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
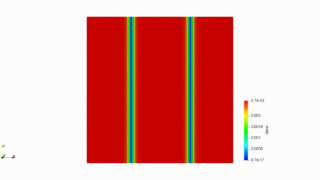
ちなみにこちらをOpenFOAMで実装しようとしたことがあります。
laplacianFoamをカスタマイズしてシュレディンガー方程式の計算ができるように試しましたが、うまくいかず断念(もう少し頑張ればできるかも)
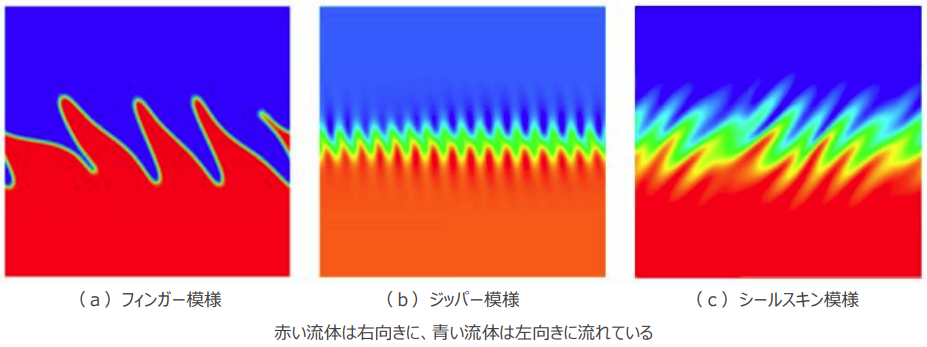
超流動体の界面模様の形成機構
以下の記事の引用です。
流体の粘性が消失した超流動※1 体を想定して、流体力学において基本的な不安定現象である「ケルビン・ヘルムホルツ不安定性」※2 の解析を行い、流体の速度と界面の厚さに依存して様々な界面模様が形成されることを世界で初めて明らかにしました。また、その模様が、「ウェーバー数」※3 と呼ばれる普遍的な定数によって分類できることを明らかにしました。
※1 超流動:流体の粘性が消失した状態を指す。絶対零度近傍の液体ヘリウムや冷却原子気体等がこの性質を示すことが知られている。
※2 ケルビン・ヘルムホルツ不安定性:流体力学上の概念で、層を成しており各層ごとに密度の異なる流体が、お互いに異なる速度で水平運動するときに発生する。大気中でみられる波状雲や木星で観測される大赤斑(渦巻き模様)などがこの不安定性により形成すると考えられている。
※3 ウェーバー数:流れの慣性力と表面張力の比を表す無次元量。
まとめ
本記事では、流体解析で現れるさまざまな不安定性現象を紹介しました。
これらは「美しい可視化ができる」という点だけでなく、オープンCAEのOpenFOAMを使って何を学ぶか、という題材として非常に適しています。
また、途中では一見すると流体力学と距離がありそうな題材も取り上げました。
量子流体は量子力学的効果による流体現象ですが、不安定性や渦構造には古典流体との明確なアナロジーがあります。
宇宙スケールの現象も同様に、圧縮性流体として捉えれば流体力学の枠組みで議論できます。
OpenCAE を手に入れて、「何を題材に解析を始めようか」と考えたとき、
ここで挙げた不安定性現象は魅力的な対象だと考えています。
そのほかに美しい物理現象があれば、集めてみたいですね。
たとえばフラクタル構造など・・・・これも美しい。

OpenCAE学会 学会誌
オープンCAE学会の学会誌(秋号)が出ました。
この中で「オープンCAEによる自己啓発のススメ」というタイトルで執筆させていただきました。

ちなみに表紙は私が書いた絵ですね。

本記事で書いたような流体の美しい現象を再現するというのは、勉強のモチベーションを幾分か上げてくれるのでお勧めです。
BOOTHで学会誌を買う人は稀かもしれませんが、どうしても読みたいよという方は、オープンCAE学会の会員になることをお勧めします。各種講習会の割引に加えて季節ごとに発行される(4か月に1回)学会誌も読むことができる権限を手に入れることができ、大変お得です。