恒等変換から無限小変換｜宇宙に入ったカマキリ

本日の内容は、恒等変換から無限小変換という内容をやっていこうと思います。

恒等変換って何ですか？

無限小変換って何ですか？

というのがあることでしょう。

まずは、恒等変換の復習から紹介して、無限小変換の内容に移りたいと思います(^^)/

恒等変換とは？
無限小変換
無限小変換
無限小変換の公式
1. (14)式より
2. (15)式より
まとめ

恒等変換とは？

ここではざっくり恒等変換についてお話します。

詳しい内容は↓こちらの記事を見て頂いた方が良いのです。

正準変換が一般的な解析力学の枠組みの中での変数変換だとすると、点変換は正準変換の一部であり、恒等変換は点変換の一部であります。

恒等変換は、上記の図のように、新しい変数\(Q_{i}\),\(P_{i}\)は元の変数\(q_{i}\),\(p_{i}\)で書けるような変換のことを言います。

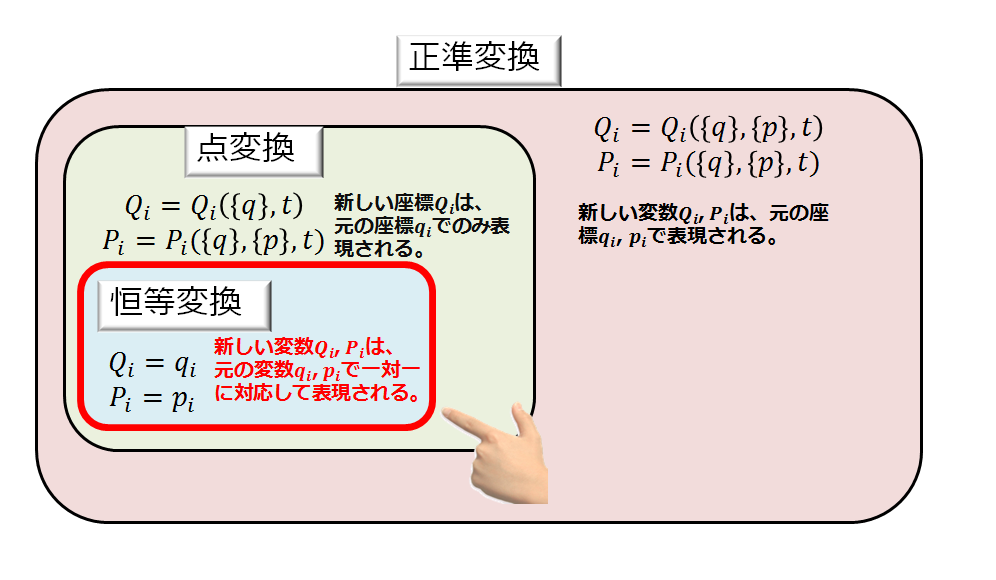
つまり、恒等変換とは正準変換した後の新しい変数\(Q_{i}\),\(P_{i}\)は、

\begin{align*}Q_{i}=q_{i}\cdot\cdot\cdot (1)\end{align*}

\begin{align*}P_{i}=p_{i}\cdot\cdot\cdot (2)\end{align*}

となるような変換であることを意味しています。

正準変換は変数変換した際にもハミルトンの正準方程式を満足するような変換ですが（下記の(5)(6)）、その際には(7)式のように「元のハミルトニアンと新しい変数に対するハミルトニアン」には母関数を介して関係性があります。

\begin{align*}\frac{dq_{i}}{dt}=\frac{\partial H}{\partial p_{i}}\cdot\cdot\cdot (2)\end{align*}

\begin{align*}\frac{dp_{i}}{dt}=-\frac{\partial H}{\partial q_{i}}\cdot\cdot\cdot (4)\end{align*}

\begin{align*}\frac{dQ_{i}}{dt}=\frac{\partial {H}’}{\partial P_{i}}\cdot\cdot\cdot (5)\end{align*}

\begin{align*}\frac{dP_{i}}{dt}=-\frac{\partial {H}’}{\partial Q_{i}}\cdot\cdot\cdot (6)\end{align*}

\begin{align*}H={H}’+\frac{\partial W_{2}}{\partial t}\cdot\cdot\cdot (7)\end{align*}

そして、

母関数

\begin{align*}W_{2}(\{q\},\{P\},t)=\sum_{i}q_{i}P_{i}\cdot\cdot\cdot (8)\end{align*}

点変換による「新しい座標」と「新しい運動量」の関係式

\begin{align*}Q_{i}=q_{i}\cdot\cdot\cdot (9)\end{align*}

\begin{align*}P_{i}=p_{i}\cdot\cdot\cdot (10)\end{align*}

このような変換のことを特に恒等変換と呼びます。

無限小変換

それでは、自由度\(f\)で元の変数（\(\{q\},\{p\}\)）から微小な変化を起こしたとします。

添え字\(i\)の変数について、

\begin{align*}(q_{i},p_{i})→(q_{i}+dq_{i},p_{i}+dp_{i})\cdot\cdot\cdot (8)\end{align*}

となったとします。

これは、恒等変換のところでもやりましたが、位相空間内をハミルトニアンの正準方程式を満足しながら動くことになるので、

\(Q_{i},P_{i}\)は\(q_{i},p_{i}\)からの微小変化による正準変換であるという解釈すれば、

\begin{align*}(q_{i}+dq_{i},p_{i}+dp_{i})\end{align*}

は、結局

\begin{align*}Q_{i}=q_{i}+dq_{i}\cdot\cdot\cdot (9)\end{align*}

\begin{align*}P_{i}=p_{i}+dp_{i}\cdot\cdot\cdot (10)\end{align*}

とおいても同じ考え方になります。

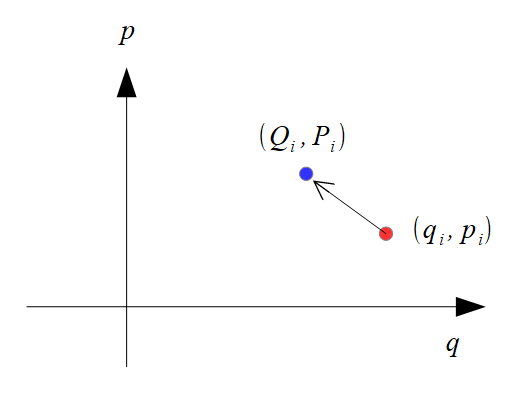
これを無限小変換と呼びます。

無限小変換

このように無限小変換を行ったとき、母関数はどうなっているのでしょうか？

もちろん(8)式から少し変わることが予想されます。

\begin{align*}{W}’_{2}=W_{2}+dW_{2}\cdot\cdot\cdot (11)\end{align*}

となったとしましょう。

(8)式より、母関数\(W_{2}\)の変数は\(\{q\},\{P\}\)でしたから当然\(dW_{2}\)も\(\{q\},\{P\}\)を変数とした関数であります。

であるので母関数の微小変化分は、変数\(\{q\},\{P\}\)を持つ関数\(G\)を導入して、

\begin{align*}dW_{2}=\epsilon\cdot G(\{q\},\{P\})\cdot\cdot\cdot (12)\end{align*}

と書くことにします。

この時、

\begin{align*}{W}’_{2}(\{q\},\{P\},t)=\sum_{i}q_{i}P_{i}+\epsilon\cdot G(\{q\},\{P\})\cdot\cdot\cdot (13)\end{align*}

変数を書かない方が見やすいかもしれませんね(‘_’)

\begin{align*}{W}’_{2}=\sum_{i}q_{i}P_{i}+\epsilon\cdot G(\{q\},\{P\})\cdot\cdot\cdot (13)\end{align*}

\(\epsilon\)は無限小パラメータと呼ばれるものです。

この無限小パラメータはとても便利です。

もし、

\begin{align*}(q_{i},p_{i})→(q_{i}+dq_{i},p_{i}+dp_{i})\cdot\cdot\cdot (8)\end{align*}

の変化が、

「時間の変化に対してであれば：微小時間変化\(\epsilon=dt\)」

「空間の変化に対してであれば：微小空間変化\(\epsilon=dq\)」

「回転の変化に対してであれば：微小角度変化\(\epsilon=d\theta\)」

という解釈になるので、とても一般性があります。

無限小変換の公式

さて、このように無限小変換を向けた際の、他の変数(\(Q_{i},p_{i}\))はどうなっているのでしょうか？

その際の変換公式は↑で勉強したので、結果だけ書きましょう(^^)

\begin{align*}Q_{i}=\frac{\partial {W}’_{2}}{\partial P_{i}}\cdot\cdot\cdot (14)\end{align*}

\begin{align*}p_{i}=\frac{\partial {W}’_{2}}{\partial P_{i}}\cdot\cdot\cdot (15)\end{align*}

\(q_{i},P_{i}\)を変数とする母関数に対しては↑こんな感じの関係式があったのです。

(14)式より

\begin{align*}Q_{i}=\frac{\partial {W}’_{2}}{\partial P_{i}}=\frac{\partial }{\partial P_{i}}\big(\sum_{i}q_{i}P_{i}+\epsilon\cdot G(\{q\},\{P\})\big)\cdot\cdot\cdot (16)\end{align*}

⇔

\begin{align*}Q_{i}=q_{i}+\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial P_{i}}\cdot\cdot\cdot (17)\end{align*}

⇔(恒等変換なので(2)式より)

\begin{align*}Q_{i}=q_{i}+\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial p_{i}}\cdot\cdot\cdot (18)\end{align*}

ここで、

\begin{align*}Q_{i}=q_{i}+dq_{i}\cdot\cdot\cdot (9)\end{align*}

であるので(18)式は、

\begin{align*}dq_{i}=\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial p_{i}}\cdot\cdot\cdot (19)\end{align*}

(15)式より

\begin{align*}p_{i}=\frac{\partial {W}’_{2}}{\partial q_{i}}=\frac{\partial }{\partial q_{i}}\big(\sum_{i}q_{i}P_{i}+\epsilon\cdot G(\{q\},\{P\})\big)\cdot\cdot\cdot (20)\end{align*}

⇔

\begin{align*}p_{i}=P_{i}+\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial q_{i}}\cdot\cdot\cdot (21)\end{align*}

ここで、

\begin{align*}P_{i}=p_{i}+dp_{i}\cdot\cdot\cdot (10)\end{align*}

であるので(21)式は、

\begin{align*}dp_{i}=-\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial q_{i}}\cdot\cdot\cdot (22)\end{align*}

まとめ

無限小変換を行うことにより、

\begin{align*}dq_{i}=\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial p_{i}}\cdot\cdot\cdot (19)\end{align*}

\begin{align*}dp_{i}=-\epsilon\cdot \frac{\partial G(\{q\},\{P\})}{\partial q_{i}}\cdot\cdot\cdot (22)\end{align*}

という関係式が出てきました(^^)

変数を書くと見にくいので、書かないようにしてみましょうか。

\begin{align*}dq_{i}=\epsilon\cdot \frac{\partial G}{\partial p_{i}}\cdot\cdot\cdot (19)\end{align*}

\begin{align*}dp_{i}=-\epsilon\cdot \frac{\partial G}{\partial q_{i}}\cdot\cdot\cdot (22)\end{align*}

これを見ると何かの形に似ているではありませんか(‘_’)

そうです！！ハミルトニアン正準方程式です。

\begin{align*}(q_{i},p_{i})→(q_{i}+dq_{i},p_{i}+dp_{i})\cdot\cdot\cdot (8)\end{align*}

の変化が、「時間の変化に対してであれば：微小時間変化\(\epsilon=dt\)」

これは、「微小時間\(dt\)での間に、位相空間上を(\(q_{i},p_{i}\))→(\(q_{i}+dq_{i},p_{i}+dp_{i}\))と変化しながら運動する」という解釈になります。