どうも(^^)/
本記事では、量子力学的効果によって出現する量子流体についてのお話をしたいと思います。
- 量子流体とは何か
- ボース粒子、フェルミ粒子についての特徴
- ボース・アインシュタイン凝縮
これらの内容を本格的に学ぼうと思うと、主に統計力学と量子力学の知識が必要になってきます。しかし、本記事ではできるだけイメージをわかりやすく解説し、量子流体とはどういった物理を対象にしているのかを理解してもらうことを目的としておきます(^^)
ですので、難しい数式は出てきません(^^)/
ということで、本記事の内容は以下となっております。
- ボース・アインシュタイン凝縮よる量子力学的効果によって出現する量子流体とは何か?
- 量子流体はどんな方程式に従う現象であるのか?
量子流体とは
まず、量子流体とはなんなのか?
量子力学的効果によって出現する流体力学のことを量子流体と呼んでいます。量子力学というと、光、あるいは原子や素粒子などの小さな粒子を対象にした理論であり、ニュートン力学では記述することのできない現象を取り扱うときに使いますよね。
しかし、量子力学を使う場面というのは、系が小さいというだけではなく、温度が非常に小さい場合においてもその効果を発揮するのです。
その時に肝となる考え方は、「同種粒子は区別しない」ということです。
フェルミ粒子とボース粒子
前回の記事でも解説した通り、同種粒子(粒子の区別はしない)というのが、低温状態で重要となる考え方であり、そこからフェルミ粒子とボース粒子の2種類の粒子が存在することを示しました。
記事を読んでいない方のために、さらっとフェルミ粒子とボース粒子の違いを解説しておきましょう(^^)/
フェルミ粒子:1つのエネルギー準位に1つの状態しか所有できない
フェルミ粒子は、1つのエネルギー準位にはひとつの粒子状態しか入ることができないという制約があります。これをパウリの排他律といいます。
エネルギー状態が高いよりも低い状態の方が安定であるために、下の方から粒子が埋められていくということになります。
※高温状態であれば、粒子がエネルギー準位を1つ超えるのは簡単で、必ずしも下から順番に埋め尽くされていくというわけではありません・・・
低温状態になると、基本的に粒子状態は下から埋めていくことになります。
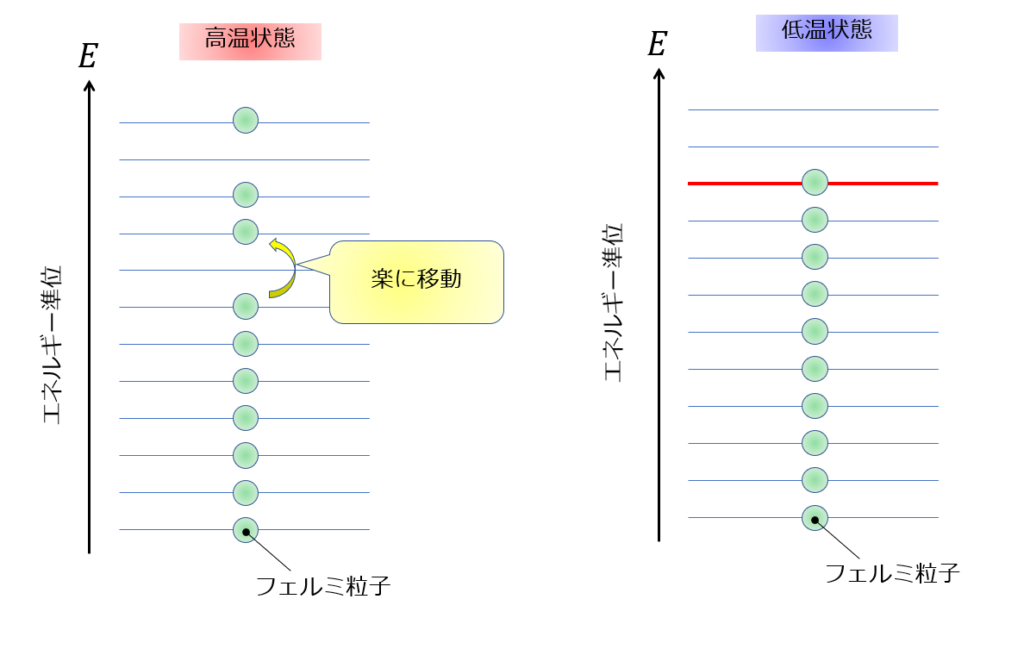
これがフェルミ粒子についての特徴です・・・これ以上深堀した話はしません(‘ω’)ノ
ボース粒子:1つのエネルギー状態に何個でも粒子を所有できる
フェルミ粒子にはパウリの排他律のように、各エネルギー準位に所有できる粒子状態に制限があった(1つの状態だけ)のですが、
ボース粒子にはその制限がありません。
高温状態であれば、どのエネルギー準位も行き放題で色んな粒子状態を眺めても色々な状態をとっているということになります。
低温状態では、大多数の粒子が最低エネルギー準位に落ち込むということが起こるのです。
これがボースアインシュタイン凝縮と呼ばれるものです。

凝縮というと、実空間の一点に集まっているという印象を受けるかもしれませんが、ここでいう”凝縮”とは運動量空間における凝縮を意味しています。
運動量空間における凝縮とは、「運動量空間のある一点に状態が集まっている=全ての粒子状態が同じ状態である」という意味なのです。
これがボース・アインシュタイ凝縮の”凝縮”の意味です。
ボース・アインシュタイン凝縮体の秩序変数
低温状態にすると、
- 最低のエネルギー準位に大多数の粒子状態を所有することになる
- 粒子の個性が消える
- 大多数の粒子がひとつの状態で記述することができる
というのをマンガ絵で理解しやすいように表現してみます。
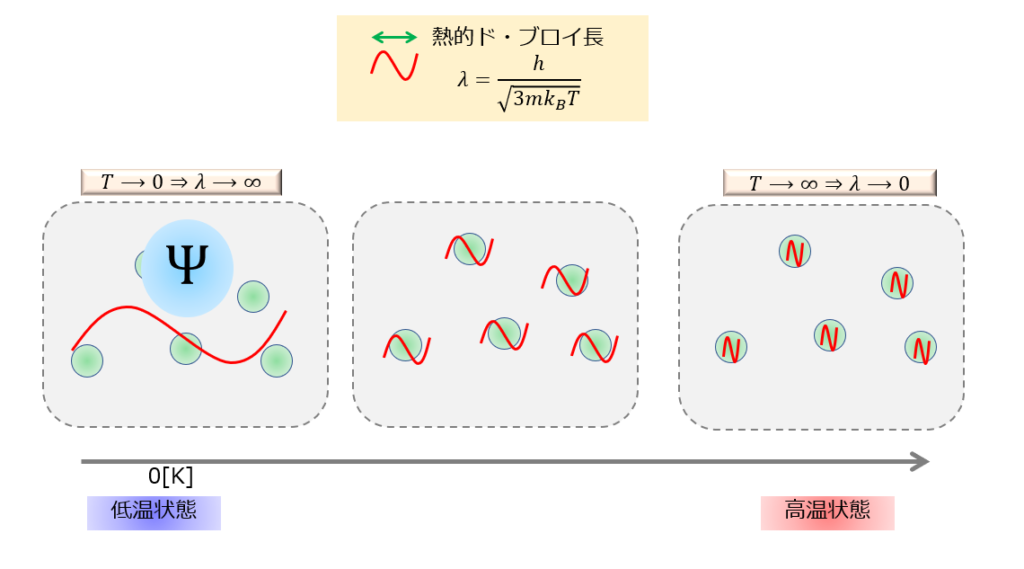
低温にすると大多数の粒子が同じ状態に落ち込むため、粒子の個性というのが消えて大多数の粒子が同じ状態であるために、1つの波動関数\(\psi\)で記述できるようになるということです。
これがボース・アインシュタイ凝縮であり、量子流体の舞台となります。
言い換えると、これが低温状態で出現する量子力学的による波(流体)の性質を持った量子流体というわけです。
グロス・ピタエフスキー方程式(Gross Pitaevskii equation)
ここでは、低温状態でボース・アインシュタイン凝縮を起こした多体粒子の系は一体どのように記述されるのかというのを考えます。
先ほどの例でわかったことは、大多数の粒子達が同じ最低エネルギー状態に落ち込んだということより、1つの波動関数\(\psi\)と書けるということです。
では、この波動関数がどのような方程式に従うのでしょうか?
今から示す方程式のポイントは3つです。
- ボース・アインシュタイ凝縮を起こしているので、大多数の粒子の状態をまとめて1つの波動関数\(\psi\)と書く。
- ボース・アインシュタイ凝縮を起こした大多数の粒子を捕獲ポテンシャルで捕獲する。
捕獲ポテンシャル:(\(V_{ext}=\frac{m\omega^2\boldsymbol{r}^2}{2}\)) - 粒子間の相互作用は近接でのみ作用する(\(U_{int}=g\delta(\boldsymbol{r_{1}}-\boldsymbol{r_{2}})\))
※近接のみ作用するというのは希薄な気体であるという意味です。
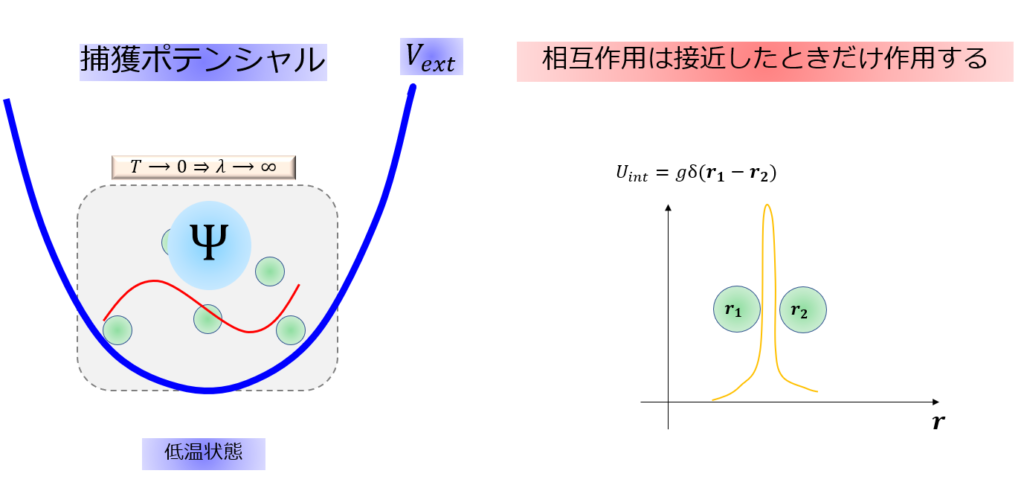
これを、低温状態で出現する「捕獲ポテンシャルに閉じ困られた希薄原子気体のボース・アインシュタイ凝縮体」と呼びます。
呼び名を簡単に、希薄原子気体BECと呼ばれたりします。
※BECは、Bose-Einstein Condensate(ボース・アインシュタイン凝縮体)の略です。
では、この希薄原子気体が従う方程式は何なのか??
それが、こちらです。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r})}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{1}
\end{align*}
量子力学で超有名なシュレディンガー方程式じゃないかと思ったかもしれませんが、シュレディンガー方程式とは式の上では少し違うのですが、根本的な意味が異なります。
- 式は少し違う

ご覧の通り、ほぼシュレディンガー方程式なのですが、最後の項に粒子間相互作用の項があります。しかも、\(\psi\)の2乗に波動関数が掛けられているので、これは非線形項です。
ですから、これは非線形シュレディンガー方程式とも呼ばれます。
- シュレディンガー方程式と根本的な意味が異なる
シュレディンガー方程式とグロス・ピタエフスキー方程式は、根本的な意味で異なるのです。
シュレディンガー方程式
まず、シュレディンガー方程式は1つの粒子の存在確率を\(|\psi(\boldsymbol{r})|^2\)で表現しています。
ですので、全空間で積分すると確率は1になるというものですよね。
\int |\psi(\boldsymbol{r})|^2dr^3\tag{2}
\end{align*}
つまり、シュレディンガー方程式は粒子の存在確率の時間発展を示す方程式であるということです。
グロス・ピタエフスキー方程式
しかし、希薄原子気体BECが従うグロス・ピタエフスキー方程式は、粒子数密度(凝縮体密度)\(n(\boldsymbol{r})\)と位相\(\theta(\boldsymbol{r})\)とで特徴づけられる波動関数\(\psi(\boldsymbol{r})\)の時間発展を示す方程式なのです。
つまり、波動関数は、
\psi(\boldsymbol{r})|=\sqrt{n(\boldsymbol{r})}e^{i\theta(\boldsymbol{r})}\tag{3}
\end{align*}
と書くことにより粒子数密度\(|\psi(\boldsymbol{r})|^2=n(\boldsymbol{r})\)を表現していることになります。
ですので、全空間で積分すると全粒子数になるというものです。
\int |\psi(\boldsymbol{r})|^2dr^3=N\tag{2}
\end{align*}
このグロス・ピタエフスキー方程式
i\hbar\frac{\partial \psi(\boldsymbol{r})}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{1}
\end{align*}
を解くことにより、低温状態で出現するボース・アインシュタイ凝縮体である量子流体の物理現象を再現できるというものなのです(^^)/
まとめ
温度が非常に小さい場合に、量子力学的効果によって出現する流体は量子流体と呼ばれています。その現象の舞台となるのは、低温状態で出現するボース・アインシュタイ凝縮によるものです。
ボース・アインシュタイ凝縮によって、最低エネルギー準位に大多数の粒子が落ち込むことにより、大多数の粒子を1つの波動関数(秩序変数)\(\psi(\boldsymbol{r})\)で記述でき、以下の方程式に従います。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
ただし、グロス・ピタエフスキー方程式は以下の状況を仮定していることに注意。
- ボース・アインシュタイ凝縮を起こしているので、大多数の粒子の状態をまとめて1つの波動関数\(\psi\)と書く。
- ボース・アインシュタイ凝縮を起こした大多数の粒子を捕獲ポテンシャルで捕獲する。
捕獲ポテンシャル:(\(V_{ext}=\frac{m\omega^2\boldsymbol{r}^2}{2}\)) - 粒子間の相互作用は近接でのみ作用する(\(U_{int}=g\delta(\boldsymbol{r_{1}}-\boldsymbol{r_{2}})\))
※近接のみ作用するというのは希薄な気体であるという意味です。
超流動へリムもグロス・ピタエフスキー方程式に従うのか
超流動ヘリウムは、低温状態で出現する粘性のない流体現象ですが、さきほどのグロス・ピタエフスキー方程式では上手く記述できないという点があります。
超流動ヘリウムは、グロス・ピタエフスキー方程式での以下の仮定が成立しないのです。
- 粒子間の相互作用は近接でのみ作用する(\(U_{int}=g\delta(\boldsymbol{r_{1}}-\boldsymbol{r_{2}})\))
※近接のみ作用するというのは希薄な気体であるという意味です。
つまり、粒子間の相互作用が強いためグロス・ピタエフスキー方程式では記述できないということになります。