どうも、こんちには(@t_kun_kamakiri)(^^)/
↓こちらの記事で量子流体が従う方程式であるグロス・ピタエフシキー方程式(いわゆる非線形シュレディンガー方程式)での速度場を定義しました。
グロス・ピタエフスキー方程式(略してGP方程式)
\begin{align*}
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
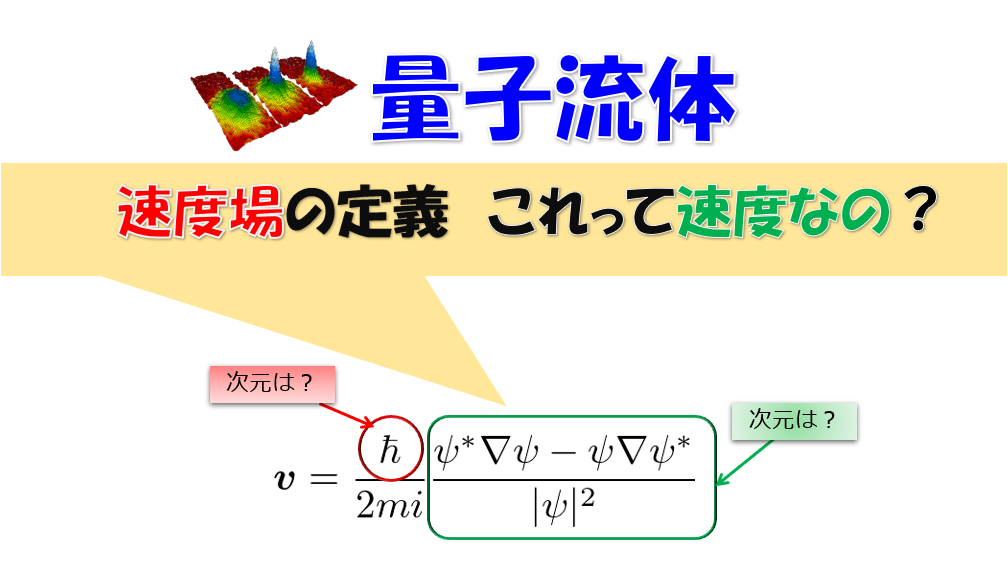
から、凝縮体の波動関数(秩序変数)を\(\psi=\sqrt{n}e^{i\theta}\)とおき、速度場を、速度場
\begin{align*}
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\tag{2}
\end{align*}
というように定義。
ここで、速度場というからには(2)式が速度の次元(単位)持っていてほしいですよね?
速度の次元(単位)とは?
まず速度の単位ってどう書いていたかを確認しましょう。
単位の表記はSI単位系とします。
| 基本単位 | 次元 | 記号 |
|---|---|---|
| 名称 | ||
|
長さ メートル(metre) |
m | L |
|
質量 キログラム(kilogram) |
kg | M |
|
時間 秒(second) |
s | T |
|
電流 アンペア(ampere) |
A | I |
|
熱力学温度 ケルビン(kelvin) |
K | θ |
|
物質量 モル(mole) |
mol | N |
|
光度 カンデラ(Candela) |
cd | J |
これを使うと速度の次元は(m/s)だから、
速度の次元:\(LT^{-1}\)
となります。
\(\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\)の次元をどう考えるか?
速度場
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\tag{2}
\end{align*}
の次元が速度の次元をもっているのかを調べます。
しかし、「この次元って何なの?」ってことになります。
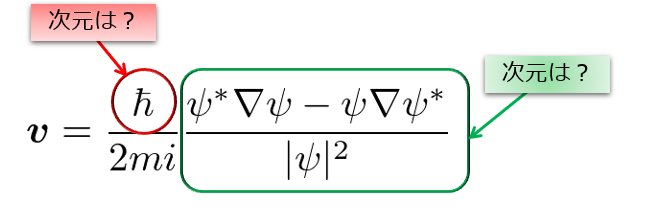
少し落ち着いて考えてみましょう(^^)/
プランク定数の次元を考える
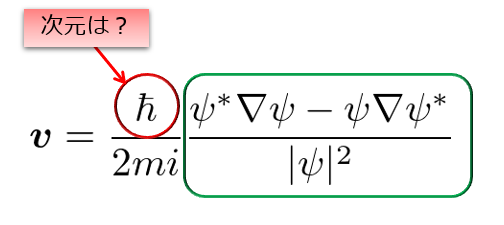
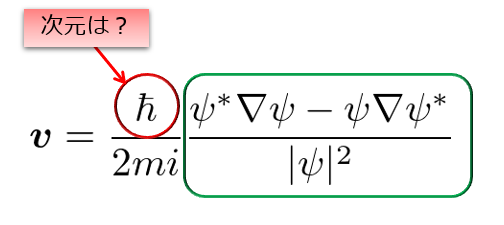
まず、プランク定数の次元を考えましょう。
方程式は常に同じ次元で結ばれている
例えば物理の問題を解いていて、
\(E=\frac{1}{2}mv\)や、\(p=v\)など次元の異なるものを見かけたことがないと思います。
※\(E\):エネルギー
※\(p\):運動量
※\(m\):質量
※\(v\):速度
だから、\(\hbar=\frac{h}{2\pi}\)(\(h\)がプランク定数)の単位がわからなかったとしても、プランク定数が使われている式を思い出せばよいということになります。
例1 プランク定数の次元を調べよう 不確定性原理
不確定性原理は「位置」と「運動量」を同時に観測できないという量子力学における基本原理ですよね。
不確定性原理の不等式を思い浮かべて・・・
\Delta p\cdot\Delta x \geq \frac{\hbar}{2}\tag{3}
\end{align*}
お!!
\(\hbar=\frac{h}{2\pi}\)だから、プランク定数の次元は「運動量×距離」か!!
というのがわかります。
ここで、
- 運動量\(p\)の次元:\(mv\)
- 位置\(x\)の次元:\(x\rightarrow vt\)
とするなら、プランク定数は次元だけで言うと、\(mv^{2}t\)=「エネルギー×時間」ということになります。
例2 プランク定数の次元を調べよう 光電効果
光電効果もめちゃくちゃ有名ですよね。
「物質に光を照射すると、電子(光電子)が物質の表面から放出される。」ってやつです。
そのときのエネルギーの表記にプランク定数\(h\)使ってたな~っていうのを思い浮かべて・・・
E=h\nu\tag{4}
\end{align*}
これもプランク定数の次元を知るのにはわかりやすいですよね。
振動数\(\nu\)は、時間の逆数の次元を持っているので次元は\(T^{-1}\)です。
ということは、プランク定数の次元は、「エネルギー×時間 かー」ってことになります。
結局プランク定数の次元をSI単位系で書くとどうなるのか?
プランク定数の次元は、「エネルギー×時間」ってことがわかったので、SI単位系で表現すると、
プランク定数の次元:\([M(LT^{-1})^2T]=[ML^{2}T^{-1}]\)
です。
\(\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\)の次元を考える
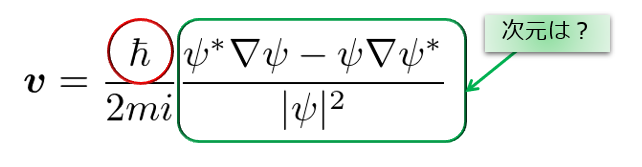
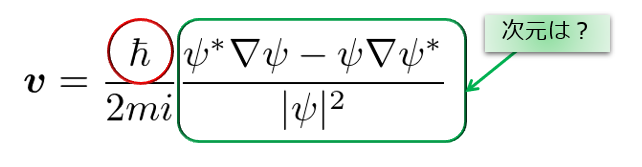
これの次元はどうなるのかを考えます。
ナブラ演算子\(\nabla\)の次元を考える
ややこしいのはナブラ演算子\(\nabla\)の次元を考えることですよね。
\(\nabla=\big(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\big)\)なので、
ナブラ演算子\(\nabla\)の次元は\([L^{-1}]\)
であることがすぐにわかります。
分母分子に\(\psi\)がある
さらに幸いなことに、分母分子に波動関数\(\psi\)というよくわからない次元をもったものがいますが、分母分子に同じ数だけ存在しているので、次元としてはキャンセルされるので、次元を考える必要はありません。
結局\(\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\)の次元をSI単位系で書くとどうなるのか?
\(\psi\)の次元を考えなくてもよいので、結局ナブラ演算子\(\nabla\)の次元だけ考えればよいということになるので、
\(\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\rightarrow [L^{-1}]\)
とシンプルになります。
\(\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\)をSI単位系で書くとどうなるのか?
今までわかった次元をSI単位系で並べてみます。
- プランク定数\(h\)の次元:\([M(LT^{-1})^2T]=[ML^{2}T^{-1}]\)
- \(\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\)の次元:\( [L^{-1}]\)
だから、(2)式の次元をSI単位系で書くと・・・
次元をSI単位系で計算
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\rightarrow ML^{-2}T^{-1}M^{-1}L^{-1}=LT^{-1}\tag{3}
\end{align*}
となります。
ちゃんと速度の次元になりました(^^)/
まとめ
速度場
\boldsymbol{v}=\frac{\hbar}{2mi}\frac{\psi^{*}\nabla\psi-\psi\nabla\psi^{*}}{|\psi|^2}\tag{2}
\end{align*}
のが本当に速度場としての資格を持つのか疑惑をもっていましたが、これはちゃんと速度の次元になっていました。
めでたし、めでたし(^○^)