どうも(^^)/
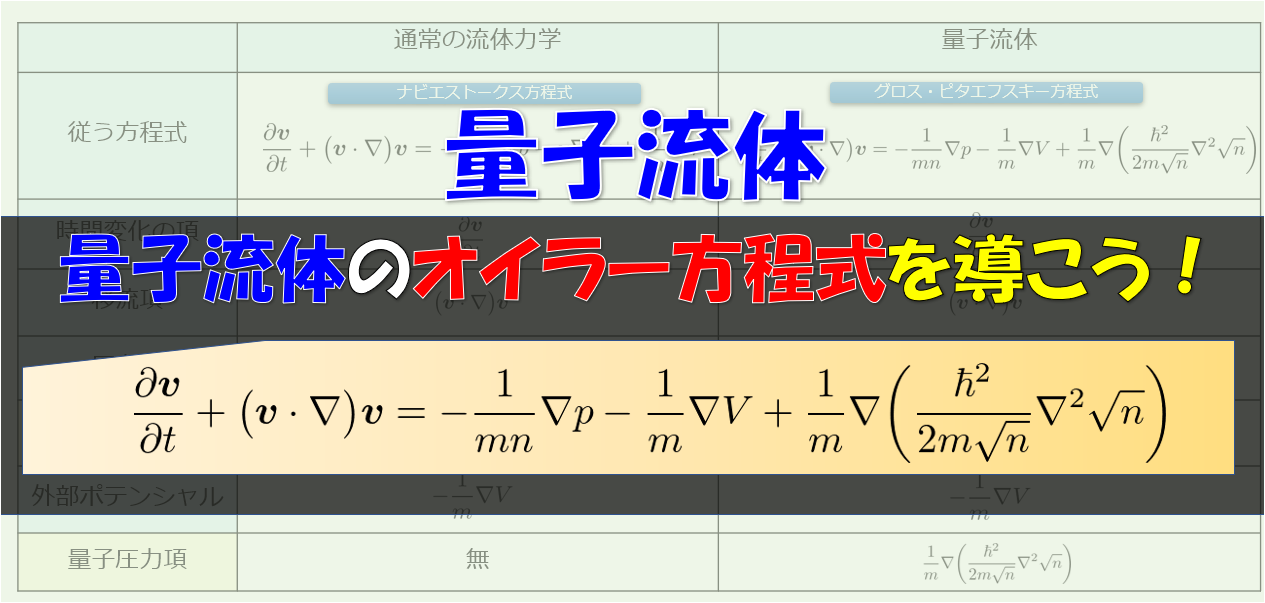
本記事では、量子力学的効果によって出現する量子流体が従う方程式であるグロス・ピタエフスキー方程式(非線形シュレディンガー方程式)から、非粘性の流体力学でよく見られるオイラー方程式(みたいな方程式)を導きたいと思います。
結論を先に示しておきます。
グロス・ピタエフスキー方程式(略してGP方程式)
\begin{align*}
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}オイラー方程式(量子流体バージョン)
\begin{align*}
\frac{\partial \boldsymbol{v}}{\partial t}+\big(\boldsymbol{v}\cdot\nabla\big)\boldsymbol{v}=-\frac{1}{mn}\nabla p-\frac{1}{m}\nabla V+\frac{1}{m}\nabla\bigg(\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{2}
\end{align*}
もしくは、\begin{align*}
\frac{\partial \boldsymbol{v}}{\partial t}=-\frac{1}{mn}\nabla p-\nabla\bigg(\frac{\boldsymbol{v}^2}{2}\bigg)-\frac{1}{m}\nabla V+\frac{1}{m}\nabla\bigg(\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{3}
\end{align*}
(1)式はともかく、(2)(3)式は流体力学の「オイラー方程式」ととてもよく似ているでしょ!!
前回の記事はこちら
量子流体が(1)式のGP方程式に従うと言っても・・・”流体”と名を付けている以上はやはり通常の流体力学との類似性などが気になりますよね。
その類似性のひとつが、量子流体もオイラー方程式が成り立つということです。
参考書
前回の記事の復習
前回までに、どのような記事を書いたのかというのを紹介したいと思います。
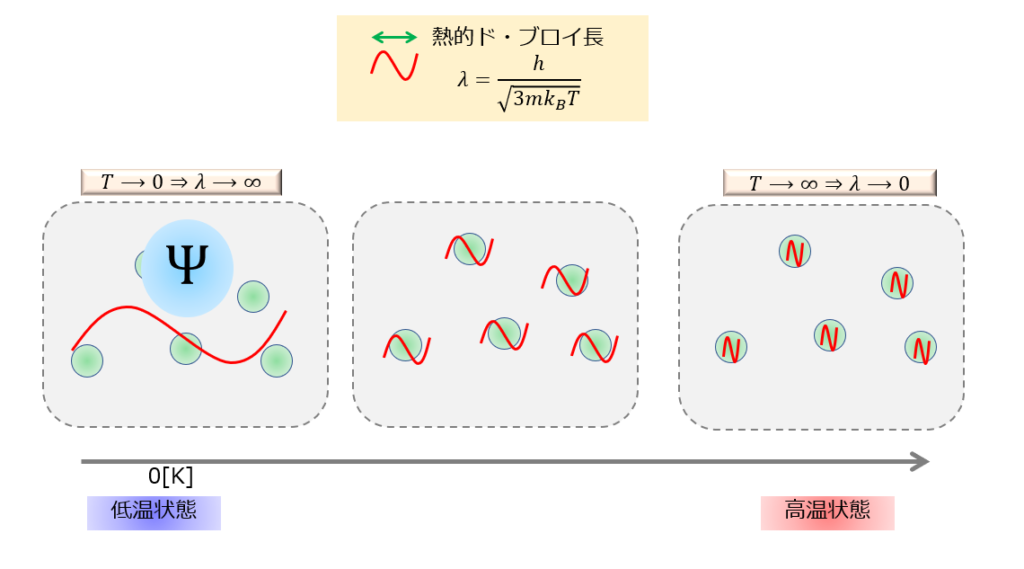
まずは、量子力学の範疇でフェルミ粒子とボース粒子というのがあり、特に重要なのは大多数のボース粒子が非常に小さい温度の場合に、量子力学的効果によって量子流体と呼ばれる流体現象が現れます。
量子流体は、低温状態で出現するボース・アインシュタイ凝縮によるものです。
ボース・アインシュタイ凝縮によって、最低エネルギー準位に大多数の粒子が落ち込むことにより、大多数の粒子を1つの波動関数(秩序変数)\(\psi(\boldsymbol{r})\)で記述でき、以下の方程式に従います。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
ただし、グロス・ピタエフスキー方程式は以下の状況を仮定していることに注意。
- ボース・アインシュタイ凝縮を起こしているので、大多数の粒子の状態をまとめて1つの波動関数\(\psi\)と書く。
- ボース・アインシュタイ凝縮を起こした大多数の粒子を捕獲ポテンシャルで捕獲する。
捕獲ポテンシャル:(\(V_{ext}=\frac{m\omega^2\boldsymbol{r}^2}{2}\)) - 粒子間の相互作用は近接でのみ作用する(\(U_{int}=g\delta(\boldsymbol{r_{1}}-\boldsymbol{r_{2}})\))
※近接のみ作用するというのは希薄な気体であるという意味です。
量子流体というからには、通常の流体力学の方程式との類似性が気になるところですよね。
前回は、量子流体が従う方程式であるグロス・ピタエフスキー方程式から、速度場を定義することにより、連続の式を導くことができました。
グロス・ピタエフスキー方程式(略してGP方程式)
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}
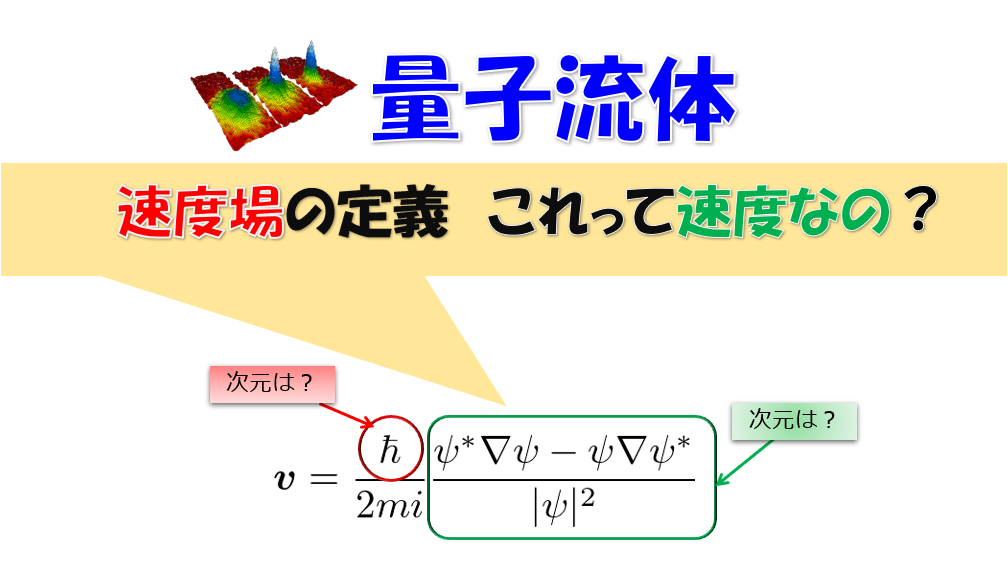
から、凝縮体の波動関数(秩序変数)を\(\psi=\sqrt{n}e^{i\theta}\)とおき、速度場を、
速度場
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{10}
\end{align*}
と定義することにより、以下のような連続の式を導出することができました。
連続の式
\frac{\partial n}{\partial t}+\nabla\cdot\big(n\boldsymbol{v})=0\tag{8}
\end{align*}
わかりやすい論文も見つけたので、↓こちらもどうぞ
The Gross-Pitaevskii Equation and Bose-Einstein condensates
Gross-Pitaevskii方程式から「オイラー方程式」を導く
さて、量子流体における(2)or(3)式のようなオイラー方程式(みたいな式)を導くにあたって、何からスタートしようかということを考えます。
使える方程式は、下記のGP方程式・・・
i\hbar\frac{\partial \psi}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi+V_{ex}\psi(\boldsymbol{r},t)+g|\psi|^2\psi\tag{4}
\end{align*}
※変数\(\boldsymbol{r},t)\)があると、式変形が煩雑に見えますので、\(\psi(\boldsymbol{r},t)=\psi\)と表記することにします。
凝縮体の波動関数(秩序変数)を\(\psi=\sqrt{n}e^{i\theta}\)とおくことで定義される下記の速度場・・・
速度場
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{5}
\end{align*}
使えるのは、こんなところでしょう。
ルートがあると煩雑になるので、\(f(\boldsymbol{r},t)=\sqrt{n(\boldsymbol{r},t)}\)とおいて、
\psi=fe^{i\theta}\tag{6}
\end{align*}
※\(f\)と\(\theta\)は実数
この(6)式を(4)式のGP方程式に代入するところからやっていきましょう。
丁寧に計算しないと結構ごちゃごちゃしていきます・・・・
GP方程式の左辺
GP方程式の左辺を計算します。
左辺
i\hbar\frac{\partial \psi}{\partial t}=i\hbar\frac{\partial f}{\partial t}e^{i\theta}-\hbar f\frac{\partial \theta}{\partial t}e^{i\theta}\tag{7}
\end{align*}
GP方程式の右辺
GP方程式の左辺を計算します。
右辺
-\frac{\hbar^2}{2m}\nabla^2\psi=-\frac{\hbar^2}{2m}\bigg(\nabla^2f-\big(\nabla\theta\big)^2f+i\big(\nabla^2\theta\big)f+2i\big(\nabla\theta\big)\cdot\nabla f\bigg)e^{i\theta}+V_{ex}fe^{i\theta}+g|f|^2fe^{i\theta}\tag{8}
\end{align*}
式は少し煩雑ですが、丁寧にまとめれば大丈夫でしょう。
実部と虚部に分ける
(7)(8)式は、(4)式でイコールで結ばれているので、まずはイコールで結んで書き下しましょう。
i\hbar\frac{\partial f}{\partial t}e^{i\theta}-\hbar f\frac{\partial \theta}{\partial t}e^{i\theta}=-\frac{\hbar^2}{2m}\bigg(\nabla^2f-\big(\nabla\theta\big)^2f+i\big(\nabla^2\theta\big)f+2i\big(\nabla\theta\big)\cdot\nabla f\bigg)e^{i\theta}+V_{ex}fe^{i\theta}+g|f|^2fe^{i\theta}\tag{9}
\end{align*}
これでは、煩雑すぎてよくわからないので、(9)式の両辺を\(e^{i\theta}\)で割り、実部と虚部に分けることにします。
i\biggl\{\hbar\frac{\partial f}{\partial t}\biggr\}+\biggl\{-\hbar f\frac{\partial \theta}{\partial t}\biggr\}=i\biggl\{-\frac{\hbar^2}{2m}\bigg(\big(\nabla^2\theta\big)f+2\big(\nabla\theta\big)\cdot\nabla f\bigg)\biggr\}+\biggl\{-\frac{\hbar^2}{2m}\bigg(\nabla^2f-\big(\nabla\theta\big)^2f+V_{ex}f+g|f|^2f\bigg)\biggr\}\tag{10}
\end{align*}
これで実部と虚部できれいに分かれたと思います。
もちろん、この(10)式が恒等的に成り立つのであれば、左辺・右辺の実部虚部でそれぞれ成り立つことになります。
(10)式の虚部
まずは、虚部から見ていきましょう。
虚部の虚数\(i\)は不要なので消しておくとして、両辺を\(\hbar\)で割っておきます。
そうすると、
\frac{\partial f}{\partial t}=-\frac{\hbar^2}{2m}\bigg(\big(\nabla^2\theta\big)f+2\big(\nabla\theta\big)\cdot\nabla f\bigg)\tag{11}
\end{align*}
となります。
これを意味しているのかというと、\(f\)の時間発展の方程式です。
\(f\)が何かというと、(6)式で\(f(\boldsymbol{r},t)=\sqrt{n(\boldsymbol{r},t)}\)とおいたときの、粒子数密度に関係付けられたものですよね。
だから、\(f^2=n\)は粒子数密度のことです。
そういえば、前回の記事で粒子数密度の時間変化の方程式を導きました。
それが、「連続の式」です。
量子流体の連続の式
連続の式
\begin{align*}
\frac{\partial n}{\partial t}+\nabla\cdot\big(n\boldsymbol{v})=0
\end{align*}速度場
\begin{align*}
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta
\end{align*}前回の記事はこちら
ということは(11)式は、連続の式になっていないといけないですよね。
これに関して、別途記事を書きます・・・
(10)式の実部
(10)式の虚部は連続の式に対応することがわかりました。
では、次に実部を書いていきましょう。
-\hbar \frac{\partial \theta}{\partial t}=-\frac{\hbar^2}{2mf}\nabla^2f+\frac{\hbar^2}{2m}\nabla\big(\theta\big)^2+V_{ex}+g|f|^2
\end{align*}
ここで、速度場が\(\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\)であることを使うと、
-\hbar \frac{\partial \theta}{\partial t}=-\frac{\hbar^2}{2mf}\nabla^2f+\frac{1}{2}m1\boldsymbol{v}^2+V_{ex}+g|f|^2\tag{12}
\end{align*}
となります。
この(12)式は、位相の時間変化の方程式を意味しています。
位相の時間変化と言われてもよくわからない・・・
ということで、速度場が\(\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\)であるので、(12)式にナブラ演算子\(\nabla\)を作用させて、速度場の時間変化を表す式に変えます。
-\hbar \frac{\partial \nabla \theta}{\partial t}=\nabla\bigg(-\frac{\hbar^2}{2mf}\nabla^2f+\frac{1}{2}m1\boldsymbol{v}^2+V_{ex}+g|f|^2\bigg)\tag{13}
\end{align*}
はい、ナブラ演算子\(\nabla\)を作用させただけです。
さらに、\(\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\)を使うと・・・・
m\frac{\partial \boldsymbol{v}}{\partial t}=-\nabla\bigg(-\frac{\hbar^2}{2mf}\nabla^2f+\frac{1}{2}m\boldsymbol{v}^2+V_{ex}+g|f|^2\bigg)\tag{14}
\end{align*}
となります。
運動方程式が出てきました!!
さらに、(14)式の両辺を\(m\)で割り、粒子数密度に関係した\(f(\boldsymbol{r},t)=\sqrt{n(\boldsymbol{r},t)}\)ということを使うと、
m\frac{\partial \boldsymbol{v}}{\partial t}=-\nabla \bigg(\tilde{\mu}+\frac{m\boldsymbol{v}^2}{2}\bigg)\tag{15}
\end{align*}
ここで、\(\tilde{\mu}=V_{ex}+ng–\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\)とおきました。
\frac{\partial \boldsymbol{v}}{\partial t}=-\frac{1}{m}g\nabla n-\nabla\bigg(\frac{1}{2}\boldsymbol{v}^2\bigg)-\frac{1}{m}\nabla V_{ex}+\nabla\bigg(-\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{15}
\end{align*}
となります。
さて、もうほとんど流体力学のオイラー方程式になっています。
ギブス・ディエムの式を使う
唐突になってしまいますが、熱力学の示強変数(\(T,p,\mu\))の変化に対してギブス・ディエムの式というのがあります。
SdT-Vdp+Nd\mu=0\tag{16}
\end{align*}
・粒子数\(N\)
・化学ポテンシャル\(\mu\)
これを用いることにより、(15)式の右辺第一項の式が、以下のように変わるというのを本項で見ていきます。
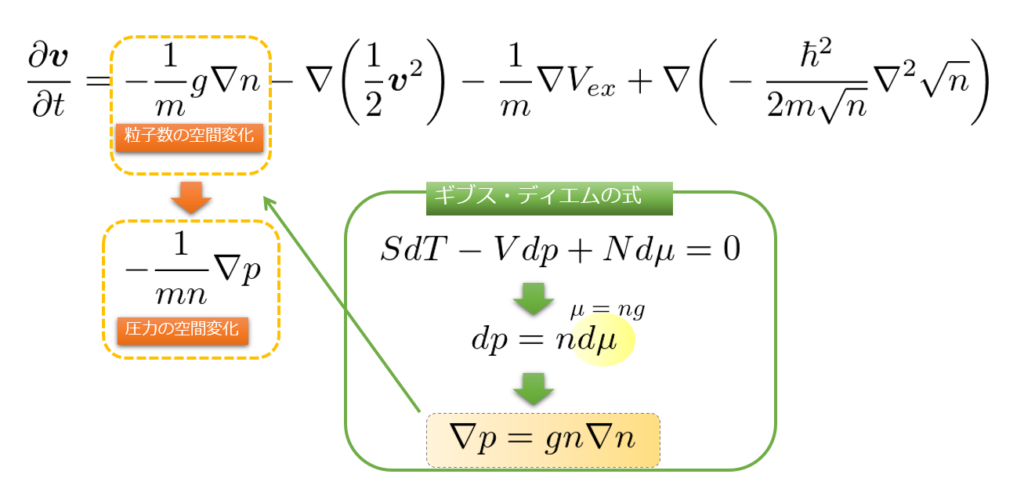
絶対零度近傍なので温度変化は考えない
今考えている量子流体は、絶対零度のボース・アインシュタイン凝縮を起こした系を考えているので、温度の変化を考えなくても良いのですね。
ですので、ギブス・ディエムの式の\(dT=0\)とすると、
dp=nd\mu=0\tag{17}
\end{align*}
※粒子数密度\(n=\frac{N}{V}\)
ここで、化学ポテンシャル\(\mu\)は主に何が担っているのかを考えます。
化学ポテンシャルは、粒子数が変化したことによる何かしらの手ごたえをポテンシャルと表現しているということです(wikipedia:化学ポテンシャル)。
粒子数に関係したなにかしらのポテンシャルということなのですが、以下に
\tilde{\mu}=V_{ex}+ng-\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\tag{18}
\end{align*}
と置いた時の量ということです。
バルクで考える
ただ、捕獲ポテンシャルの端(ポテンシャルが高い領域)でものごとを議論することはしないですよね。
捕獲ポテンシャルはボース粒子を捕獲するためのポテンシャルなので・・・・・
だから、捕獲ポテンシャルによる外力がはたらかない真ん中近傍でどうなのかというのを考えることにすると・・・・
そこはバルクと呼ばれています。
これは、粒子数変化も特に大きい変化もないような領域を考えていることに相当します。

ということは、粒子数に関係したポテンシャルのうちで、相互作用項\(ng\)のみがかなり支配的であるということになります。
相互作用項は、2粒子間の相互作用を考えるので\({}_N C _2=\frac{N(N-1)}{2}\sim N^2\)と\(N^2\)のオーダーということになるので、相互作用項が支配的であることがわかるかと思います。
そう考えると、ギブス・ディエムの式より、
dp&=nd(ng)\\
dp&=ngdn&\tag{19}
\end{align*}
時間変化よりも空間変化の寄与の方が大きいとすると、
\nabla p=ng\nabla n\tag{20}
\end{align*}
となります。
よって、(15)式は、
\frac{\partial \boldsymbol{v}}{\partial t}=-\frac{1}{mn}\nabla p-\nabla\bigg(\frac{1}{2}\boldsymbol{v}^2\bigg)-\frac{1}{m}\nabla V_{ex}+\nabla\bigg(-\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{21}
\end{align*}
となります(^^)/
はい、量子流体のオイラー方程式の完成!!
おまけ
(21)式でも良いのですが、おまけです。
ベクトル解析で、2つのベクトル\(\boldsymbol{A}\)、\(\boldsymbol{B}\)にたいして
\nabla(\boldsymbol{A}\cdot\boldsymbol{B})=(\boldsymbol{B}\cdot\nabla)\boldsymbol{A}+(\boldsymbol{A}\cdot\nabla)\boldsymbol{B}+\boldsymbol{A}\times(\nabla\times\boldsymbol{B})+\boldsymbol{B}\times(\nabla\times\boldsymbol{A})\tag{22}
\end{align*}
という公式があります。
これを使って、\(\boldsymbol{A}=\boldsymbol{B}=\boldsymbol{v}\)とすると、
\nabla\bigg(\frac{\boldsymbol{v}^2}{2}\bigg)=(\boldsymbol{v}\cdot\nabla)\boldsymbol{v}+\boldsymbol{v}\times(\nabla\times\boldsymbol{v})\tag{23}
\end{align*}
となります。
前回の記事で示したように、量子流体で位相\(\theta(\boldsymbol{r},t)\)に特異点がない場合は、(23)式の\(\nabla\times \boldsymbol{v}=0\)となります。
よって、
\nabla\bigg(\frac{\boldsymbol{v}^2}{2}\bigg)=(\boldsymbol{v}\cdot\nabla)\boldsymbol{v}\tag{24}
\end{align*}
これを使えば、(21)式は下記のように書くこともできます。
\frac{\partial \boldsymbol{v}}{\partial t}+\frac{1}{mn}=\nabla p-(\boldsymbol{v}\cdot\nabla)\boldsymbol{v}-\frac{1}{m}\nabla V_{ex}+\nabla\bigg(-\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{25}
\end{align*}
通常の流体と量子流体は何が違うのか?
最後に、通常の流体力学の方程式(ナビエストークス方程式)と今回導出した量子流体のオイラー方程式とを見比べてみましょう。
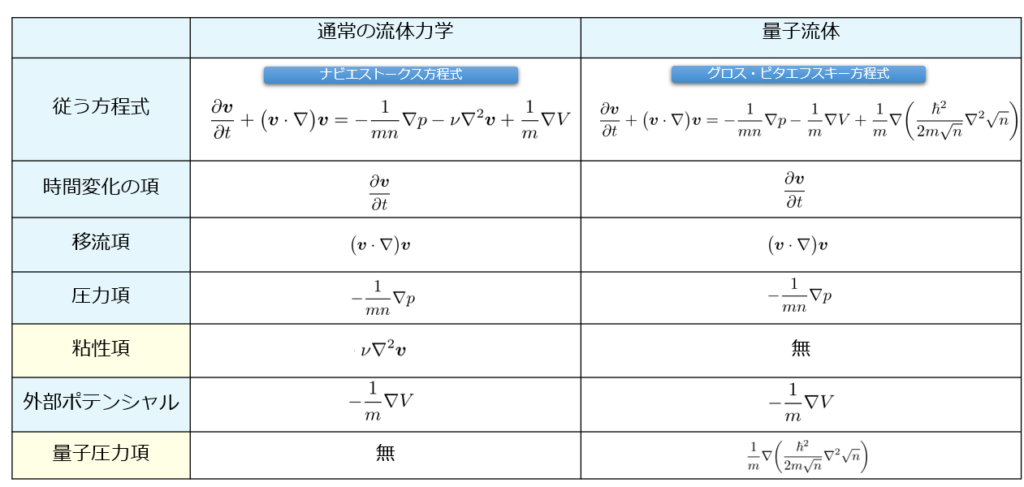
通常の流体力学と量子流体の違いは以下の2点であることがわかります。
- 量子流体には粘性が無い
- 量子流体には量子圧力項が存在する
まとめ
本記事では、低温状態で出現するボース・アインシュタイ凝縮体(特に希薄原子気体)が従う方程式であるGP方程式を式変形して、流体力学のオイラー方程式のような式を導出しました。
グロス・ピタエフスキー方程式(略してGP方程式)
\begin{align*}
i\hbar\frac{\partial \psi(\boldsymbol{r},t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r},t)+V_{ex}\psi(\boldsymbol{r},t)+g|\psi(\boldsymbol{r},t)|^2\psi(\boldsymbol{r},t)\tag{1}
\end{align*}オイラー方程式(量子流体バージョン)
\begin{align*}
\frac{\partial \boldsymbol{v}}{\partial t}+\big(\boldsymbol{v}\cdot\nabla\big)\boldsymbol{v}=-\frac{1}{mn}\nabla p-\frac{1}{m}\nabla V+\frac{1}{m}\nabla\bigg(\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{25}
\end{align*}
もしくは、\begin{align*}
\frac{\partial \boldsymbol{v}}{\partial t}=-\frac{1}{mn}\nabla p-\nabla\bigg(\frac{\boldsymbol{v}^2}{2}\bigg)-\frac{1}{m}\nabla V+\frac{1}{m}\nabla\bigg(\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{21}
\end{align*}
(2)(3)式のような流体力学の「オイラー方程式」ととてもよく似ている!!