どうも(^^)/
本記事では、量子力学的効果によって出現する量子流体についてのお話をしたいと思います。
- ボース粒子、フェルミ粒子の特徴について
- ボース・アインシュタイン凝縮
これらの内容を本格的に学ぼうと思うと、主に統計力学と量子力学の知識が必要になってきます。
しかし、本記事ではできるだけイメージをわかりやすく解説し、量子流体とはどういった物理を対象にしているのかを理解してもらうことを目的としておきます(^^)
ですので、難しい数式は出てきません(^^)/
以下、本記事の内容で重要となる用語を列挙しておきます♪
区別できない粒子には、フェルミ粒子とボース粒子というのがあります。
今回は特に、ボース粒子が非常に重要になります。
ボースアインシュタイン凝縮
量子流体が出現する舞台となるのは、低温状態で出現するボースアインシュタイン凝縮という現象が重要です。
前半はとてもやさしく、後半は物理の用語を少し使いながら易しく解説したいと思います。
同種粒子とは
量子力学というと、光、あるいは原子や素粒子などの小さな粒子を対象にした理論であり、ニュートン力学では記述することのできない現象を取り扱うときに使いますよね。
しかし、量子力学は系が小さいというだけではなく、温度が非常に小さい場合においてもその効果を発揮するのです。
その時に肝となる考え方は、「同種粒子は区別しない」ということです。
同種粒子は区別しないというのはどういうことかというのを簡単に説明しておきましょう。
まずは粒子を区別できる状態と区別できない状態だと何が起こるかというのを見ましょう。
同種粒子からフェルミ粒子とボース粒子を理解する
まずは、フェルミ粒子とボース粒子の特徴を理解することからはじめましょう!
2つの粒子を用意し、その2つの粒子を2つの部屋に入れるというのを考えます。
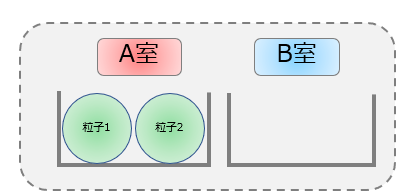
丸の絵が粒子で、部屋が物理の言葉で言うならエネルギー準位だと考えてください。
それぞれを粒子1、粒子2と名付けておきます。
この時点では、粒子を1と粒子2とで名付けているので、思いっきり粒子を区別していますよね・・・・
以下考えるのは、その2つの粒子を2つの箱に入れるのは何通りあるのか?というのを考えるです。
粒子が区別できる場合:マクスウェル・ボルツマン分布
粒子が区別できる場合は、以下のように4通りのパターンが存在します。
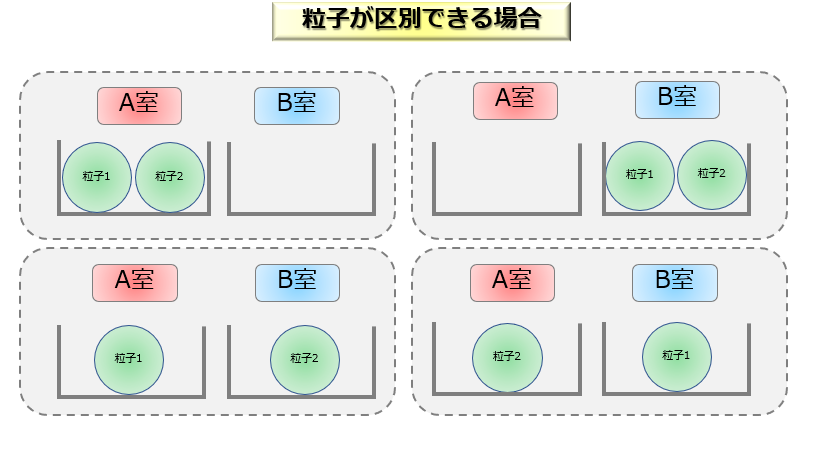
これが、マクスウェル・ボルツマン分布に従う考え方で、高温状態であるときにはこの考え方で良いのです。
これは、粒子には番号付でちゃんと区別しているので個性があると考えているのです。
しかし、以下で見るように低温状態であると粒子の個性が消え、粒子が区別できない同種粒子であると考え方が肝になってきます。
粒子が区別できない場合
粒子が区別できないという事実から、粒子を部屋に入れるルールは以下の2つに分けられます。
- どの部屋にも粒子は1つしか所有できない:フェルミ粒子
もしくは・・・
- どの部屋にも粒子を何個も所有できる:ボース粒子
どの部屋にも粒子は1つしか所有できない:フェルミ粒子
粒子が区別できる場合と違って、今回はの場合は粒子は区別できず、
さらに部屋には1個しか粒子が所有できないというルールがあるために、
4通りではなく1通りの状態しかないということになります。
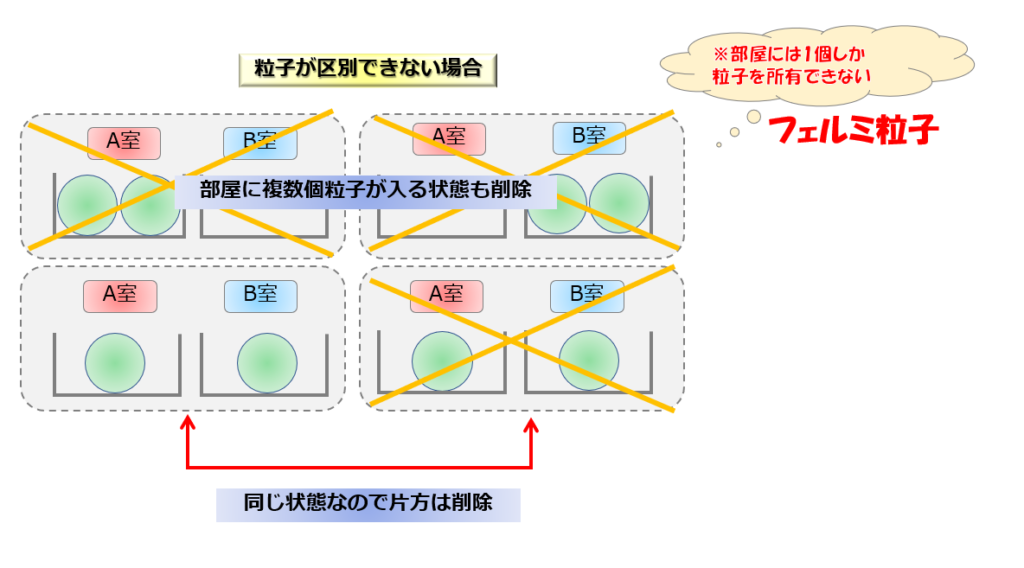
部屋には1個しか粒子が所有できないというルールのことを、パウリの排他律といいます。
粒子は区別できず、さらに部屋には1個しか粒子が所有できないという数え方をする粒子のことをフェルミ粒子といいます。
どの部屋にも粒子を何個も所有できる:ボース粒子
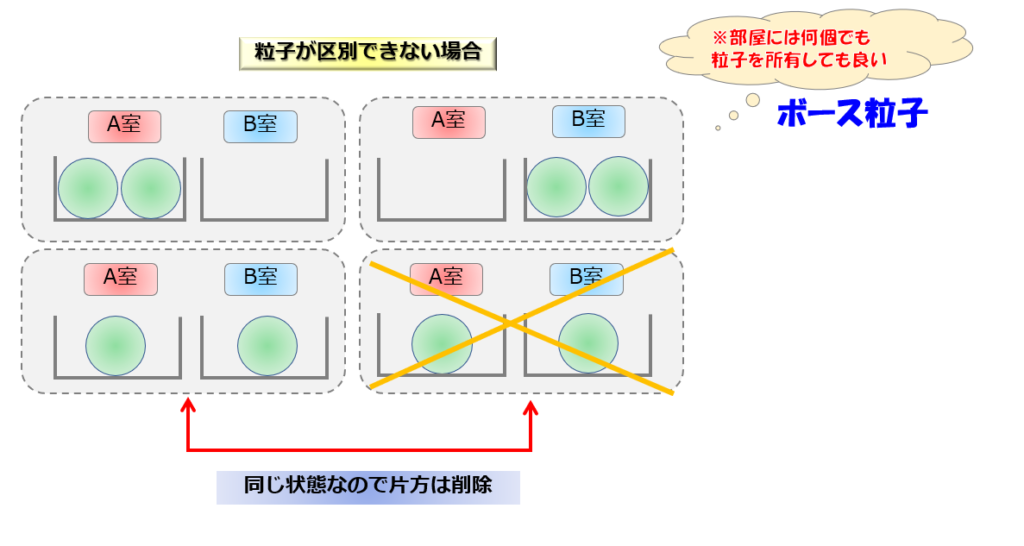
粒子が区別できる場合と違って、今回はの場合は、粒子は区別できず、しかし部屋には何個でも粒子を所有しても良いルールにします。
この場合は、4通りではなく3通りの状態しかないということになります。
同種粒子は粒子の入れ替えに対して対称である
フェルミ粒子もボース粒子が区別できないという事実から導き出された粒子です。
特に、低温状態で顕著に出て、量子力学的な効果によって粒子は区別できないということを意味しています。
言い換えると、これらの区別できない同種粒子は、粒子の入れ替えに対して対称であるという言い方をします。
粒子って2種類しかないのか?
電子とか陽子とか中性子とかは粒子だと思っているのに・・・・
と思う人もいるので、強調しておきます。
電子とか陽子とか中性子などが、この後詳しく説明する「フェルミ粒子かボース粒子のどちらかの性質に分類される」という大枠を今話したことになります。
以下、例を少し挙げておきます。
前半戦の終了です(‘ω’)ノ
前半の内容で、フェルミ粒子とボース粒子の特徴を何となくでも理解できたと思いますので、
後半は、さきほどの、2種類の粒子を部屋に粒子を入れる操作を頭に描きながら、フェルミ粒子とボース粒子について少し物理用語も使いながら解説をしたいと思います(^^)/
フェルミ粒子とボース粒子が顕著に違いが出るのは低温状態
同種粒子は粒子の区別をしないということがとても重要であるという話をしました。
同種粒子は粒子の区別しないということから、フェルミ粒子とボース粒子という全く性質の異なる粒子に分類できるという説明をしましたよね。
大事なポイントは以下2点です。
- 区別できない粒子は、「2種類」の粒子(フェルミ粒子、ボース粒子)がある
- フェルミ粒子とボース粒子の違いは低温状態で性質が大きく異なる
この2点がすごく大事です。
つまり、フェルミ粒子とボース粒子は高温状態なら特に特徴の違いは出てこないということなのです。
もちろん、先ほどのフェルミ粒子とボース粒子は各々全然違う特徴であることをお話しましたが、高温状態ならその特徴はほとんど消えています。
フェルミ粒子とボース粒子の違いがはっきりと出てくるのは、特に低温状態であるということを覚えておいてください(‘ω’)ノ
では、フェルミ粒子とボース粒子をそれぞれ詳しく見ていきます。
フェルミ粒子:1つのエネルギー準位にひとつの状態しか入れない
ここでは、粒子間の相互作用がないような理想的なフェルミ粒子を考えます。
例えば、以下のようなエネルギー準位を考えましょう。
※一応量子力学ではエネルギー準位がとびとびであることを前提に絵を書いています。
エネルギー準位が高いよりも低い方が安定であるために、下の方から粒子が埋められていくということになります。
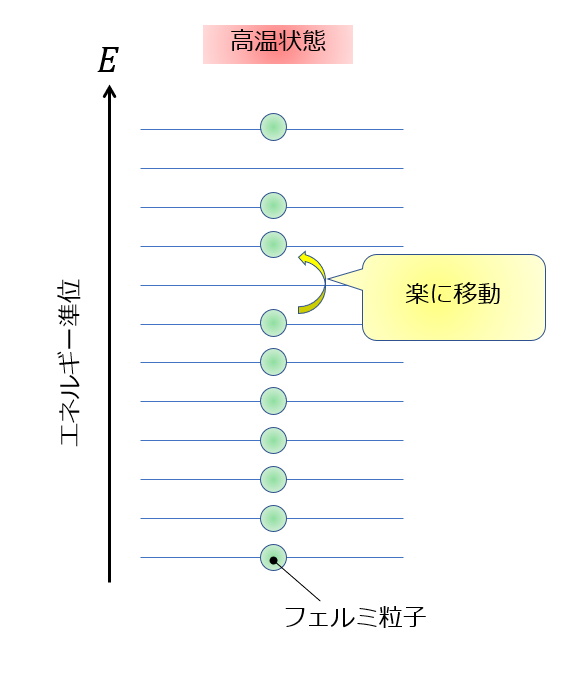
しかし、フェルミ粒子の場合はこのときに、強い制約があるのでしたよね。
それは、1つのエネルギー準位にはひとつの粒子状態しか入ることができないという制約です。
これをパウリの排他律ということを説明しました。
高温状態であれば、粒子がエネルギー準位を1つ超えるのは簡単で、必ずしも下から順番に埋め尽くされていくというわけではありません・・・
もちろんエネルギー準位の下から粒子を埋めていった方がエネルギーが低く安定ですが、高温状態の粒子からしたら、「1つのエネルギー準位なんて大した山の高さじゃないぜ!!」って思っているのですよ(‘ω’)たぶん・・・
補足説明
※1つの粒子と書かずに、1つの粒子状態と書いたのには理由があります。
例えば、エネルギー準位状態が同じでも、状態が異なる場合というのが存在します。
これを縮退といいます。
縮退:同じエネルギー準位だけど、状態が異なる。
簡単な例で言うと、電子のスピンなどは、同じエネルギー準位であったとして、アップスピン、ダウンスピンと状態が異なるものが存在します。
つまり、絵で書くと・・・
これは一見粒子が同じエネルギー準位に所有されているように見えますが、フェルミ粒子の制約は「同じエネルギー準位に同じ状態を所有できない」ということなので、上の絵のような状態はありなのですよね。
つまり、正確には同じエネルギー準位に同じ粒子を所有的ないという意味ではなく、同じ状態を所有できないということを意味なのです。
では、低温状態になると、基本的に粒子状態は下から埋めていくことになるので、下記のようになります。
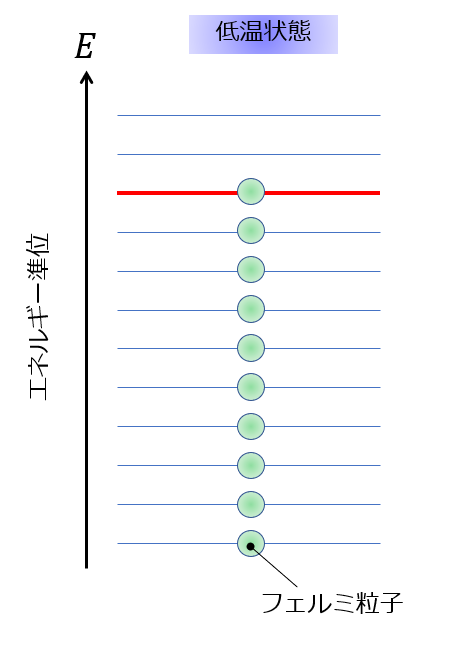
フェルミ粒子に関しては、これ以上深堀した話はしません(‘ω’)ノ
ボース粒子:1つのエネルギー準位に何個でも粒子を所有できる
ここでは、粒子間に相互作用がないような理想的なボース粒子を考えます。
フェルミ粒子にはパウリの排他律のように、各エネルギー準位に所有できる粒子状態に制限があった(1つの状態だけ)のですが、ボース粒子にはその制限がありません。
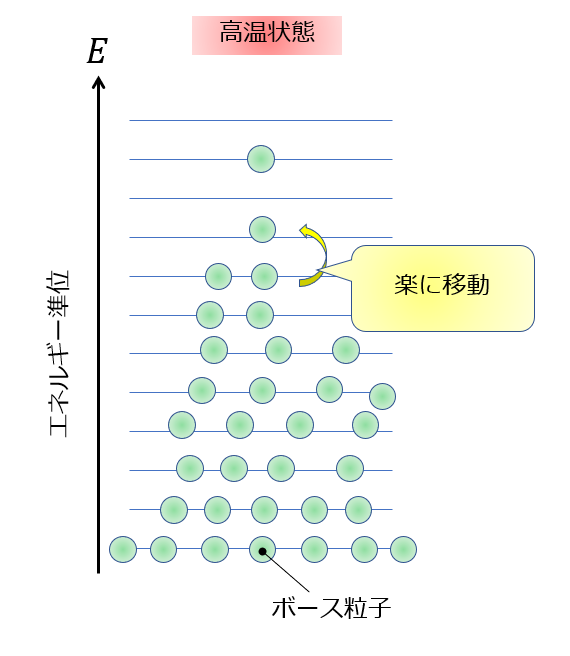
ボース粒子は、そのおかげで低温状態になったときに、その効果を発揮することになります。
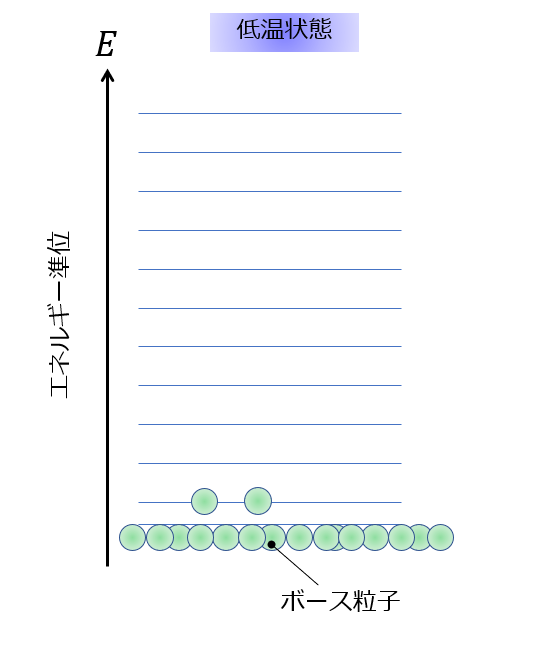
低温状態では、大多数の粒子が最低エネルギー準位に落ち込むということが起こるのです。
これがボースアインシュタイン凝縮と呼ばれるものです。
これは何を意味しているのでそうか・・・
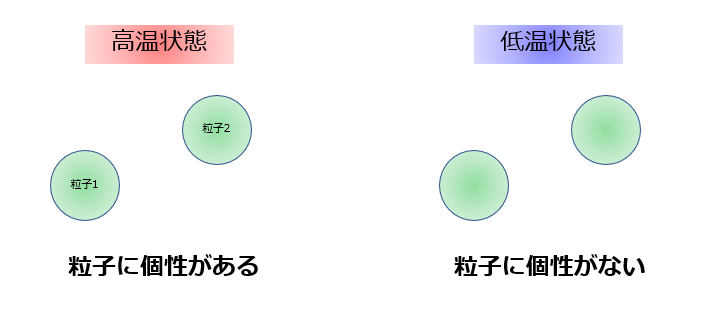
高温状態であれば、どのエネルギー準位も行き放題で色んな粒子状態を眺めても色々な状態をとっているということになります。
つまり、これは粒子の個性があるということを意味しています。
逆に低温状態にすると、大多数が同じ(最低)エネルギー準位に落ち込むため、個性がなくなってしまうということになります。
- 高温状態:粒子に個性がある
- 低温状態:粒子の個性がなくなる
ド・ブロイ波長
粒子が波の性質をもつとすると、
\lambda=\frac{h}{p}
\end{align*}
\(p\):運動量
\(h\):プランク定数
ということを提案しました。
ここで、古典力学の考え方として、理想気体の場合は気体分子運動論に従って粒子は運動すると考えます。
そうすると、粒子の運動エネルギーの平気値が、熱的な温度と等価であるということを導けますよね。
\frac{mv^2}{2}=\frac{3}{2}k_{B}T
\end{align*}
ここに、運動量\(p\)を導入して、運動エネルギーを\(\frac{p^2}{2m}\)と書くと、
\frac{p^2}{2m}=\frac{3}{2}k_{B}T
\end{align*}
ここで、\(p=\frac{h}{\lambda}\)を用いると、
\lambda=\frac{h}{\sqrt{3mk_{B}T}}
\end{align*}
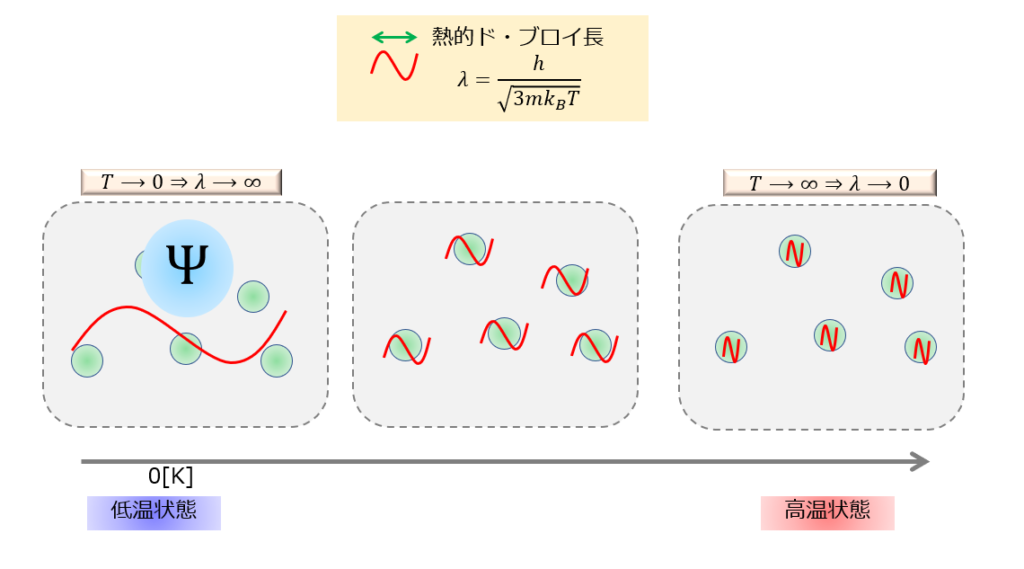
これが熱的ド・ブロイ波長と呼ばれています。
※分母に3という数字がありますが、これは次元が3次元であることから来ているので、特に3ということに本質的な意味はありません。
これは個々の粒子を波として表現した場合の波長であります。
つまり、
高温状態(\(T\rightarrow \infty\))
\lambda=\frac{h}{\sqrt{3mk_{B}T}}\rightarrow 0
\end{align*}
低温状態(\(T\rightarrow 0\))
\lambda=\frac{h}{\sqrt{3mk_{B}T}}\rightarrow \infty
\end{align*}
このように、高温状態では粒子の波を性質が見えなくなり、逆に低温状態では波の性質が際立つのか・・
というのがわかるのです。
先ほどは、低温状態にすると、
- 最低のエネルギー準位に大多数の粒子状態を所有することになる
- 粒子の個性が消える
- 大多数の粒子がひとつの状態で記述することができる
というのをマンガ絵で理解しやすいように表現してみます。
低温にすると大多数の粒子が同じ状態に落ち込むため、粒子の個性というのが消えて大多数の粒子が同じ状態であるために、1つの波動関数\(\psi\)で記述できるようになるということです。
これがボース・アインシュタイ凝縮であり、量子流体の舞台となるわけです。
言い換えると、これが低温状態で出現する量子力学的による波(流体)の性質を持った量子流体というわけです。
まとめ
今回は、量子流体というのが何かというのを説明するために、フェルミ粒子とボース粒子の特徴を簡単に説明しました。
- フェルミ粒子:1つのエネルギー準位に1つの粒子状態しか所有できない(パウリの排他律)
- ボース粒子:1つのエネルギー準位に複数の粒子状態を所有できる
本記事で学んだ重要なことは以下の事です。
ボース粒子は、低温状態で大多数の粒子が最低エネルギー準位に落ち込むボース・アインシュタイ凝縮という現象があります
- 最低のエネルギー準位に大多数の粒子状態を所有することになる
- 粒子の個性が消える
- 大多数の粒子がひとつの状態\(\psi\)で記述することができる
低温状態で出現する量子力学的による波(流体)の性質を持った流体を量子流体といいます。













バリバリ優秀な方ですね。
ボース粒子の説明について書かせて頂きます。
「粒子を区別しないで考えた事象(場合)は等確率で現れる」と考えると矛盾が生じてしまいます。(コルモゴロフの確率の公理3に反してしまいます。)
4つの量子状態間を移動している2個のボース粒子を考えます。
2つの量子状態をaグループ、残りの2つの量子状態をbグループとして次の事象の現れる確率を考えてください。
Ⅰ:2個ともaグループ内にある
Ⅱ:1個がaグループ内、1個がbグループ内にある
Ⅲ:2個ともbグループ内にある
コメントいただきましてありがとうございます。
「粒子を区別しないで考えた事象(場合)は等確率で現れる」という部分に関して、そこからどのような矛盾があるのか具体的にはわかりませんが、
箱に振り分けるという考え方をするとわかりにくいかもしれませんね。
確率については少々議論が難しくなりますが、統計力学でのスタートが取りうる状態の数と考えると、場合の数を数えることに注力してみます。
状態a、状態bという二つの状態があり、区別できる場合と区別できない場合で考えると違いが明確かと思います。
|を用意して
・|より右側の状態をa状態、
・|より左側をb状態とします。
ここで、取りうる状態は
①② |の並べ替えになります。
【区別できる場合】
①② |
①も②も|の右か左かを選べるので
W = 2C1 *2C1 = 4通り
①② |
|①②
①|②
② |①
【区別できない場合】
①と②は区別できないので、〇とします。
〇〇 |
を並べ替える3!通りに対して〇が区別できないから2!で割る。
W = (2+1)!/(2!*1!) = 3! = 3通り
〇〇 |
|〇〇
〇|〇
区別できない場合に関して一般化すると、粒子N個、状態がM個である場合、
〇〇〇・・・〇 |||・・・|||
※〇がN個、|がM-1個
これらを並べ替える、(N+M-1)!通りに対して区別できない〇の分のN!と|の分の(M-1)!で割ると取りうる場合の数は、
W = (N+M-1)!/(N)!/(M-1)!
これは箱に粒子を詰める場合と考え方が異なるので、上記のように考えました。
ミクロカノニカルでの等確率とは、ある幅ΔEの間はエネルギーが等しいと考えるため|||・・・|||のどの部分にも〇は等しく振り分けることができると(仮定)言っているだけだと理解しています。
korokoro 様
(N+M-1)!/(N)!/(M-1)!通りの粒子配置が等確率で現れるのは実験結果に基づいていて疑いようのないことです。
問題なのは
「粒子を区別しないで考えた事象(場合)は等確率で現れる」という説明の仕方です。
Ⅰ:2個ともaグループ内にある
Ⅱ:1個がaグループ内、1個がbグループ内にある
Ⅲ:2個ともbグループ内にある
という3通りの事象が等確率で現れるとすれば、Ⅰ,Ⅱ,Ⅲの現れる確率の比は1:2:1です。korokoro様の書かれたとおり4つの量子状態を考えると10通りの事象が考えられます。それらが等確率で現れるとすればⅠ,Ⅱ,Ⅲの現れる確率の比は3:4:3です。
(N+M-1)!/(N)!/(M-1)!通りの粒子配置が等確率で現れるのは量子状態に所属する粒子のうち1個しか他の量子状態に移動できない(メスシリンダーのように)からだと考えると説明できます。
以下のモデルはEXCELのマクロです。器3,ボール3のシミュレーションです。
マクロ名を適当につけてSubマクロ名()とEnd Subの間に貼り付けてください。
B3,C3,D3に初期配置例えば3,0,0をB5に移動回数例えば1000000を入力します。
マクロを実行します。
各配置arrangementの現れる時間time[min]が出力されます。
ご自分でその比を出してみてください。
シリンダーモデルでは 全ての配置が等確率で現れるのが判ります。
皿モデル
Dim Time(4, 4, 4): Dim K(4)
40 Cells(1, 1) = “3 plates”: Cells(1, 2) = “3 balls”
50 Cells(7, 1) = “arrangement”: Cells(7, 2) = “time[min]”
60 Time(3, 0, 0) = 0: Time(2, 1, 0) = 0: Time(2, 0, 1) = 0
70 Time(1, 2, 0) = 0: Time(1, 1, 1) = 0: Time(1, 0, 2) = 0
80 Time(0, 3, 0) = 0: Time(0, 2, 1) = 0: Time(0, 1, 2) = 0
90 Time(0, 0, 3) = 0
100 G = 3
110 Mov = Val(Cells(5, 2))
120 M = 0: N = 0
130 K(1) = Cells(3, 2): N = N + K(1)
140 K(2) = Cells(3, 3): N = N + K(2)
150 K(3) = Cells(3, 4): N = N + K(3)
160 RD = Int(Rnd * 1000)
170 r = RD – Int(RD / N) * N + 1: P = 0: J = 0
180 J = J + 1: P = P + K(J)
190 If r > P Then GoTo 180
200 JS = J
210 Time(K(1), K(2), K(3)) = Time(K(1), K(2), K(3)) + 1 / N
220 K(J) = K(J) – 1
230 SD = Int(Rnd * 1000)
240 S = SD – Int(SD / (G – 1)) * (G – 1) + 1
260 If S < JS Then K(S) = K(S) + 1: GoTo 310
270 S = S + 1: K(S) = K(S) + 1
310 M = M + 1
320 If M 0 Then A(I) = J: I = I + 1
190 Next J
200 RD = Int(Rnd * 1000)
210 r = RD – Int(RD / I) * I
220 Time(K(1), K(2), K(3)) = Time(K(1), K(2), K(3)) + 1 / I
230 K(A(r)) = K(A(r)) – 1
240 SD = Int(Rnd * 1000)
250 S = SD – Int(SD / (G – 1)) * (G – 1) + 1
260 If S < A(r) Then K(S) = K(S) + 1: GoTo 280
270 S = S + 1: K(S) = K(S) + 1
280 For J = 0 To I
290 A(J) = 0
300 Next J
310 M = M + 1
320 If M < Mov Then GoTo 160
330 Cells(8, 1) = "(3,0,0)": Cells(8, 2) = Time(3, 0, 0)
340 Cells(9, 1) = "(2,1,0)": Cells(9, 2) = Time(2, 1, 0)
350 Cells(10, 1) = "(2,0,1)": Cells(10, 2) = Time(2, 0, 1)
360 Cells(11, 1) = "(1,2,0)": Cells(11, 2) = Time(1, 2, 0)
370 Cells(12, 1) = "(1,1,1)": Cells(12, 2) = Time(1, 1, 1)
380 Cells(13, 1) = "(1,0,2)": Cells(13, 2) = Time(1, 0, 2)
390 Cells(14, 1) = "(0,3,0)": Cells(14, 2) = Time(0, 3, 0)
400 Cells(15, 1) = "(0,2,1)": Cells(15, 2) = Time(0, 2, 1)
410 Cells(16, 1) = "(0,1,2)": Cells(16, 2) = Time(0, 1, 2)
420 Cells(17, 1) = "(0,0,3)": Cells(17, 2) = Time(0, 0, 3)
korokoro 様
申し訳ありません。マクロがうまく送れませんでした。
皿モデル
Dim Time(4, 4, 4): Dim K(4)
40 Cells(1, 1) = “3 plates”: Cells(1, 2) = “3 balls”
50 Cells(7, 1) = “arrangement”: Cells(7, 2) = “time[min]”
60 Time(3, 0, 0) = 0: Time(2, 1, 0) = 0: Time(2, 0, 1) = 0
70 Time(1, 2, 0) = 0: Time(1, 1, 1) = 0: Time(1, 0, 2) = 0
80 Time(0, 3, 0) = 0: Time(0, 2, 1) = 0: Time(0, 1, 2) = 0
90 Time(0, 0, 3) = 0
100 G = 3
110 Mov = Val(Cells(5, 2))
120 M = 0: N = 0
130 K(1) = Cells(3, 2): N = N + K(1)
140 K(2) = Cells(3, 3): N = N + K(2)
150 K(3) = Cells(3, 4): N = N + K(3)
160 RD = Int(Rnd * 1000)
170 r = RD – Int(RD / N) * N + 1: P = 0: J = 0
180 J = J + 1: P = P + K(J)
190 If r > P Then GoTo 180
200 JS = J
210 Time(K(1), K(2), K(3)) = Time(K(1), K(2), K(3)) + 1 / N
220 K(J) = K(J) – 1
230 SD = Int(Rnd * 1000)
240 S = SD – Int(SD / (G – 1)) * (G – 1) + 1
260 If S < JS Then K(S) = K(S) + 1: GoTo 310
270 S = S + 1: K(S) = K(S) + 1
310 M = M + 1
320 If M < Mov Then GoTo 160
330 Cells(8, 1) = "(3,0,0)": Cells(8, 2) = Time(3, 0, 0)
340 Cells(9, 1) = "(2,1,0)": Cells(9, 2) = Time(2, 1, 0)
350 Cells(10, 1) = "(2,0,1)": Cells(10, 2) = Time(2, 0, 1)
360 Cells(11, 1) = "(1,2,0)": Cells(11, 2) = Time(1, 2, 0)
370 Cells(12, 1) = "(1,1,1)": Cells(12, 2) = Time(1, 1, 1)
380 Cells(13, 1) = "(1,0,2)": Cells(13, 2) = Time(1, 0, 2)
390 Cells(14, 1) = "(0,3,0)": Cells(14, 2) = Time(0, 3, 0)
400 Cells(15, 1) = "(0,2,1)": Cells(15, 2) = Time(0, 2, 1)
410 Cells(16, 1) = "(0,1,2)": Cells(16, 2) = Time(0, 1, 2)
420 Cells(17, 1) = "(0,0,3)": Cells(17, 2) = Time(0, 0, 3)
korokoro 様
シリンダーモデル
Dim A(4): Dim Time(4, 4, 4): Dim K(4)
30 Cells(1, 1) = “3 cylinders”: Cells(1, 2) = “3 balls”
40 Cells(7, 1) = “arrangement”: Cells(7, 2) = “time[min]”
50 A(1) = 0: A(2) = 0: A(3) = 0
60 Time(3, 0, 0) = 0: Time(2, 1, 0) = 0: Time(2, 0, 1) = 0
70 Time(1, 2, 0) = 0: Time(1, 1, 1) = 0: Time(1, 0, 2) = 0
80 Time(0, 3, 0) = 0: Time(0, 2, 1) = 0: Time(0, 1, 2) = 0
90 Time(0, 0, 3) = 0
100 G = 3
110 Mov = Val(Cells(5, 2))
120 M = 0: N = 0
130 K(1) = Cells(3, 2): N = N + K(1)
140 K(2) = Cells(3, 3): N = N + K(2)
150 K(3) = Cells(3, 4): N = N + K(3)
160 I = 0
170 For J = 1 To G
180 If K(J) > 0 Then A(I) = J: I = I + 1
190 Next J
200 RD = Int(Rnd * 1000)
210 r = RD – Int(RD / I) * I
220 Time(K(1), K(2), K(3)) = Time(K(1), K(2), K(3)) + 1 / I
230 K(A(r)) = K(A(r)) – 1
240 SD = Int(Rnd * 1000)
250 S = SD – Int(SD / (G – 1)) * (G – 1) + 1
260 If S < A(r) Then K(S) = K(S) + 1: GoTo 280
270 S = S + 1: K(S) = K(S) + 1
280 For J = 0 To I
290 A(J) = 0
300 Next J
310 M = M + 1
320 If M < Mov Then GoTo 160
330 Cells(8, 1) = "(3,0,0)": Cells(8, 2) = Time(3, 0, 0)
340 Cells(9, 1) = "(2,1,0)": Cells(9, 2) = Time(2, 1, 0)
350 Cells(10, 1) = "(2,0,1)": Cells(10, 2) = Time(2, 0, 1)
360 Cells(11, 1) = "(1,2,0)": Cells(11, 2) = Time(1, 2, 0)
370 Cells(12, 1) = "(1,1,1)": Cells(12, 2) = Time(1, 1, 1)
380 Cells(13, 1) = "(1,0,2)": Cells(13, 2) = Time(1, 0, 2)
390 Cells(14, 1) = "(0,3,0)": Cells(14, 2) = Time(0, 3, 0)
400 Cells(15, 1) = "(0,2,1)": Cells(15, 2) = Time(0, 2, 1)
410 Cells(16, 1) = "(0,1,2)": Cells(16, 2) = Time(0, 1, 2)
420 Cells(17, 1) = "(0,0,3)": Cells(17, 2) = Time(0, 0, 3)
korokoro 様
度々、申し訳ありません。
自分でEXCELに貼り付けたところマイナス「-」が「?」になってしまいました。「?」を半角のマイナスに変えると実行できます。
よろしくお願いいたします。