量子流体力学と古典流体力学の「似ている点・異なる点」を解説しよう！

どうも(^^)/いきなりの質問ですが、
量子流体力学というのはご存知でしょうか？
とてもマイナーな研究テーマなので、あまり聞いたことがないかもしれませんね(^^;)

本記事の内容

「量子流体」と「古典流体」の物理的な本質の違いを知ろう
「量子流体」と「古典流体」の類似性を見よう

量子流体の例を以下に列挙しておきましょう。

量子流体の例

超流動ヘリウムとは・・・
低温状態（絶対零度近傍）で、ヘリウム原子が作り出す粘性のない流体現象のことです。ヘリウムは4.2Kの温度で液体になり、2.17K以下で超流動現象を示します。
希薄原子気体ボースアインシュタイン凝縮体（希薄原子気体BEC）
1925年にアインシュタインによって理論的に予言された、1995年に希薄な中性原子気体のレーザー冷却による低温状態（絶対零度近傍）の実現によって実験で観測されたボース凝縮による粘性のない流体現象のことです。

※こちらの動画が面白いです。

これらを総称して量子流体と呼んでいます。

しかし、上述している文の中でも”流体現象”という言葉を使っていますが、皆さんが想像している流体現象とは異なっているのです。

流体現象というと、皆さんがよく目にする川の流れを想像するでしょう・・・

こんな感じ↓

しかし、量子流体は通常の流体現象（古典流体）とは異なる方程式に従い、異なる現象を示します。

通常の川の流れなどが従う流体力学のことを、量子流体と区別して古典流体力学と呼び、
超流動ヘリウムなどが従う低温状態の量子的効果によって出現する流体力学のことを、総称して量子流体力学と呼びます。（もちろん希薄原子気体BECも含みます）

これら2つの「量子流体」と「古典流体」は、同じ流体現象に見えても流体を示すための物理的背景が全く異なります。

しかし、同じ流体現象なので従う方程式が似ているという面もあり、とても面白いのです(^^)/

カマキリ

量子流体の入門を体験してみよう

これを本格的に学ぼうと思うと、量子力学と統計力学の勉強が必要になります。

そのような学問は量子統計力学と呼ばれており、学ぶのにもとても時間が必要になるでしょう。しかも、1粒子の量子力学の問題ではなくて、大多数の粒子を対象にするため多体系の量子力学を対象にしています。

この記事を読んで、「なんかわかったような気がする！！」と思ってもらえればOKです。

カマキリ

頑張れー

古典流体と量子流体の根本的な違い
1. 古典流体が流体であるためには
2. 量子流体が流体であるためには
量子流体・古典流体が従う方程式
1. 古典流体が従う方程式
2. 量子流体
古典流体と量子流体が従う方程式はなぜ似ている？
1. 物理量を定義するための仮定は同じであったか？
2. 物理量が従う方程式の導出方法は似ていたか？
まとめ

古典流体と量子流体の根本的な違い

流体現象と言っても古典流体と量子流体はその流体であるための物理的理由が根本的に違います。まずは、それを理解しておきましょう(^^)/

古典流体が流体であるためには

流体力学をいわゆる連続体近似として扱う場合は、下記の記事に詳しく書きました。

あわせて読みたい

連続体かどうかの判断：クヌッセン数（クヌーセン数）

ここでは、かいつまんで古典流体が局所的な位置での密度\(\rho\)や速度\(\boldsymbol{v}\)と記述できる場合はどういった仮定があるのかを述べたいと思います。

下記の絵のように、古典流体（通常の流体）は、とてもミクロな領域を考えた時に、その領域内で粒子が多く存在しているために、粒子間相互作用が頻繁に起こると考えられます。

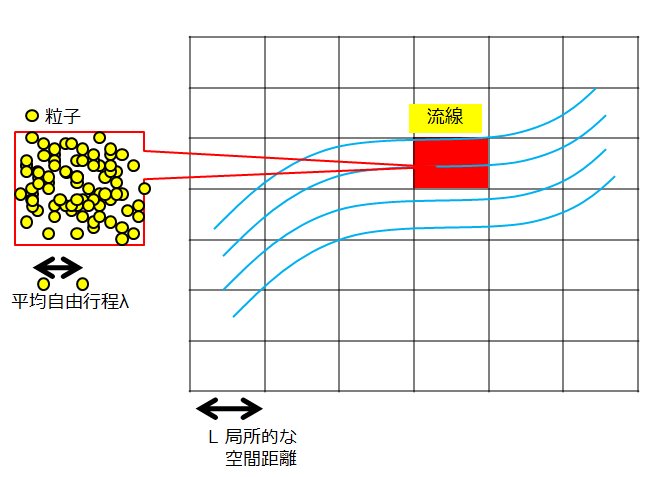
すると、そのミクロな領域内では物理量に分布など存在しせず（存在しても寄与が小さすぎる）、局所的には平均化したマクロな物理量を定義することができます。

量子流体が流体であるためには

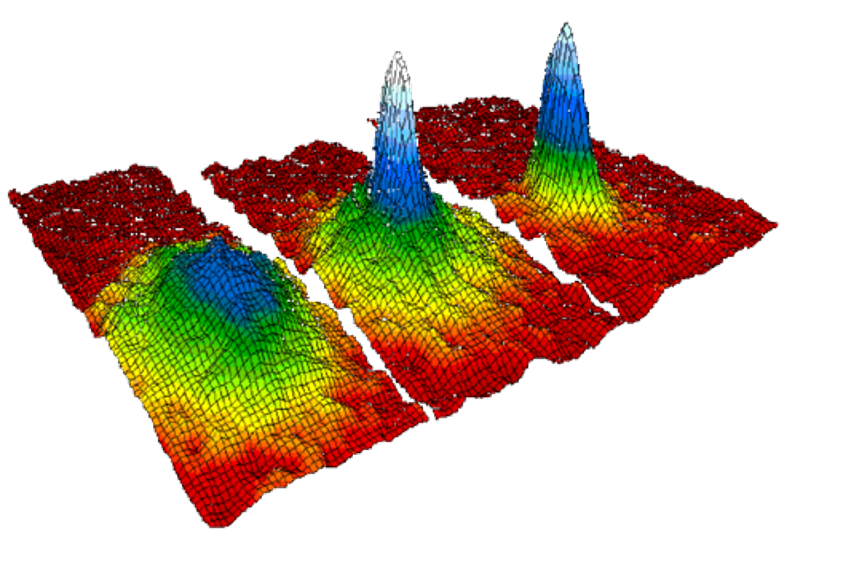
一方で、量子流体が流体現象を示す理由は古典流体とは異なります。

言い換えると、局所的な密度と速度を定義できる物理的理由が異なるということになります。では、量子流体で密度や速度を記述できる理由はなんだったでしょうか？

あわせて読みたい

低温状態で出現するボース・アインシュタイン凝縮体量子流体の出現

古典流体は、ミクロな領域での粒子の運動は個々で全くバラバラであるけども、それでもミクロな領域を考えるなら平均化して密度や速度を定義できたのに対して、

量子流体は、低温状態（絶対零度近傍）でボース・アインシュタイ凝縮によってほぼすべての粒子が最低エネルギー準位に落ち込むため、全ての状態は同じであるとして、秩序変数\(\psi\)を定義します。

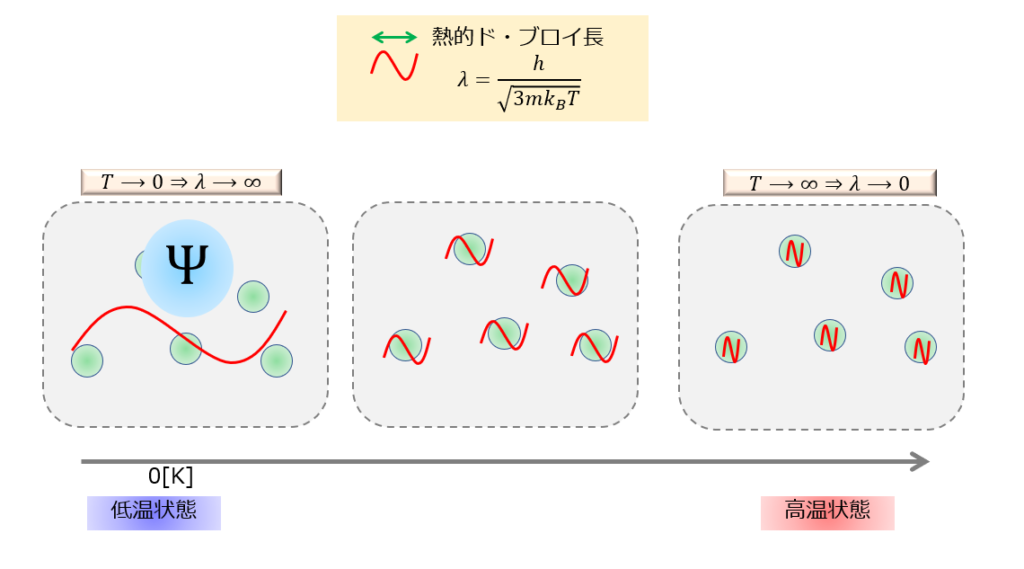
ゆえに、量子流体の場合は秩序変数（あるいは巨視的波動関数とも呼ぶ）\(\psi\)を、

\begin{align*}
\psi(\boldsymbol{r},t)=\sqrt{n}e^{i\theta}\tag{1}
\end{align*}

と書くことで、量子流体の流体は二つの変数（密度\(n\)と速度に起因する位相\(\theta\)）で特徴づけられることになります。

量子流体・古典流体が従う方程式

では、古典流体と量子流体がどのような方程式に従うのかを個別に見ていきましょう(^^)/

古典流体が従う方程式

古典流体で知りたい物理量とその物理量を知るための方程式はなんでしょうか？

まず、知りたい物理量は、

運動学的な物理量：流速\(\boldsymbol{v}\) 3成分
熱力学的な物理量：圧力\(p\)、密度\(\rho\)、温度\(T\)などから2つ

この5つになります。

あわせて読みたい

流体力学「5つの独立な物理量」と「5つの独立な基礎方程式」

ということは・・・・用意するべき方程式はの数は？？

5つですよね(^^)/

古典流体が従う方程式は以下の3種類（式の数は5つ）つです。

質量保存則

\begin{align*}\frac {\partial \rho }{\partial t}+\frac{\partial \rho v_{j}}{\partial x_{j}}=0\tag{2}\end{align*}

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\tag{3}\end{align*}

※\(x,y,z\)方向があるので、式の数は3つであることに注意。

エネルギーの保存則

\begin{align*}\frac{\partial \rho E}{\partial t}+\frac{\partial \rho E v_{j}}{\partial x_{j}}=-\frac{\partial q_{j}}{\partial x_{j}}+\frac{\partial \sigma_{ij}v_{i}}{\partial x_{j}}+\rho K_{j}v_{j}+Q\tag{4}\end{align*}

\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e：内部エネルギー

熱力学の状態方程式

\begin{align*}f(P,T,\rho)=0\tag{5}\end{align*}

熱力学の状態方程式もありますが、流体力学の基本的な変数は、

運動学的な物理量：流速\(\boldsymbol{v}\)
熱力学的な物理量：圧力\(p\)、密度\(\rho\)

です。

しかし、エネルギーの保存則が温度\(T\)を使って記述しているため、変数がひとつ増えてしまっていることになっています。

そこで、熱力学の状態方程式を使って、温度\(T\)を圧力\(p\)や密度\(\rho\)と結びつけるための方程式を用意する必要があるのです。

気体の場合は、多くの場合は理想気体の方程式(\(pV=nRT\))かもしれませんが、必ずしもそうとは限らないということは注意しておきましょう。

もし、仮に密度変化を考慮しなくても良いような非圧縮性の仮定を入れるのであれば、解くべき方程式は「質量保存則」と「運動量保存則」のみです。

なぜなら、密度\(\rho\)が変数ではなくなり、変数は速度\(\boldsymbol{v}\)と圧力\(p\)の4つだけなので、解くべき方程式は「質量保存則」と「運動量保存則」だけで良いということになります。

※速度は3成分あり、それに応じて運動量保存則も3成分あることに注意しましょう。

非圧縮性についての記事は以下に書いてあります。

あわせて読みたい

流体力学の非圧縮性と圧縮性
 非圧縮性流体の基礎方程式

量子流体

では、量子流体において知りたい物理量とその物理量が従う方程式は何だったでしょうか？

まず、量子流体で知りたい物理量は、

秩序変数\(\psi(\boldsymbol{r},t)\)

のみです。

カマキリ

え？これだけ？

これだけです。
ここが、古典流体との大きな違いでしょう。

そして、その秩序変数\(\psi(\boldsymbol{r},t)\)を求めるための方程式は、

グロス・ピタエフスキー方程式（略してGP方程式）

\begin{align*}
i\hbar\frac{\partial \psi(\boldsymbol{r})}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi(\boldsymbol{r})+V_{ex}\psi+g|\psi(\boldsymbol{r})|^2\psi(\boldsymbol{r})\tag{6}
\end{align*}

だけです。

カマキリ

古典流体よりもシンプルだな・・・

古典流体よりもとてもシンプルですよね。

しかし、これだけでは、物理的な意味を考えにくいので、秩序変数\(\psi(\boldsymbol{r},t)\)を

\begin{align*}
\psi(\boldsymbol{r},t)=\sqrt{n}e^{i\theta}\tag{7}
\end{align*}

と、粒子数\(n(\boldsymbol{r},t)\)と、速度に関係した位相\(\theta(\boldsymbol{r},t)\)に分解します。

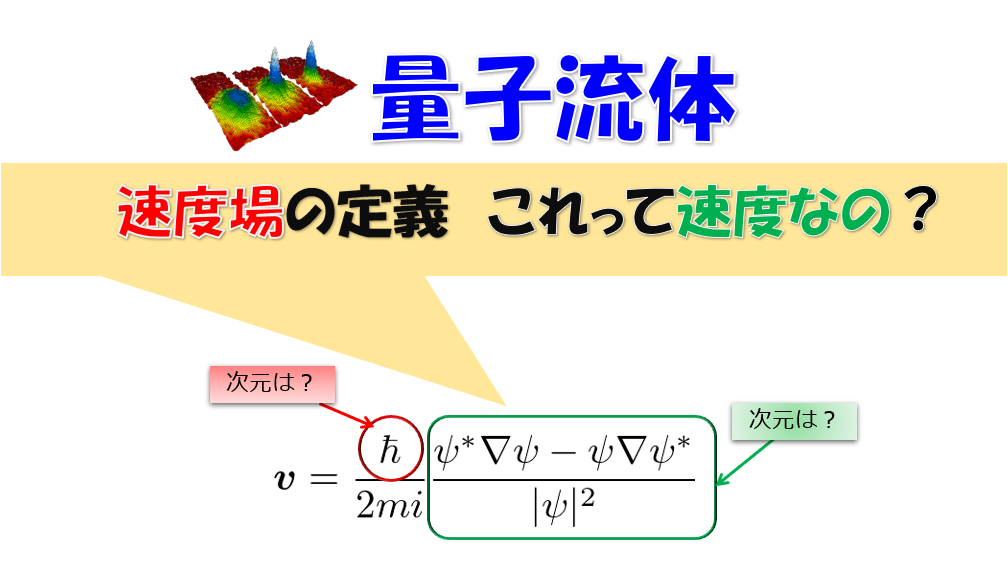
速度場

\begin{align*}
\boldsymbol{v}=\frac{\hbar}{m}\nabla\theta\tag{8}
\end{align*}

と、速度場を定義することにより、以下のような連続の式と運動量保存則を導出できます。

連続の式

\begin{align*}
\frac{\partial n}{\partial t}+\nabla\cdot\big(n\boldsymbol{v})=0\tag{9}
\end{align*}

運動量保存則（オイラー方程式：量子流体バージョン）

\begin{align*}
\frac{\partial \boldsymbol{v}}{\partial t}=-\frac{1}{mn}\nabla p-\nabla\bigg(\frac{\boldsymbol{v}^2}{2}\bigg)-\frac{1}{m}\nabla V+\frac{1}{m}\nabla\bigg(\frac{\hbar^2}{2m\sqrt{n}}\nabla^2\sqrt{n}\bigg)\tag{10}
\end{align*}

量子流体の場合は、絶対零度近傍での現象を対象にしているのでここでは温度は変数として考える必要がありません。

ですので、温度場を解くための方程式は用意されていません。（用意する必要がありません）

※超流動ヘリウムや希薄原子気体BECを総称して量子流体と呼んでいますが、「超流動ヘリウムも(6)式に従うのですか？」という誤解を生じるかもしれません。

定性的に超流動ヘリウムも(6)式の理解で良いかもしれませんが、厳密には(6)式には従いません。

あわせて読みたい

低温状態で出現するボース・アインシュタイン凝縮体量子流体の出現

↑こちらの後半に記載しております。

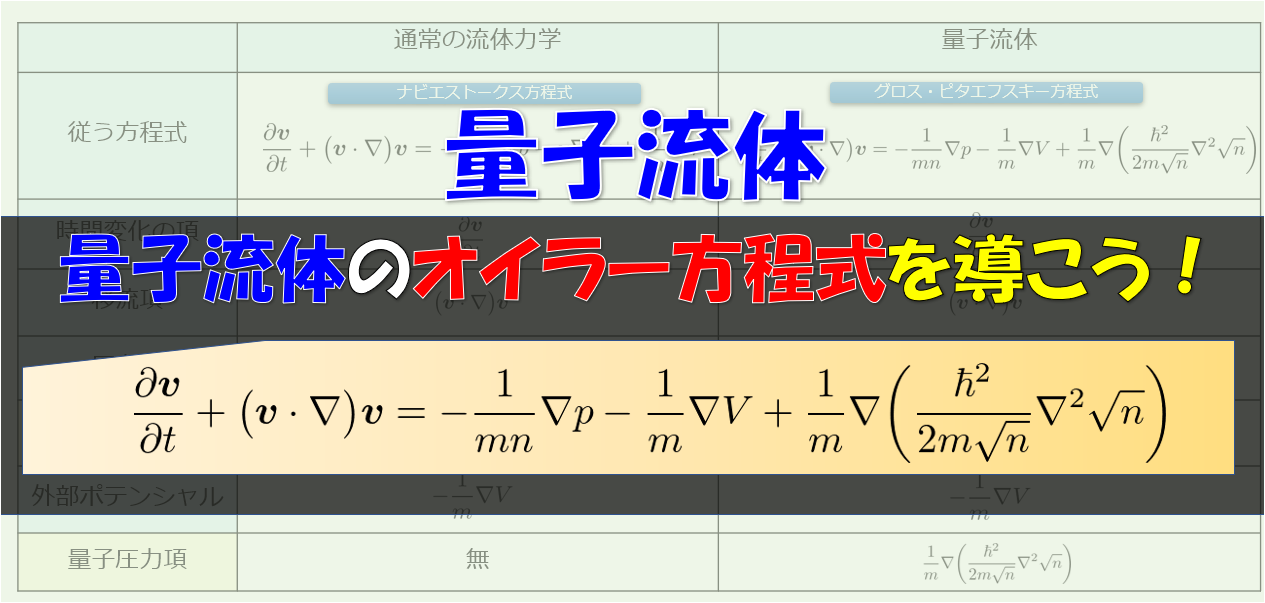
古典流体と量子流体が従う方程式はなぜ似ている？

よくよく眺めてみると、古典流体と量子流体が従う方程式は結構似ていませんかね？

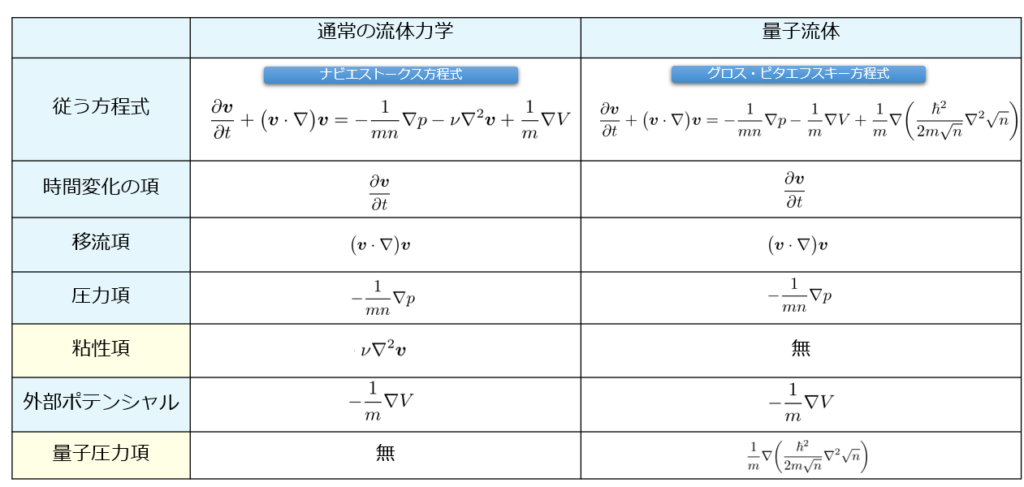
並べてみるとこんな感じです(^^)/

結構似ていますね。

なぜで似ているのでしょうか？？

これを理解するためには、以下の2つのことを思い出してみましょう。

物理量を定義するための仮定は同じであったか？
物理量が従う方程式の導出方法は似ていたか？

基本的にはこの2点を見ていけばよいのですよね。

物理量を定義するための仮定は同じであったか？

これは本記事の序盤に説明したように、古典流体と量子流体ではその物理量を定義するための物理的背景というのが違いましたよね。

古典流体は、あるミクロな領域を流体粒子として平均化して流速\(\boldsymbol{v}\)、密度\(\rho\)でまとめる。
量子流体は、全ての粒子が最低エネルギー準位に落ち込むこと秩序変数\(\psi\)でまとめる。

※局所速度\(\boldsymbol{v}\)、局所密度\(\rho\)を定義するときの物理的背景が違うということです。

物理量が従う方程式の導出方法は似ていたか？

確かに、古典流体と量子流体では物理量を定義するときの背景が違いましたけども、

なぜ、物理量が従う方程式は似ているのでしょうか？

それは、物理量の保存則の導出の仕方が似ているからですよね。

検査体積\(V\)を用意して、「単位時間あたりに減少した物理量\(\Phi\)は、何によって変化を受けたのか」というの考え方を古典流体でも量子流体でも行っているのです。

※任意の物理量（例）：速度\(\boldsymbol{v}\)、密度\(\rho\)

(A)単位時間当たりの物理量\(\Phi\)の減少量
=
(B)流れによる表面からの出入り
＋
(C)表面からの作用
＋
(D)検査体積内での発生・消滅、体積力による仕事

と、このように考えれば良いということになります。

あわせて読みたい

流体力学の基礎方程式の導出：一般形式

結論

古典流体と量子流体は、その物理量（局所速度\(\boldsymbol{v}\)、局所密度\(\rho\)）を定義するための物理的背景は異なるけども、それらの物理量が保存するという「保存則の上で導出された式」であるために古典流体と量子流体が従う方程式はよく似ている。

ということになります。

まとめ

本記事のテーマは以下の内容でやっていきましたが、少しでも内容を理解いただけましたでしょうか(^^)/

本記事の内容

「量子流体」と「古典流体」の物理的な本質の違いを知ろう
「量子流体」と「古典流体」の類似性を見よう

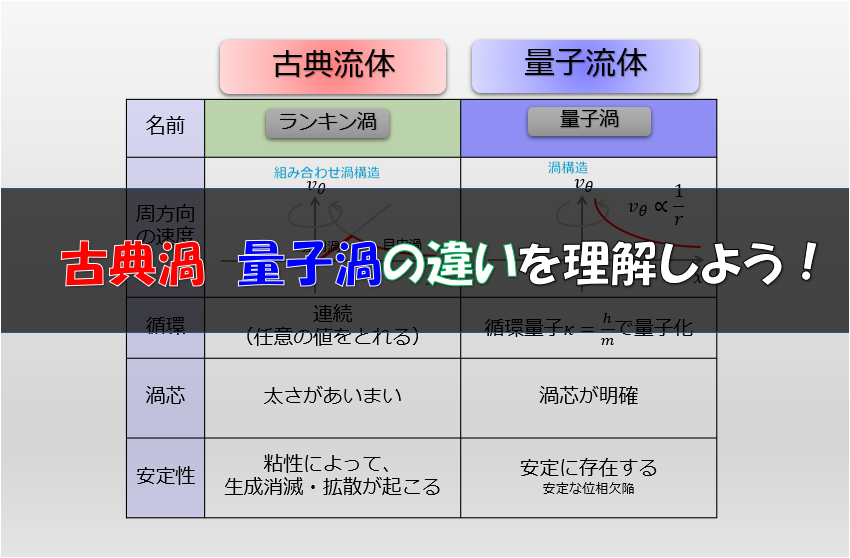
古典流体と量子流体は、どちらも流体現象であることには変わりありませんが、両者を定義づけるための物理的背景が全く異なるが従う方程式はよく似ているという面白い話をしました。

古典流体と量子流体の方程式はよく似ているのに、”物理的性質は全く異なる”という面が多くあります。（もちろん類似する点も多くあります）

詳しい類似性・相違点は別途記事でまとめたいと思います!(^^)!

というわけで古典流体と量子流体の違いを知るための超入門編の内容でした。

量子流体力学と古典流体力学の「似ている点・異なる点」を解説しよう！