流体力学の基礎式であるエネルギー保存則についての記事を書きたいと思います(^^)/
流体力学のエネルギー保存則の導出の仕方を知りたい方
タイトル通り、流体力学におけるエネルギー保存則を簡単に導出したいと思うのですが、ほとんどの書籍は、
- 質量保存則
- 運動量保存則
- エネルギー保存則
を別個で導きますよね。
でも、実は保存則のという同じ考え方を用いて、どれも次に示す基礎方程式の一般系から導くことができますのですよね。
基礎方程式の一般系
これは、単位時間あたりに変化した物理量(左辺)が、何によって変化したか(右辺)を記述すれば導けます。
流体の基礎方程式は下記の(1)~(3)なのですが、ひとつひとつ別個に覚えるのではなくて、全て上記の一般系(\(\diamondsuit\))の形から導出されるということを覚えておいた方がよいでしょう。
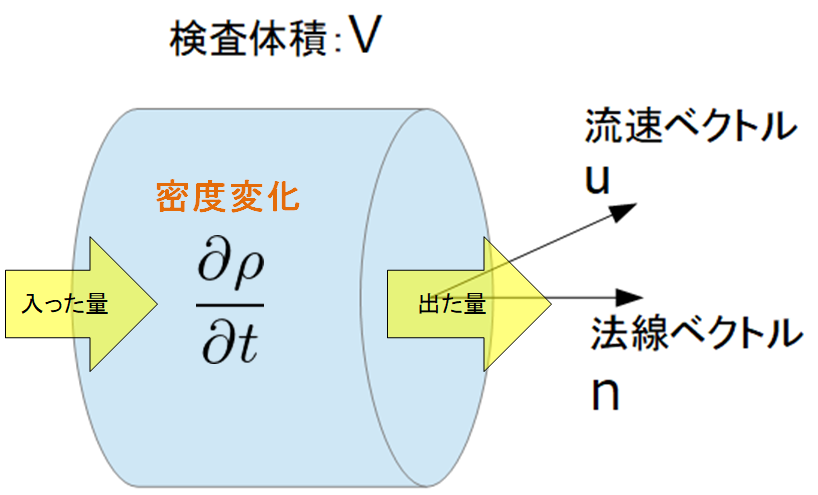
質量保存則
運動量保存則
エネルギーの保存則
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
熱力学の状態方程式
そこで、本記事は、
エネルギー保存則
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
を導出したいと思います。
本記事は下記の参考文献のお力を借りました。
理学部向けで、ここまで丁寧に流体力学の理論を書いてある本もなかなか珍しいです。
※前編のみしか出版されていないのが痛いですが、持っていて損しない参考書でしょう。
エネルギー保存則の各項が何かを確認する
まずはエネルギー保存則の各項を確認しておきましょう。
※(3)式のままでは考えにくいため、左辺第一項を右辺に移項します。
とても複雑な式に感じますが、各項は何かをおさえておきましょう。
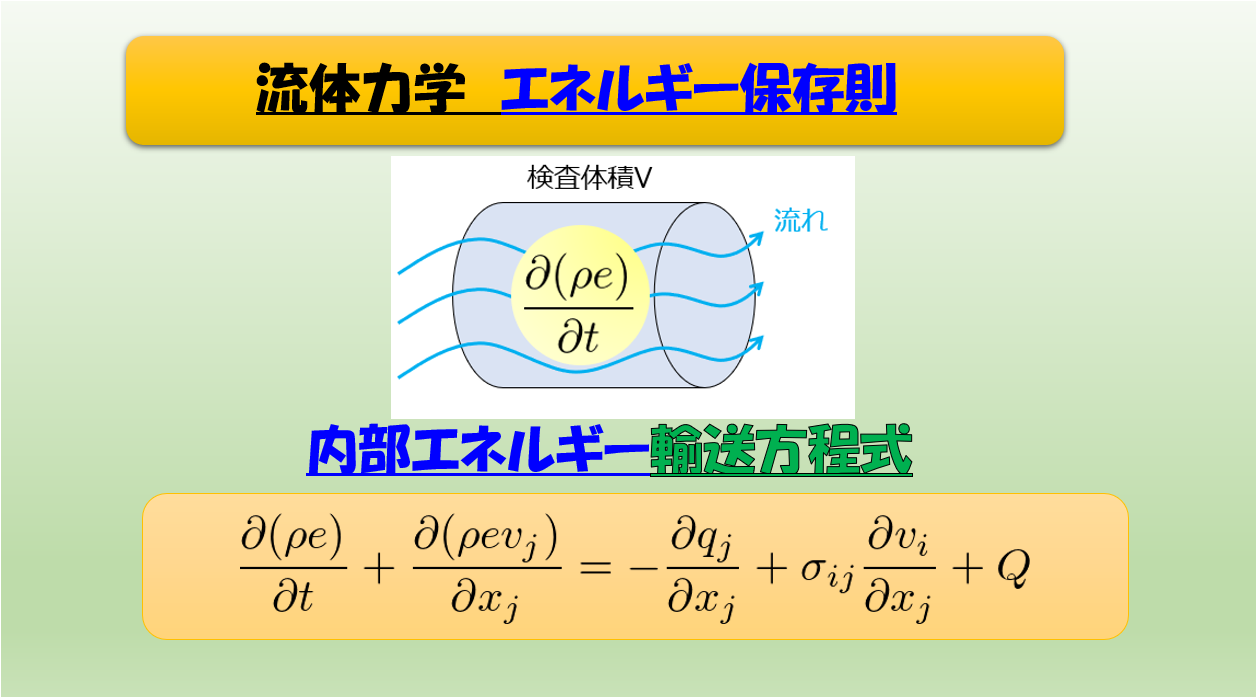
下記のように検査体積を用意します。
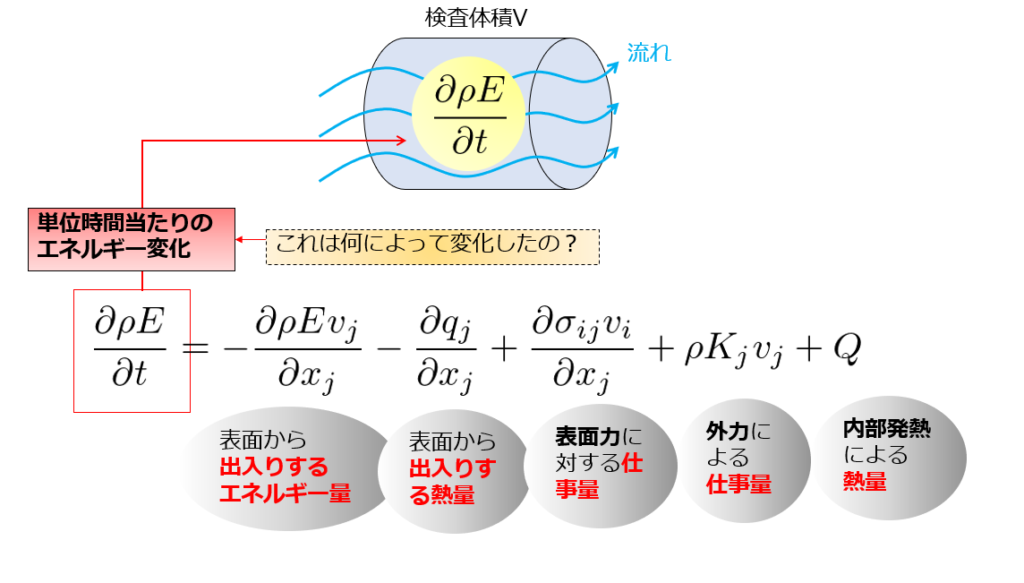
ステップは次の通り
この検査体積と呼ばれる領域で、
- 「単位時間あたりにどれだけエネルギー変化しましたか?」をまず考え、左辺に置く。
- 「その変化をもたらした原因は何か?」を右辺に書き並べれる。
このようにして流体力学のエネルギー保存則を導くことができます。
基礎方程式の一般系も同じ考え方
冒頭に書きました、基礎方程式の一般系(\(\diamondsuit\))も同じ考え方で導出しておいたのですよね。
基礎方程式の一般系
これは、単位時間あたりに変化した物理量(左辺)が、何によって変化したか(右辺)を記述すれば導けます。

を考えれば基礎方程式の一般系が導けたのですから、物理量\(\Phi\)を、運動量\(\rho E\)とすると、(\(\diamondsuit\))式は「エネルギー保存則」になります。
というわけで(A)(B)(C)(D)という順番で考えていけば、エネルギー保存則を導くことができるのです。
ここでの流体によるエネルギー量\(E\)は2つ考えられます。
- 流速による運動エネルギー\(\frac{1}{2}\rho \boldsymbol{v}^2\)
- 流体内部にもつ内部エネルギー\(e\)
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
内部エネルギーとは何かという補足を書いておきます
内部エネルギーとは熱力学でも登場する実態はよくわからない(僕がわかっていないだけかも)エネルギーです。
熱力学第一法則から\(dQ=dU+dW\)と書くと\(U\)が内部エネルギーを意味しています。
熱力学の第一法則は、エネルギーの保存則(吸収した熱量=内部に蓄えられるエネルギー+外部にする仕事)という考え方をしますが、あれ?って思いますよね。
どうして右辺はこれだけなの?
- 流体の運動エネルギーは?
- 位置エネルギーは?
これらはどこにいったでしょうか?(‘ω’)
本当は\(U\)はこうなのではないでしょうか・・・
$$U=U_{p}+U_{g}+U_{in}$$
※\(U_{p}\):運動エネルギー
※\(U_{g}\):位置エネルギー
※\(U_{in}\):内部エネルギー
しかし、よく考えれば熱力学の第一法則は各項は変化量です。
しかも、熱力学はマクロな物理量として密度や圧力や温度を与えているので、流体現象のようものは考えていません。
検査体積みたいなものを考えると、左からされた仕事量・運動エネルギーは右側にも同じだけなされるのですから、変化量は無視できるくらいであると考えても良いでしょう。
つまり流れがあろうとなかろうと、ミクロな視点で見ると個々の粒子は激しく運動しているので、それが内部エネルギーと解釈しても良いでしょう。
これはマクロな視点での物理量として温度と対応付けられるものです。
イメージするなら気体分子運動論なんてのはちょうどよいでしょう。
※気体分子運動論は「理想気体」に対して考えられている現象なので、そこだけ注意を(‘ω’)
では、本題に戻ります。
(A)単位時間当たりの運動量\(\rho E\)の減少量
任意の検査体積\(V\)内で、単位時間当たりのエネルギーの減少量は、(\(\diamondsuit\))の左辺をエネルギー量:\(\Phi=\rho E\)と置くことで求めることができます。
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
(B)流れによる表面からの出入り
続いて、任意の検査体積の表面から出入りするエネルギー量を計算しましょう。
それは、(\(\diamondsuit\))の右辺の第一項を運動量:\(\Phi=\rho E\)とすることで求めることができます。
(C)表面からの作用
続いて、検査体積にはたらく作用(表面からの作用)を考えるのですが、どのような作用があるでしょうか。
- 出入りする熱量の総和\(\boldsymbol{q}\)
- 表面力がなる仕事(応力ベクトル\(\boldsymbol{t}\))
出入りする熱量の総和\(\boldsymbol{q}\)
最後の部分は、ガウスの発散定理を使っています。
表面力がなる仕事(応力ベクトル\(\boldsymbol{t}\))

最後の部分は、ガウスの発散定理を使っています。
検査体積内での発生・消滅、体積力による仕事
検査体積内での発生・消滅、体積力による仕事は以下の2つがあります。
- 外力による仕事量
- 内部発熱
外力による仕事量
(\(\diamondsuit\))一般式の第三項について、単位質量あたりの\(i\)方向の力(\(K_{i}\))を用いると、外力は\(rho K_{i}\))となります。
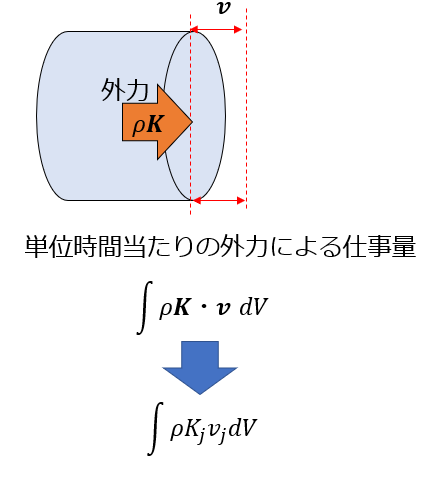
では、単位時間当たりの仕事量は、
となります。
内部発熱
単位時間当たりの内部発熱は、\(b=Q\)とおくと、
となります。
(A)(B)(C)(D)をまとめると・・・
↑これに従って、(5)(6)(7)(8)(9)(10)を書くと、
\(\int \frac{\partial(\rho E)}{\partial t} dV\)
\(=-\int \frac{\partial \big(\rho Ev_{j}\big)}{\partial x_{j}}dV\)
\(-\int \frac{\partial q_{j}}{\partial x_{j}}dV\)
\(+\int \frac{\partial \sigma_{ij}v_{i}}{\partial x_{j}}dV\)
\(+\int \rho K_{j}v_{j}dV\)
\(+\int Q dV\cdot\cdot\cdot (11)\)
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
ここで、検査体積\(V\)は任意に選べるわけですので、どんな検査体積に対しても(11)式が成り立つはずです。
\(\frac{\partial(\rho E)}{\partial t} \)
\(=-\frac{\partial \big(\rho E v_{j}\big)}{\partial x_{j}}\)
\(- \frac{\partial q_{j}}{\partial x_{j}}\)
\(+ \frac{\partial \sigma_{ij}v_{i}}{\partial x_{j}}\)
\(+\rho K_{j}v_{j}\)
\(+ Q \cdot\cdot\cdot (12)\)
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
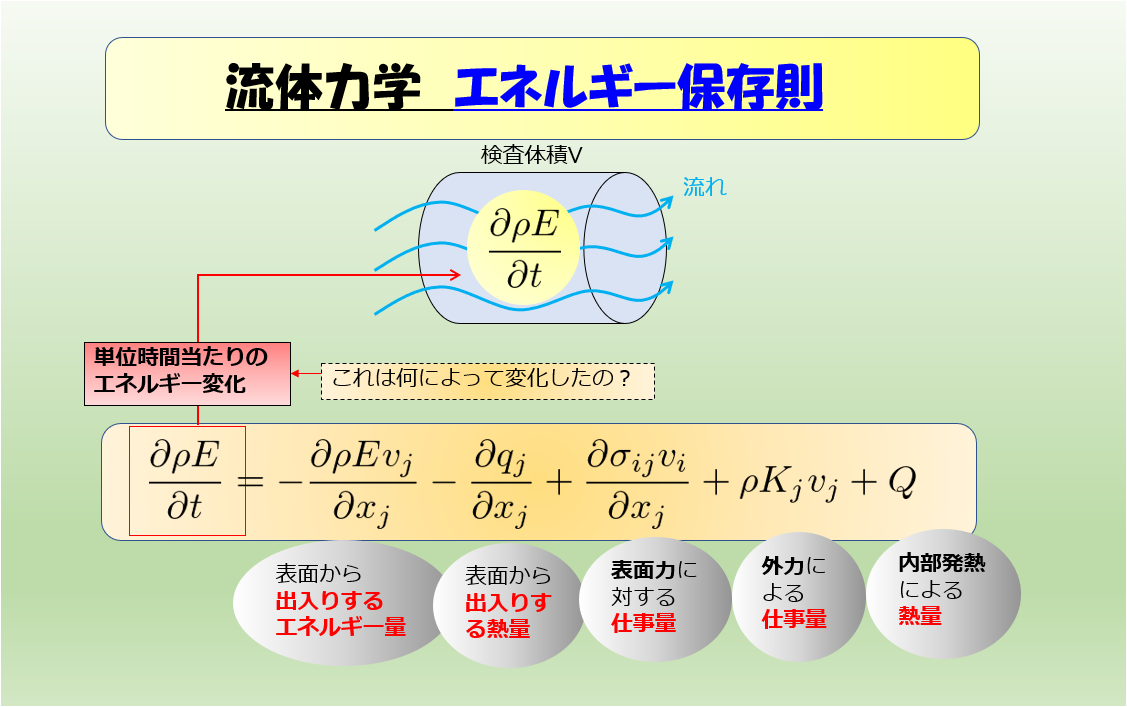
これが流体力学のエネルギー保存則です。
エネルギー保存則
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
まとめ
目標としているエネルギー保存則を導くことができました。
基礎方程式の一般系
において、「運動量:\(\Phi=\rho E\)」、「表面力による仕事量\(a=t_{i}u_{i}=\sigma_{ij}n_{i}u_{i}\)」、「外力による仕事量:\(b=\rho K_{j}v_{j}\)、内部発熱:\(b=Q\)」として、代入すると、↓エネルギー保存則が導けました。
エネルギー保存則
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
実はここは中間のまとめなのです。
ここからさらに内部エネルギーの輸送方程式を導くことができます。





















Φ=ρEとのことですが…左辺第1項目のΦv_jのv_jは一体どこに消えたのでしょうか…?
(5)式以降から抜けていただけでしたね…失礼いたしました。
お読み頂きありがとうございます。
大変失礼しました。
修正しました。
ご指摘頂きありがとうございます。