どうも(@t_kun_kamakiri)(‘◇’)ゞ
前回は、流体力学のエネルギー保存則を導きました。
↓こちらです。
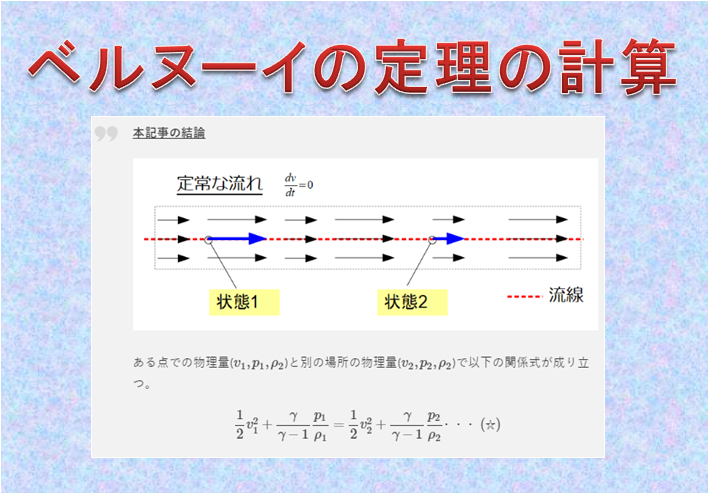
↑上の記事でどういった結論が出たのかをおさらいしましょう。
基礎方程式の一般系
において、
「運動量:\(\Phi=\rho E\)」、「表面力による仕事量\(a=t_{i}u_{i}=\sigma_{ij}n_{i}u_{i}\)」、「外力による仕事量:\(b=\rho K_{j}v_{j}\)、内部発熱:\(b=Q\)」として、代入すると、
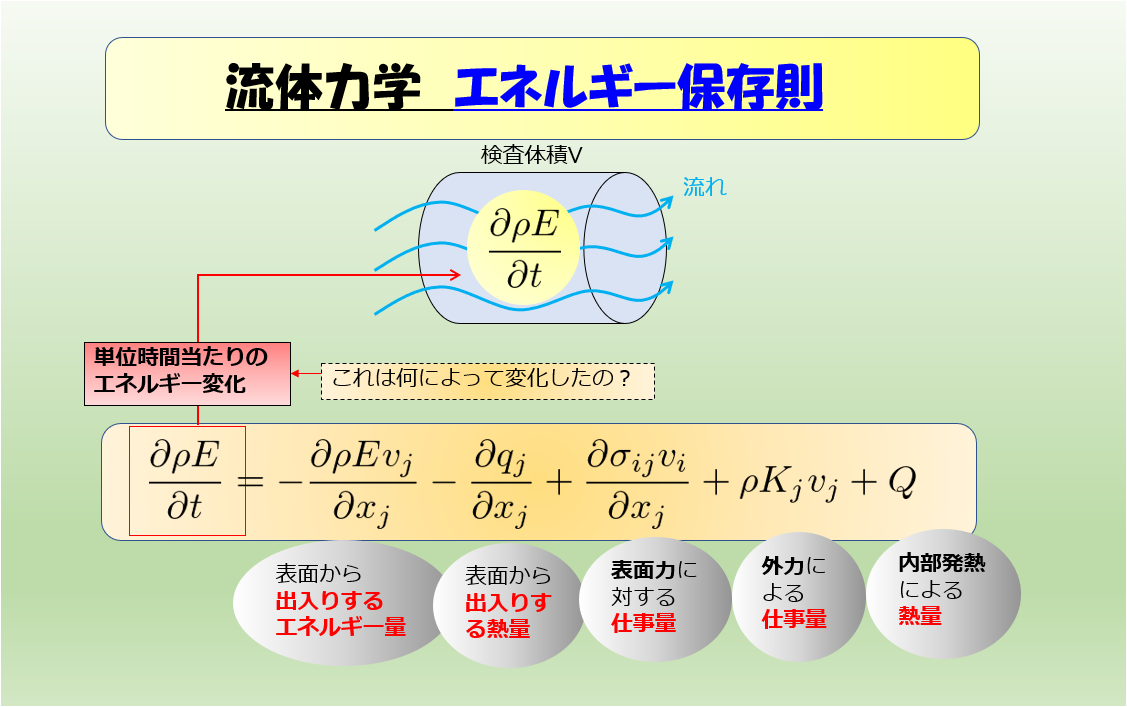
↓エネルギー保存則が導けました。
エネルギー保存則
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e:内部エネルギー
実はここまでは、エネルギー保存則についての途中経過だったのです。
本記事で解説する内容
このエネルギー保存則を式変形していって・・・
に流速による運動エネルギー\(\frac{1}{2}\boldsymbol{v}^2\)が入っていますが、邪魔なので消去することを考えます。
そうすると以下の式が導かれます。
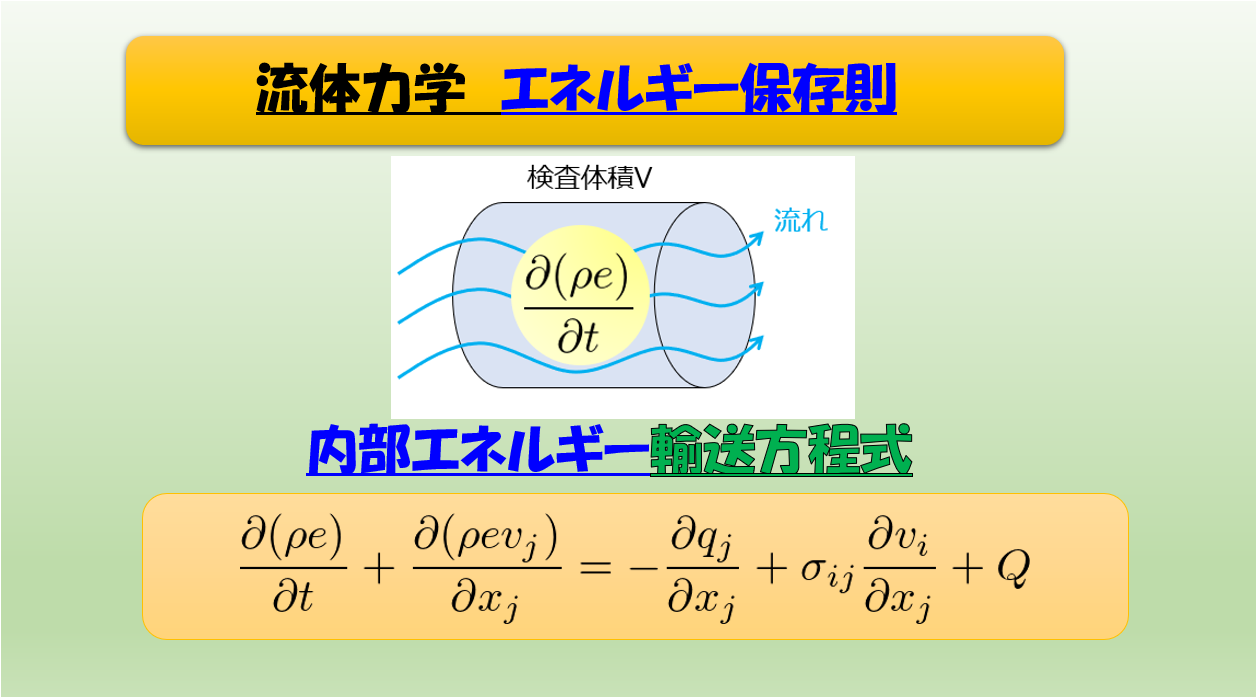
(1)内部エネルギーの輸送方程式
\frac{\partial (\rho e)}{\partial t}+\frac{\partial (\rho ev_{j})}{\partial x_{j}}= -\frac{\partial q_{j}}{\partial x_{j}}+\sigma_{ij}\frac{\partial v_{i}}{\partial x_{j}}+Q\tag{2}
\end{align*}
内部エネルギーの輸送方程式を導きましょう(^^)/
そうすると、検査体積内での内部エネルギー\(\rho e\)の変化を表す式に変えることができます。
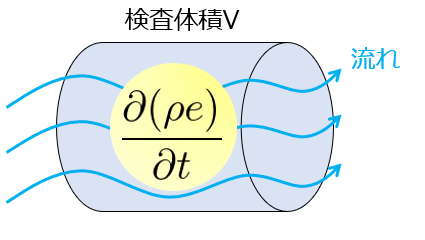
※(1)(2)式は一見別の式を導いたように見えますが、実は全く同じエネルギーの保存則に過ぎません。
流体力学の運動量保存則で速度についての情報を持った方程式があるのに、エネルギー保存則でも速度についての情報を持った(1)式である必要がないために、(2)式のように内部エネルギーだけの情報を持ったエネルギー輸送方程式に変えているだけです。
内部エネルギーの変化に式変形する
内部エネルギー\(\rho e\)の変化を表す式を式変形して導きます。
質量保存則と運動量保存則を用いて(3)式から流速による運動エネルギー\(\frac{1}{2}\rho\boldsymbol{v}^2\)を消去。
↓こちらを使います。
- 質量保存則
- 運動量保存則
では、(13)式に\(E=e+\frac{1}{2}\boldsymbol{v}^2\)を代入します。
\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
\(\boldsymbol{v}^2=v_{i}v_{i}\)と表記を変えました。
e:内部エネルギー
エネルギー保存則の微分をバラバラにする
エネルギー保存則を式変形していきます。
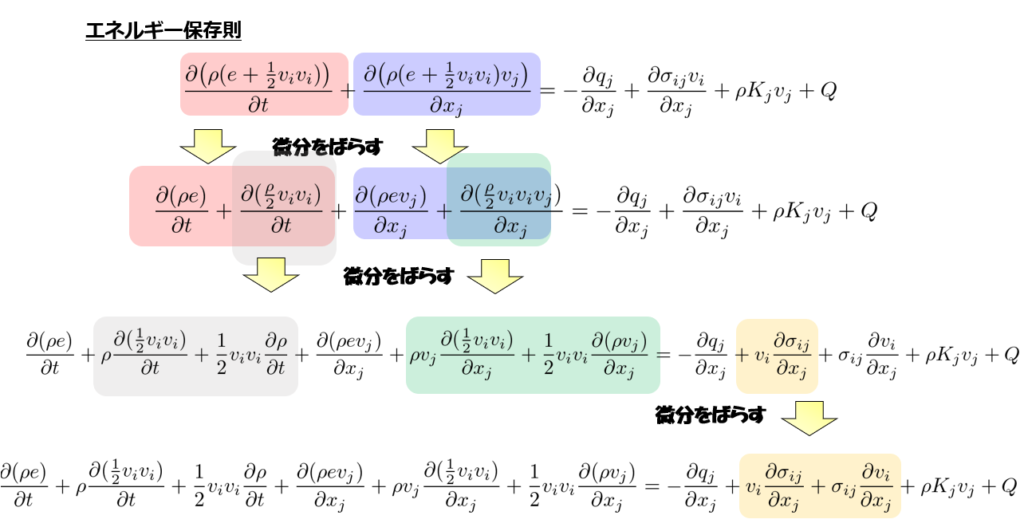

添え字に注意しながら、腕力でゴリゴリやります。
運動量保存則の微分をバラバラにする
同様に運動量保存則も式変形します。
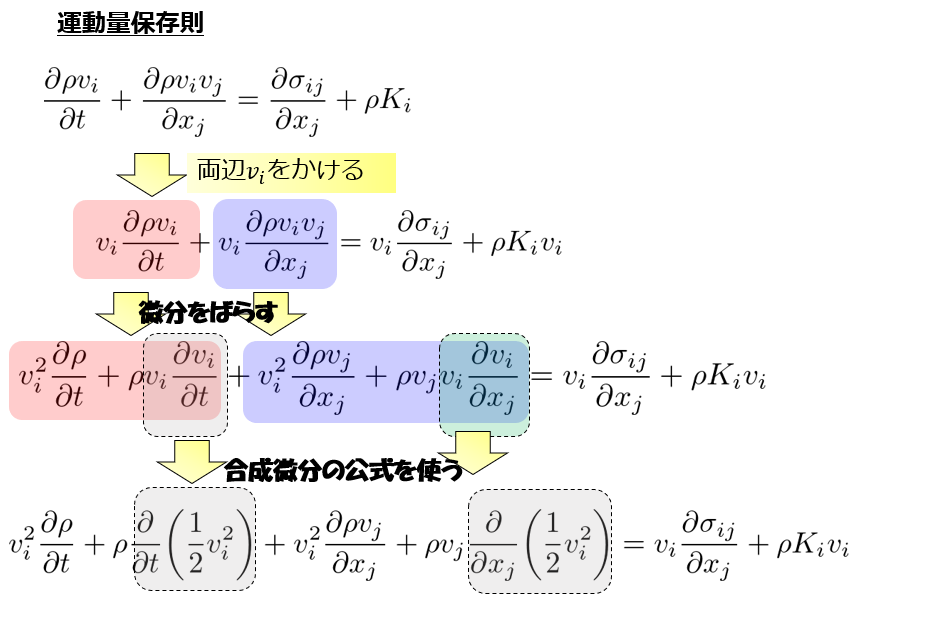

これも添え字に注意しながら、腕力でゴリゴリやります。
引き算する
先ほど計算した「エネルギー保存則」から「運動量保存則」を引きます。
このときに質量保存則を使うと消える項がいくつか見受けられるので、消しておきます。
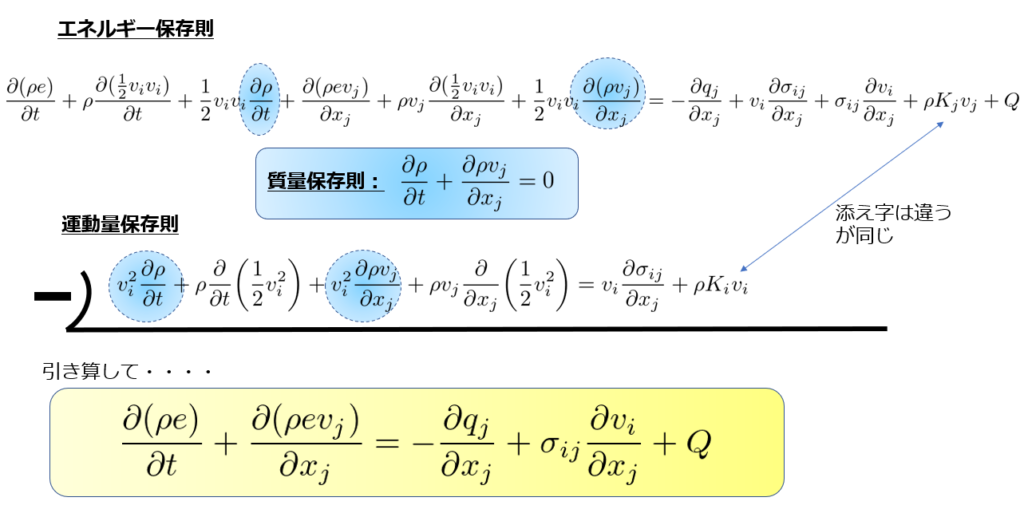

最終的に内部エネルギーの輸送方程式ができました(^^)/
まとめ



内部エネルギーの輸送方程式
内部エネルギーといわれてもあまりピンと来ないかもしれませんが、
熱力学の知恵も借りながらもう少し式変形することで、エンタルピーの輸送方程式や温度場の輸送方程式を導くことができます。
ひとまず今回導いた内部エネルギーの輸送方程式は、内部に蓄えられているエネルギーが流れに乗って運ばれているというイメージを持っておくことにしますm(_ _)m
参考文献
流体力学の理論と数値計算での理解を深めるのに良い参考文献を3つ紹介しておきます。
特に非圧縮性の流体の解説が多いですが、粘性流体に対する基礎方程式についての導出はかなり丁寧に解説されています。
こちらは流体の数値計算の解説が丁寧にまとめられた参考書です。 前半に流体の基礎方程式を導く解説が丁寧にまとめまとめられており、初学者にとって「理論面」と「数値計算」の両方を学ぶことができる良書だと思います。
こちらはPythonコードを使った数値流体の実装を題材にした参考書です。
Pythonは初学者にも易しい言語だと思いますのでプログラミングを学びたい方にはお勧めの参考書です。