流体力学の運動量保存則の導出｜宇宙に入ったカマキリ

流体力学の基礎式である運動量保存則についての記事を書きたいと思います(^^)/

どんな人に読んでほしいか

流体力学の運動量保存則の導出の仕方を知りたい方

タイトル通り、流体力学における運動量保存則を簡単に導出したいと思うのですが、ほとんどの書籍は、

質量保存則
運動量保存則
エネルギー保存則

を別個で導きますよね。

でも、実は保存則のという同じ考え方を用いて、どれも次に示す基礎方程式の一般系から導くことができますのですよね。

基礎方程式の一般系

\begin{align*}\int \frac{\partial \Phi}{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (\diamondsuit)\end{align*}

これは、単位時間あたりに変化した物理量（左辺）が、何によって変化したか（右辺）を記述すれば導けます。

あ基礎方程式の導出の記事はこちら

流体力学の基礎方程式の導出：一般形式

流体の基礎方程式は下記の(1)～(3)なのですが、ひとつひとつ別個に覚えるのではなくて、全て上記の一般系(\(\diamondsuit\))の形から導出されるということを覚えておいた方がよいでしょう。

質量保存則

\begin{align*}\frac {\partial \rho }{\partial t}+\frac{\partial \rho v_{j}}{\partial x_{j}}=0\cdot\cdot\cdot (1)\end{align*}

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

エネルギーの保存則

\begin{align*}\frac{\partial \rho E}{\partial t}+\frac{\partial \rho E v_{j}}{\partial x_{j}}=-\frac{\partial q_{j}}{\partial x_{j}}+\frac{\partial \sigma_{ij}v_{i}}{\partial x_{j}}+\rho K_{j}v_{j}+Q\cdot\cdot\cdot (3)\end{align*}

\(E=e+\frac{1}{2}\boldsymbol{v}^2\)
e：内部エネルギー

熱力学の状態方程式

\begin{align*}f(P,T,\rho)=0\cdot\cdot\cdot (4)\end{align*}

そこで、本記事は、

本記事の内容

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

を導出したいと思います。

右辺の第一項を理解するのに、コーシー応力を理解している必要があるので、初見の方は下記の記事を事前に読んでおくことをお勧めします。

事前に読んでほしい記事

考え方
（\(\diamondsuit\)）の一般系から「運動量保存則」の導出
(A)(B)(C)(D)をまとめてみます
まとめ
補足説明
1. 圧縮性の流体についても成り立つ式
2. ニュートン流体か非ニュートン流体かの区別はしていない

考え方

運動量保存則を導出する考え方はとてもシンプルで・・・

(A)単位時間当たりの物理量\(\Phi\)の減少量

(B)流れによる表面からの出入り

＋

(C)表面からの作用

＋

(D)検査体積内での発生・消滅、体積力による仕事

を考えれば基礎方程式の一般系が導けたのですから、物理量\(\Phi\)を、運動量\(\rho \boldsymbol{v}\)とすると、(\(\diamondsuit\))式は「運動量保存則」になります。

では、(A)(B)(C)(D)の順にひとつひとつ見ていきましょう。

（\(\diamondsuit\)）の一般系から「運動量保存則」の導出

下記の記事よりある物理量\(\Phi\)の輸送方程式を導出しました。

あわせて読みたい

流体力学の基礎方程式の導出：一般形式

結果は、↓これです。

\begin{align*}\int \frac{\partial \Phi}{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (\diamondsuit)\end{align*}

そのある物理量を決めれば、その物理量の輸送方程式が導出できるというわけですよね。

今回、そのある物理量とは「運動量：\(\Phi=\rho v_{i}\)」のことです。※\(i\)方向の運動量ってことです。

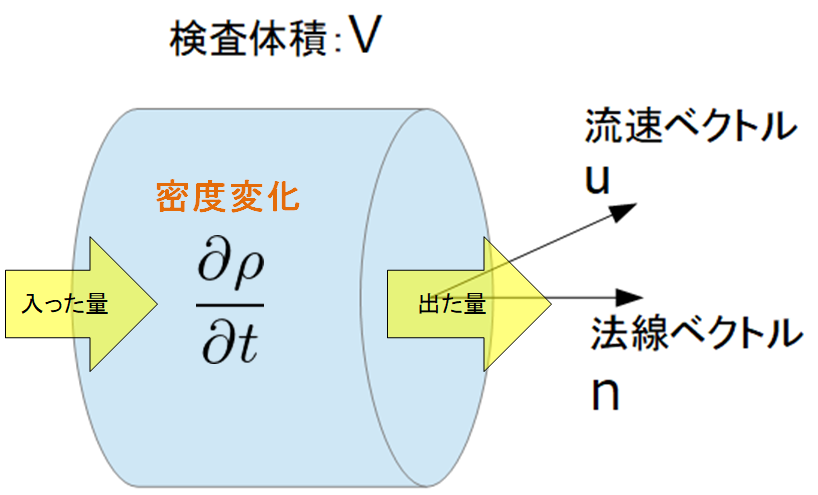
(A)単位時間当たりの運動量\(\rho v_{i}\)の減少量

任意の検査体積\(V\)内で、単位時間当たりの運動量の減少量は、（\(\diamondsuit\)）の左辺を運動量：\(\Phi=\rho v_{i}\)と置くことで求めることができます。

\begin{align*}\int \frac{\partial \Phi}{\partial t} dV=\int \frac{\partial (\rho v_{i})}{\partial t} dV\cdot\cdot\cdot (5)\end{align*}

(B)流れによる表面からの出入り

続いて、任意の検査体積の表面から出入りする運動量を計算しましょう。

それは、（\(\diamondsuit\)）の右辺の第一項を運動量：\(\Phi=\rho v_{i}\)とすることで求めることができます。

\begin{align*}-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV=-\int \frac{\partial \big(\rho v_{i} v_{j}\big)}{\partial x_{j}}dV\cdot\cdot\cdot (6)\end{align*}

(C)表面からの作用

続いて、検査体積にはたらく作用（表面からの作用）を考えるのですが、どのような作用があるでしょうか。

流体力学での作用といえば、次の2つです。

圧力
粘性抵抗（応力）

これらは、流体要素間にはたらく内力にあたります。

あわせて読みたい

流体力学コーシー応力の意味は圧力と粘性抵抗【図でわかりやすく解説】

で、そのときに流体要素間にはたらく「圧力」や「粘性抵抗（応力）」などの応力ベクトルをどのように記述したかというと、コーシー応力を用いて、

任意の面にはたらく応力ベクトル\(\boldsymbol{t}\)

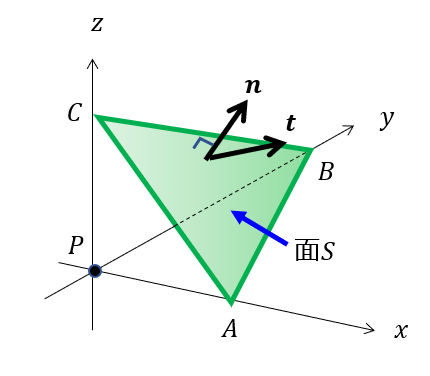
(1)式はこのように書いたりもします。

\begin{align*}t_{i}=\sigma_{ij}n_{i}\cdot\cdot\cdot (7)\end{align*}

※添え字が2回続くと和を意味しています（アインシュタインの縮約記法）。

と、このように書けたのですよね。

※\(\sigma_{ij}\)：コーシー応力

すんなり理解できない人には、こちらの記事をお読みください(^^)v

あわせて読みたい

検査体積にはたらく作用（表面からの作用）の表記には、この(7)式を用います。

(\(\diamondsuit\)）の第二項について、\(a=t_{i}\)とすると

\begin{align*}\int a dS=\int t_{i} dS=\int \sigma_{ij}n_{i} dS=\int \frac{\partial \sigma_{ij}}{\partial x_{j}}dV\cdot\cdot\cdot (8)\end{align*}

となります。

最後の部分は、ガウスの発散定理を使っています。

(D)検査体積内での発生・消滅、体積力による仕事

検査体積内での発生・消滅、体積力による仕事などのイメージはつきにくいですが、ここでは重力など常にかかっている外力などを考えると良いでしょう。

(8)式は内力についてでしたが、今度の作用は外力についてですね。

（\(\diamondsuit\)）一般式の第三項について、単位質量あたりの\(i\)方向の力(\(K_{i}\))を用いて\(b=\rho K_{i}\)とすると、

\begin{align*}\int b dV=\int \rho K_{i} dV\cdot\cdot\cdot (9)\end{align*}

となります。

(A)(B)(C)(D)をまとめてみます

再度、全体を見ます。

(A)単位時間当たりの物理量\(\Phi\)の減少量

(B)流れによる表面からの出入り

＋

(C)表面からの作用

＋

(D)検査体積内での発生・消滅、体積力による仕事

↑これに従って(5)(6)(8)(9)を書くと、

\(\int \frac{\partial (\rho v_{i})}{\partial t} dV\)

\(=-\int \frac{\partial \big(\rho v_{i} v_{j}\big)}{\partial x_{j}}dV\)

\(+\int \frac{\partial \sigma_{ij}}{\partial x_{j}}dV\)

\(+\int \rho K_{i} dV\cdot\cdot\cdot (10)\)

となります。

ここで、検査体積\(V\)は任意に選べるわけですので、どんな検査体積に対しても(10)式が成り立つはずです。

よって、

\(\frac{\partial (\rho v_{i})}{\partial t} \)

\(=-\frac{\partial \big(\rho v_{i} v_{j}\big)}{\partial x_{j}}\)

\(+ \frac{\partial \sigma_{ij}}{\partial x_{j}}\)

\(+ \rho K_{i}\cdot\cdot\cdot (11)\)

となります。

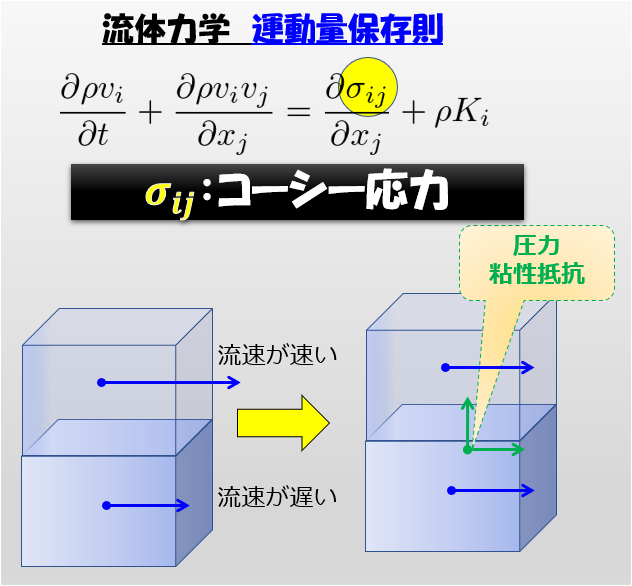
これが流体力学における運動量保存則の式なのです。

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

まとめ

基礎方程式の一般系

\begin{align*}\int \frac{\partial \Phi}{\partial t} dV=-\int \frac{\partial \big(\Phi v_{j}\big)}{\partial x_{j}}dV+\int a dS+\int b dV\cdot\cdot\cdot (\diamondsuit)\end{align*}

において、

「運動量：\(\Phi=\rho v_{i}\)」、「応力ベクトル\(a=t_{i}=\sigma_{ij}n_{i}\)」、「外力：\(b=\rho K_{i}\)」として、代入すると、

↓運動量保存則が導けました。

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

補足説明

運動量保存則

\begin{align*}\frac{\partial \rho v_{i}}{\partial t}+\frac{\partial\rho v_{i}v_{j}}{\partial x_{j}}=\frac{\partial \sigma_{ij}}{\partial x_{j}}+\rho K_{i}\cdot\cdot\cdot (2)\end{align*}

↑こちらは式には以下の点に注意しておきましょう。