流体力学

1次元のオイラーの運動方程式

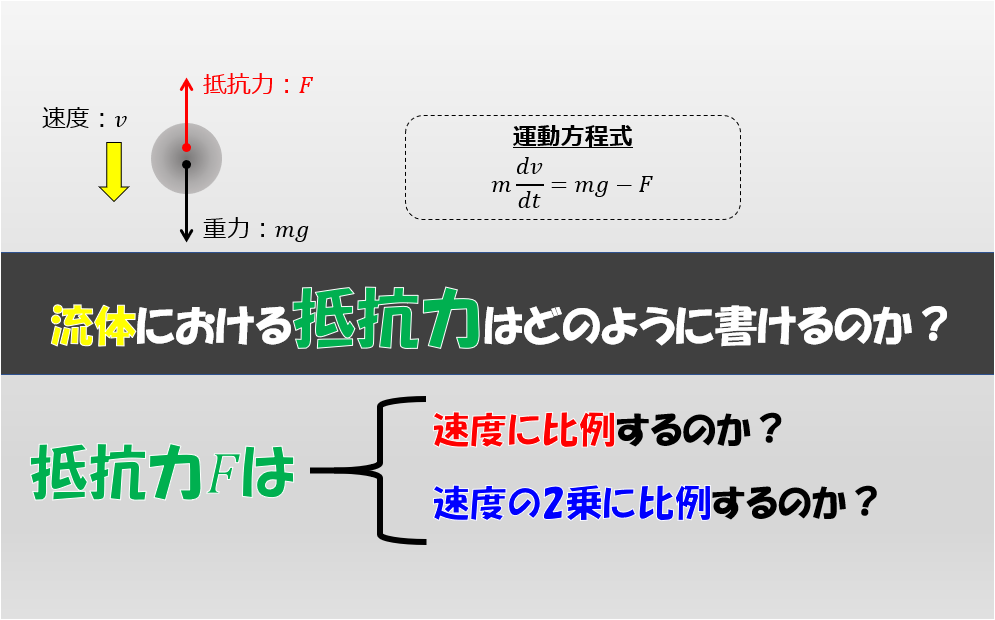
下記の記事で3次元の流体の基礎方程式をまとめたのですが、皆さんもご存知の通り、下記の式のナビエストークス方程式というのは解析的に（手計算で）解くことができません。

\begin{align*}\frac{\partial \boldsymbol{v}}{\partial t}+(\nabla\cdot\boldsymbol{v})\boldsymbol{v}=-\frac{1}{\rho}\nabla p+\nu\nabla^2 \boldsymbol{v}\cdot\cdot\cdot (1)\end{align*}

だからこそ流体力学における現象を理解する上では、ある程度の仮説を設けることが重要であり、そうすることでずいぶんと理解が進むことがあります。

あわせて読みたい

非圧縮性流体の基礎方程式

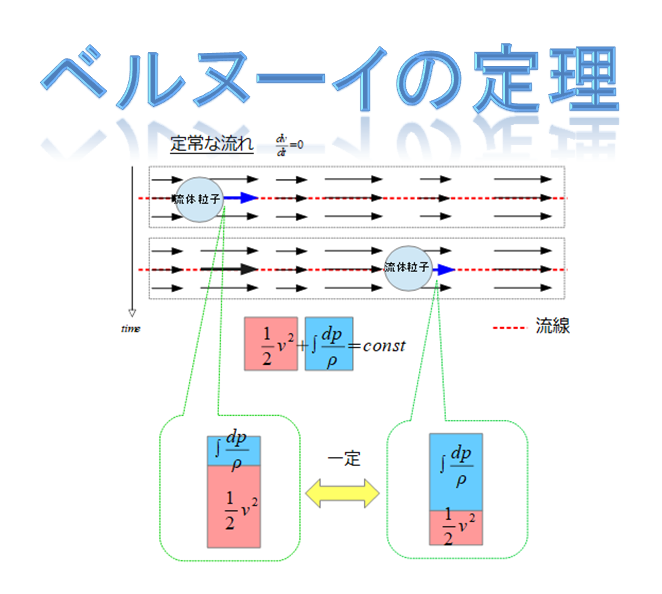
ここでは、ベルヌーイの定理といういわゆるエネルギー保存則について考えていきます。

そこでは、どういった仮定を入れていくかということは常に意識しておきましょう。

では、下記のような流れで「ベルヌーイの定理」まで導き、さらに流れの「臨界状態」まで説明したいと思います。

補足説明として、「バロトロピー流れ」や「等エントロピー流れ」についての解説も加えていきます。

※本記事では、「1次元オイラーの運動方程式」だけを説明します。

スポンサーリンク

目次
  1. 1次元オイラーの運動方程式とは
  2. 1次元の運動量保存則
  3. 右辺の力①②③のについて
    1. 力①について
    2. 力③について
    3. 力②について
    4. 余談ですが・・・・こう考えても同じではないか・・・
  4. 四角形ABCD内の単位時間当たりの運動量変化
  5. まとめると

1次元オイラーの運動方程式とは

式で書くと下記のような偏微分方程式です。

\begin{align*}\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}=-\frac{1}{\rho }\frac{dp}{dx}\end{align*}

これを導出するのが本記事の目標です。

ここには下記の仮定があることを常に意識しなくてはいけません。

【仮定】

  1. 1次元
  2. 非粘性

 

1次元の運動量保存則

今、管内の流れを考えることとします。

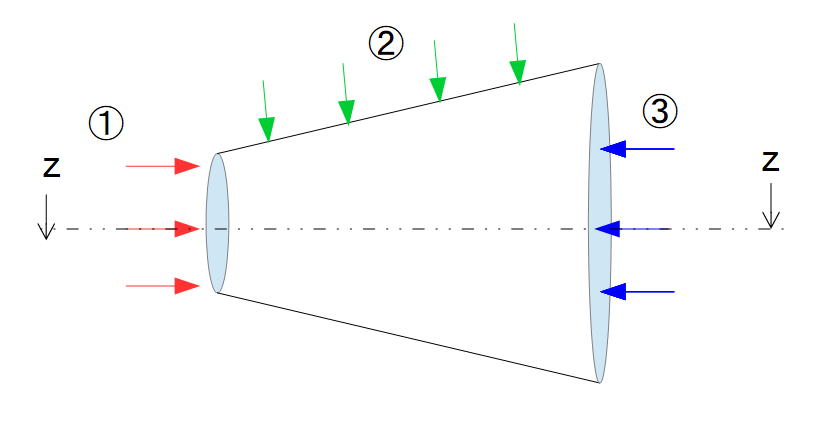
そして下記の絵のように、z-zで断面を切ってできた四角形ABCDについて検査体積を設けて「1次元の運動量保存則」を考えます。

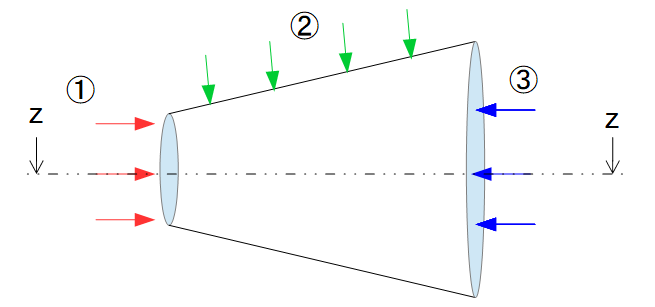
※x軸について、右方向を正としてます。

位置\(x\)における、「表面積を\(A(x)\)」、「圧力を\(p(x)\)」とします。

運動量保存則として、

四角形ABCD内の単位時間当たりの運動量変化＝力①＋力②–力③

を考えれば運動方程式が完成します。

右辺の力①②③のについて

考えやすいものから考えましょう。

力①と力③がx方向に平行な力なので考えやすいため、まずこちらを処理していきます。

※ここでは1次元（x方向のみ）の運動量保存則、すなわち運動方程式を考えていることに注意してください。

力①について

\begin{align*}力①=p(x)A(x)\cdot\cdot\cdot (2)\end{align*}

それぞれ位置\(x\)に依存しているので、\(x\)の関数として記述しておきます。

力③について

\begin{align*}力③=p(x+dx)A(x+dx)\cdot\cdot\cdot (3)\end{align*}

それぞれ微小変化\(dx\)に依存して、圧力と表面積が変化しています。

しかし、それぞれについてテーラー展開すれば、

\begin{align*}(x+dx)=p(x)+\frac{dp}{dx}dx\end{align*}

\begin{align*}A(x+dx)=A(x)+\frac{dA}{dx}dx\end{align*}

となるので、(3)式は、

\begin{align*}力③=p(x+dx)A(x+dx)=p(x)A(x)+p(x)\frac{dA}{dx}dx+A(x)\frac{dp}{dx}dx\cdot\cdot\cdot (4)\end{align*}

となります。

※微小変化\(dx\)についての2次以上の項は無視しました。

力②について

力②については「側面積×圧力」を計算してx方向に分解するということをしなくてはいけないため、非常に計算が面倒です。

側面積×圧力をひとつずつ求めることを考えます。

側面積・・・・

こんな感じで円錐台を展開して側面積を求めても良いでしょう。

そういったときの公式なり考え方については、ネットで色々とありますので、参照していただきたい。

例えば、↓これなど。

http://oto-suu.seesaa.net/article/439870453.html

しかし・・・・求めたいのはx方向の力なので、側面積を求めてx方向に分解するというのは、x方向に射影した面積にかかる力を考えることと同じであります。

だから、下記のような視点から求めた面積（x方向の射影面積)にx方向の圧力を掛ければ、そのままx方向の力になっています。（うまい方法だ(*’▽’)）

これを見ると、求めたい側面のx方向の面積（x方向への射影面積）は、

\begin{align*}A(x+dx)-A(x)=A(x)+\frac{dA}{dx}dx-A(x)=\frac{dA}{dx}dx\cdot\cdot\cdot (5)\end{align*}

となります。

※第一項目と二項目はテーラー展開を使っています。

圧力・・・・

 

圧力についても少し工夫します。

圧力も側面BC(or AD)の間で変化するでしょうが、それは線形に変化しているはずです。

（AB部分での圧力が一番弱く、CD部分での圧力が一番強い・・・としている）

その場合は、側面には全て同じ圧力が均一にかかっているとして、平均的な圧力を代表値にして計算しても求めたい圧力は求めることができます。

平均的な圧力とは、位置\(x+dx\)(ADまでの中間点)での圧力のことです。

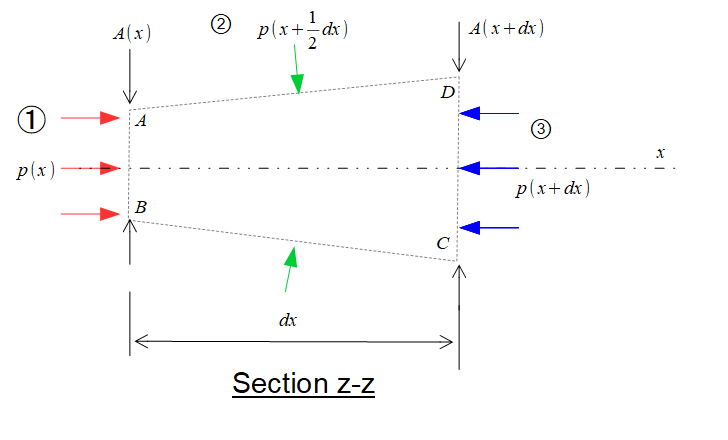
そう考えると、絵のように圧力については、

\begin{align*}p(x+\frac{1}{2}dx)=p(x)+\frac{1}{2}\frac{dp}{dx}dx\cdot\cdot\cdot (6)\end{align*}

を、代表圧力として使うことになります。

力②は・・・

(5)×(6)より、

\begin{align*}\big(p(x)+\frac{1}{2}\frac{dp}{dx}dx\big)\frac{dA}{dx}dx\cdot\cdot\cdot (7)\end{align*}

右辺の力①+②-③

 

右辺①＋②–③＝

\begin{align*}p(x)A(x)\end{align*}

+

\begin{align*}\big(p(x)+\frac{1}{2}\frac{dp}{dx}dx\big)\frac{dA}{dx}dx\end{align*}

–

\begin{align*}\big(p(x)A(x)+p(x)\frac{dA}{dx}dx+A(x)\frac{dp}{dx}dx\big)\end{align*}

\begin{align*}=-\frac{dp}{dx}\,dx\,A・・・(8)\end{align*}

と求まりました。

余談ですが・・・・こう考えても同じではないか・・・

(8)式の結果を見て、わざわざ円錐台を考えましたが、そんなに複雑な形で考える必要があったのか？と思ってしまいました。

太さの変わらない（位置によって面積が変わらない）円管の断面で検査体積を作っても同じ(8)式になるではないかと・・・・

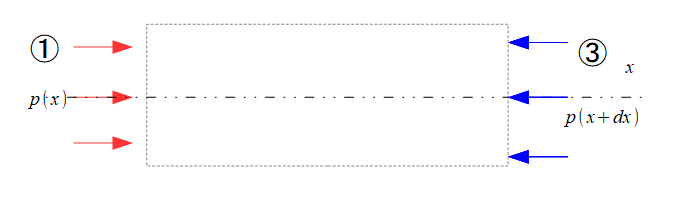
そうすると上で考えた、力②はx方向に垂直な力なので、考えなくても良いことになります。

だから、

\begin{align*}p(x)A-p(x+dx)A=-\frac{dp}{dx}\,dx\,A\cdot\cdot\cdot (9)\end{align*}

と(8)式を一瞬で求めることができました。

いずれにしても円錐台なども形は適当に決めたのですから、シンプルにしたものと同じ結果になるというのは当たり前かという感じですかね。

しかし、円錐台で問題を考えるときは、側面にかかる圧力を忘れてはいけないという良い教訓になりました。

四角形ABCD内の単位時間当たりの運動量変化

運動量変化は質点の場合であれば、

\begin{align*}m\frac{dv}{dt}\end{align*}

と書くでしょうが、流体の場合は少々記述の仕方が変わります。

質点の運動の場合は、座標\(x\)と速度\(v\)は独立な変数として扱っていましたが、流体における流速\(v\)は変数として、位置座標\(x\)と時間\(t\)を変数として持っています。

なので、流体の場合は速度を\(v(x,t)\)と書くことに注意しなくてはいけません。

\begin{align*}\frac{dv}{dt}=\frac{\partial v}{\partial t}+\frac{\partial v}{\partial x}\frac{dx}{dt}\cdot\cdot\cdot (10)\end{align*}

と2変数の微分として考える必要があります。

※↓これとか参考にしてください。

あわせて読みたい

全微分と偏微分の違いを視覚的に理解しておく。

​

(10)式は、\(\frac{dx}{dt}=v\)ですから、

\begin{align*}\frac{dv}{dt}=\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}\cdot\cdot\cdot (11)\end{align*}

となります。

質量については、下記の円錐台の中の質量ですので、

\begin{align*}m=\rho \,dx\,A\cdot\cdot\cdot (12)\end{align*}

となります。

※細かい話をすると円錐台の中の質量は「円錐台の体積×密度」としなくてはいけません。

↓下記の動画を参考にするならば、円錐台の体積は、

https://www.youtube.com/watch?v=FLhOy0XcPNM

と、こんな感じです。

だから今回の場合に適用してみると、

\begin{align*}円錐台の体積=\frac{dx}{3}\big( A(x)+\sqrt{A(x)} \sqrt{A(x+dx)}+A(x+dx)\big)\end{align*}

ですが、\(dx\)はもともとめっちゃくちゃ小さいとしていたとすれば、括弧の中は全て\(A(x)\)だろう。

だから円錐台の体積の体積は、やっぱり

\begin{align*}円錐台の体積=dx\,A(x)\end{align*}

なのです。（少々強引な結論ですが）

まとめると

今まで出てきた結論をまとめてみましょう。

求めたいのが、四角形ABCD内の単位時間当たりの運動量変化＝力①＋力②–力③

これに(8)(11)(12)を当てはめていくと、

\begin{align*}\rho \,dx\,A\big(\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}\big)=-\frac{dp}{dx}\,dx\,A\end{align*}

よって、

\begin{align*}\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}=-\frac{1}{\rho }\frac{dp}{dx}\cdot\cdot\cdot (13)\end{align*}

が導出できました。

これが1次元のオイラーの運動方程式です。

(1)のナビエストークス方程式と比較すると、「1次元（x方向のみ）」「粘性項無し」の流体の運動方程式になります。

冒頭でも説明しましたが、「1次元（x方向のみ）」「粘性項無し（非粘性）」という仮定のもと導出された方程式であることを常に意識しておく必要があります。

この後導出する「ベルヌーイの定理」はこの仮定のもと導出されるものですので、この仮定が適用できない現象に対しては実現象とずれてくることを覚えておかなくてはいけないです。

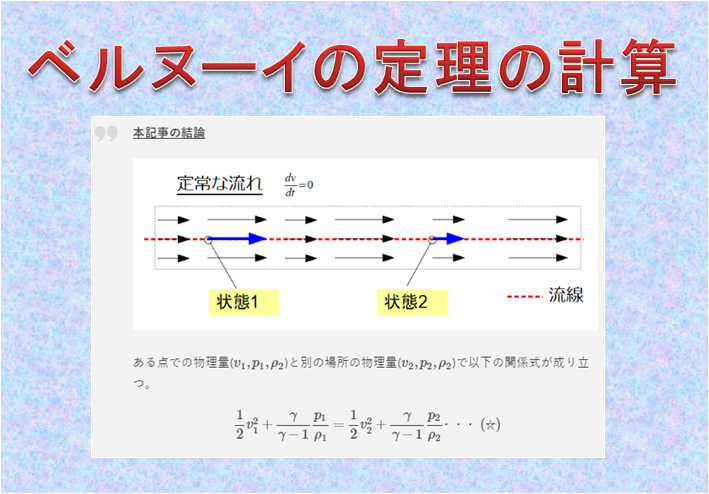
※ベルヌーイの定理はさらに「バロトロピー流れ（等エントロピー流れ）」と「定常流れ（時間に依存しない流れ）」を仮定にしているので、いつでもどんな時でも「ベルヌーイの定理」が成立するからと勘違いして使用してはいけません。

特に間違いやすいのは、ベルヌーイの定理は1次元でのエネルギー保存則になるので、基本的には同じ流線に対してエネルギー保存則が成立するという意味になります。

だからでたらめに選んだ位置同士で成立するものではありません。

そこは注意しなくてはなりません。

関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です