1次元熱伝導方程式の陽解法で解いた時の数値的安定性

こんにちは（@t_kun_kamakiri）(‘◇’)ゞ

たまに数値計算をして・・・時間刻みや空間刻みをどうやって決めれば安定して計算を進めてくれるかなって考えたりします。

（時間刻みはこれくらいだろ！ってやってしまうこともたまにあります・・・ダメなやつだ(*_*;）

そこで、本記事は以下の内容となります。

本記事の内容

数値計算の数値的安定性を考えてみよう(^^)/

※1次元の熱伝導方程式を対象にします。

カマキリ

真面目に考えると面白いよ

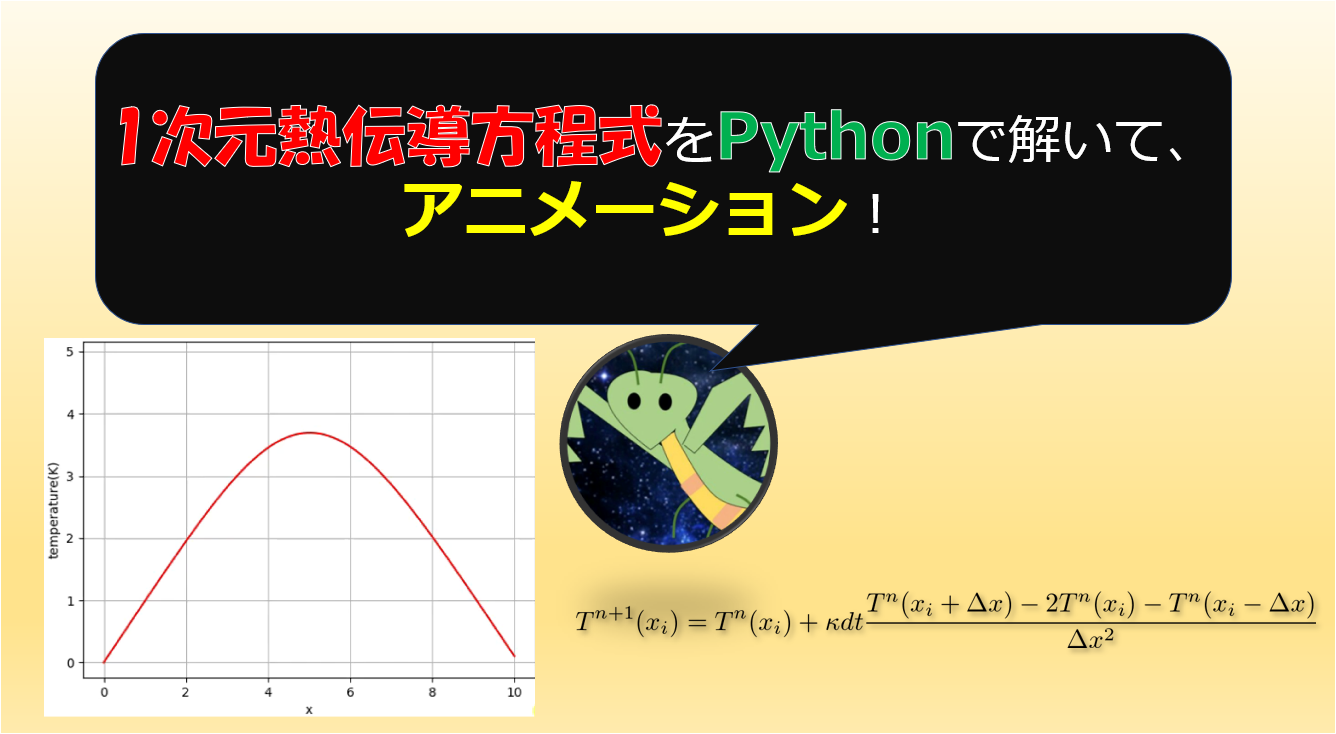
↓こちらの記事を題材にしたいと思います。

前回の記事はこちら

Fortranからgnuplotを使って1次元グラフのアニメーション作成

アニメーションはこんな感じ

カマキリ

前回の記事を読んで遊んでみてください

Fortranからgnuplotを使って1次元グラフのアニメーション作成では、何をやっていたかを簡単におさらいしておきます。

以下の1次元の熱伝導方程式

1次元熱伝導方程式

\begin{align*}\frac{\partial T}{\partial t}=\kappa\frac{\partial^2T}{\partial^2 x}\tag{1}\end{align*}

を次のようにして離散化して解きました。

ある地点\(x_{i}\)での時間微分の項

\begin{align*}\frac{\partial T}{\partial t}\simeq \frac{T^{n+1}(x_{i})-T^{n}(x_{i})}{\Delta t}\end{align*}

微分を差分に置き換えただけです。

数値計算では時間をステップ数で数えるため、時間変数の代わりにステップ\(n\)として文字の頭に添えています。

ある時間\(t\)での空間微分の項

\begin{align*}\kappa\frac{\partial^2T}{\partial^2 x}\simeq \kappa\frac{T^{n}(x_{i}+\Delta x)-2T^{n}(x_{i})-T^{n}(x_{i}-\Delta x)}{\Delta x^2}\end{align*}

これは空間に対して2次の精度となります。

よって、(1)式を離散化してものは次のようになります。

\begin{align*}T^{n+1}(x_{i})=T^{n}(x_{i})+\kappa dt\frac{T^{n}(x_{i}+\Delta x)-2T^{n}(x_{i})-T^{n}(x_{i}-\Delta x)}{\Delta x^2}\tag{2}\end{align*}

このような方程式に限らず、解析解が見つかっていないような偏微分方程式を数値的に解く場合があると思います。

精度：いかに元の方程式を忠実に解いているか？
安定性：いかに安定して方程式を解いているか？

以上の2点はとても重要です。

今回は、(2)式のような1次元熱伝導方程式を時間に対して陽解法で解いた場合の数値的安定性について解説しようと思います(^^)/

オイラー陽解法
1次元熱伝導方程式のオイラー陽解法の安定性について
数値的に不安定な状況とは
ノイマンの安定性解析
1. (6)式を(4)式に代入して振幅\(A^{n}_{k}\)が大きくならないような条件を導こう
まとめ

オイラー陽解法

\begin{align*}T^{n+1}(x_{i})=T^{n}(x_{i})+\kappa dt\frac{T^{n}(x_{i}+\Delta x)-2T^{n}(x_{i})-T^{n}(x_{i}-\Delta x)}{\Delta x^2}\tag{2}\end{align*}

のように、右辺を\(n\)時刻の変数の形にして表す離散化解法をオイラー陽解法といいます。

もともと時間微分に対して、1次精度で単純な差分の形に近似しているため、(2)式では直接\(n+1\)時刻の温度場を求めることができるのです。

とてもシンプルな数値的解法ではありますが、(2)式を式変形すると数値的に不安定な面が見えてきます。

1次元熱伝導方程式のオイラー陽解法の安定性について

※以降、\(T^{n}(x_{i})=T^{n}_{i}\)と書くこととします。

\begin{align*}T^{n+1}_{i}=T^{n}_{i}+\kappa dt\frac{T^{n}_{i+1}-2T^{n}_{i}-T^{n}_{i-1}}{\Delta x^2}\tag{3}\end{align*}

これを、式変形します。

\begin{align*}
T^{n+1}_{i}=cT^{n}_{i+1}+(1-2c)T^{n}_{i}+cT^{n}_{i-1}\tag{4}
\end{align*}

※\(c=\frac{\kappa\Delta t}{\Delta x^2}\)と置きました。

(4)式を眺めると、\(1-2c<0\)だと温度分布によっては、ある時刻で温度が負の値になるようなこともあるかなーーーってことに気付きます。

数値的に安定に解いてくれるためには、\(1-2c\geq 0\)という条件が必要なのではないかなという気がするのです。

カマキリ

気がするだけではいけないので、次の章で示してみましょう

ひとまずここまでで、

(4)式の数値的な安定性条件

\begin{align*}
c\leq \frac{1}{2}\tag{5}
\end{align*}

こうかな？
というところまでわかりました。

数値的に不安定な状況とは

数値的に不安定である解法ってどういう状況のことでしょうか・・・

不安定な状況とは、はじめはおとなしい波を立てていたのに、時間が経つと振幅が大きい荒々しい波になってしまうような状況のことです。

つまり、関数を波に分解したときに波が時間が経つにつれて増大してしまう状況が、数値的に不安定な状況であると言えます。

それが偏微分方程式を離散化したときに起こってしまっては困るのです(‘_’)

逆に、波の振幅が大きくてなってしまうような要因を数値解法の中に入っていないことが、安定性のポイントになるのです。

カマキリ

・・・ということをつい最近学びました。

ノイマンの安定性解析

数値的に不安定な状況というのが何となく理解したところで、以下に数値的な安定性を調べる方法のポイントを整理しておきます。

ポイント

関数を波に分解→フーリエ変換（or フーリエ級数展開）
時間が経つと波の振幅が大きくなる（大きくなると不安定）

このようなポイントで数値解の安定性を解析する方法を、ノイマンの安定性解析といいます。

フーリエ変換は下記のようにある関数\(f(x)\)を、\(\sin\)波や\(\cos\)波や正弦波\(e^{ikx}\)などの様々な異なる波数の波に分解して波の空間（波数空間）に変換する方法のことです。

どんな関数も異なる波数の\(\sin\)波の和で書いてやるのです。↓こんな感じです。
※以下の場合は周期関数\(f(x)\)に関して、例を挙げています。

こうやって考えると、「おや？\(\sin2\pi x\)(周期１)の波が1個か・・・・\(\sin10\pi x\)(周期１/10)の波が10個か・・・」と、波のくせに数えれるという恩恵を受けることができます。

「1個、10個、3個」とか書いたものがフーリエ変換（or フーリエ級数展開）した後の関数（波数空間での関数）のこと
「1個、10個、3個」は各波数の波の振幅

と考えることができます。

カマキリ

↑上の説明はフーリエ変換というよりは、フーリエ級数展開したときの解説でありますが、似たようなものです（離散的か連続、周期関数か非周期関数かの違い）

数値的に不安定な解とはこういうことです。

「1個、10個、3個」などと書いた各波数の波の振幅が時間が経つにつれて、どんどん大きくなってしまう場合が不安定な数値解であるということです。

温度場の関数をフーリエ級数展開して記述するのであればあれば、

\begin{align*}
T(x,t)=\sum A(k,t)e^{Ikx}\tag{5}
\end{align*}

これを、時刻\(n\)ステップと格子点\(i\)で書き換えます。

\begin{align*}
T(x,t)=\sum A^{n}_{k}e^{Ik(i\Delta x)}\tag{6}
\end{align*}

※虚数は\(I\)、格子点は\(i\)と書いています。紛らわしいですが・・・
ちなみに\(\sum\)は波数\(k\)についての和です。
\(\Delta x\)は離散化した際の格子幅です。

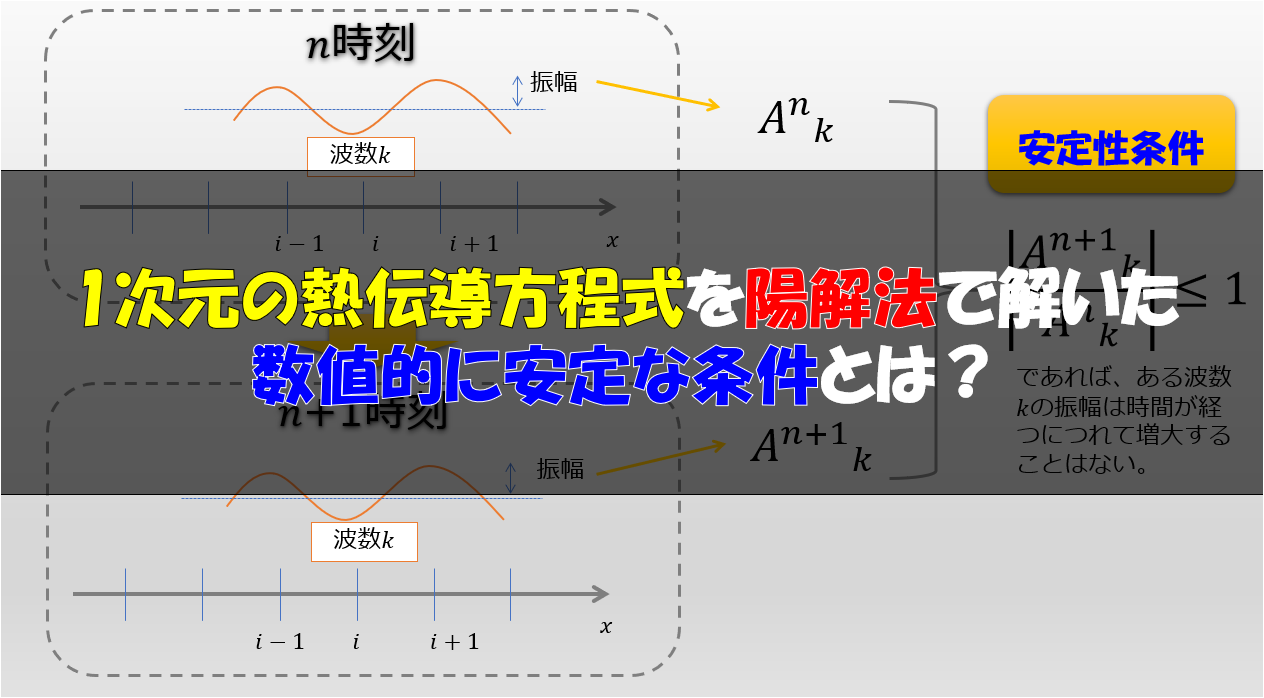
数値的に安定とは、ある時刻\(n\)でのある格子点\(i\)の波数を考えた時に\(n+1\)時刻で増幅してしまう様な答えを導かないということです。

つまり、↓こんな感じ。

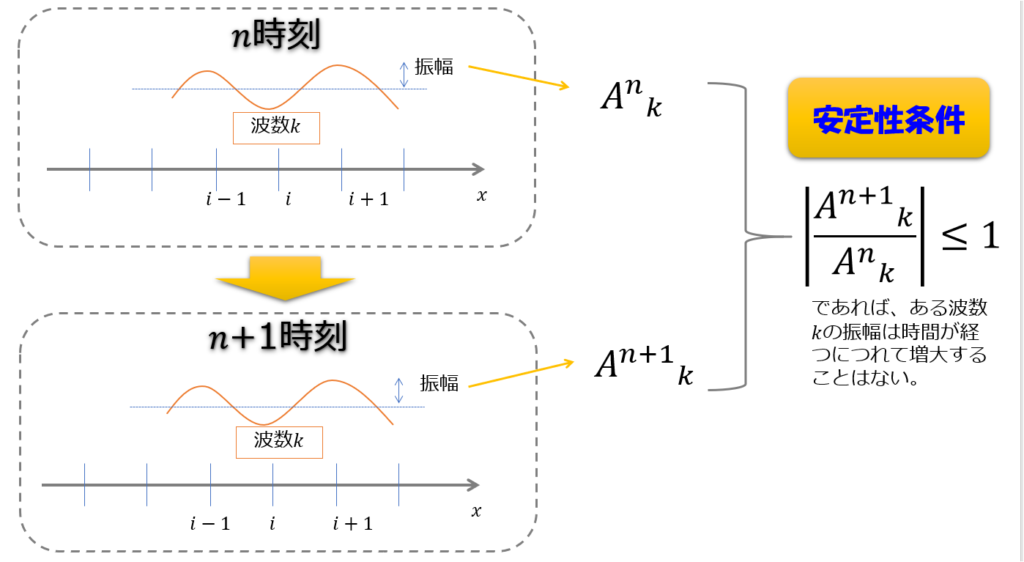
(6)式を(4)式に代入して振幅\(A^{n}_{k}\)が大きくならないような条件を導こう

(6)式を(4)式に代入するわけですが、元々の1次元の熱伝導方程式は線形の方程式であるので、各波数ごとに方程式が成り立ります。

だから、ある波数\(k\)についてのみ考えれば十分であるので、\(\sum\)はとっぱらって考えることにします。

では、(6)式を(4)式に代入してみます。

\begin{align*}
A^{n+1}_{k}e^{Ik\Delta x i}=cA^{n}_{k}e^{Ik\Delta x (i+1)}+(1-2c)A^{n}_{k}e^{Ik\Delta x i}+A^{n}_{k}e^{Ik\Delta x (i-1)}\tag{7}
\end{align*}

両辺を\(A^{n}_{k}e^{Ik\Delta x i}\)で割って、\(e^{i\theta}=\cos(\theta)+i\sin(\theta)\)を使いつつ整理すると・・・

\begin{align*}
\frac{A^{n+1}_{k}}{A^{n}_{k}}=1+2c\big(\cos(k\Delta x)-1\big)\tag{8}
\end{align*}

となります。

ここで数値的に安定であるためには、

各波数の振幅が時間とともに増幅していってはいけない\(\left|\frac{A^{n+1}_{k}}{A^{n}_{k}}\right|\leq 1\)ということなので、

\begin{align*}
-1\leq 1+2c\big(\cos(k\Delta x)-1\big)\leq 1\tag{9}
\end{align*}

が安定性の条件です。

ただ、コサイン自体が\(-1\leq \cos(k\Delta x)\leq 1\)という範囲に制限されているので、\(c\)にも条件が出てきそうであることがわかります。

安定な数値解を得るためにはどのような波数\(k\)であっても、不等式(9)を満たしておく必要があるということです。

上限について
\(1+2c\big(\cos(k\Delta x)-1\big)\)が最も1を超えそうな状況とは、\(\cos(k\Delta x)=1\)の時です。
\(\cos(k\Delta x)=1\)のときにも不等式(9)に入っているための\(c\)である必要がありますが、この場合には\(c\)が消えてしまいます。
ゆえに、どんな場合でも(9)式の上限側は成り立つことがわかります。
下限について
\(1+2c\big(\cos(k\Delta x)-1\big)\)が最も-1を下回りそうな状況とは、\(\cos(k\Delta x)=-1\)の時です。
\(\cos(k\Delta x)=-1\)のときでも、不等式(9)に入っているための\(c\)である必要があります。

この不等式の「下限」の条件から、\(c\)の条件が決まります。

\begin{align*}
c\leq \frac{1}{2}\tag{10}
\end{align*}

これが各波数の振幅が時間とともに増幅していってはいけないという条件です。

つまり不等式(10)が数値的に安定な条件ということになります。

カマキリ

(5)式と同じ結果が得られた