こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
比熱の温度依存性について勉強しています。
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
必要とする前提知識
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の記事のまとめ
前回の記事の内容を軽くおさらいしておきましょう。
「3次元(空間)、粒子数N個」でのハミルトニアン
から、準古典近似での分配関数を計算しました。
Z = \frac{1}{(2\pi\hbar)^{3N}}\Pi_{i}^{N}\bigg(2m_{i}k_{B}T\bigg)^{\frac{3}{2}}\bigg(\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{(i)}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg)
\end{align*}
理想気体の2原子分子の分配関数を計算する
ここまでは、3次元(空間)、粒子数N個の古典近似での分配関数を求めました。
Z &= \frac{1}{N!(2\pi\hbar)^{3N}}\bigg(2m_{i}k_{B}T\bigg)^{\frac{3N}{2}}\Pi_{i}^{N}\bigg(\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{(i)}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg) \\
&= \frac{1}{N!}\bigg(\frac{mk_{B}T}{2\pi\hbar^2}\bigg)^{\frac{3N}{2}}\Pi_{i}^{N}\bigg(\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{(i)}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg)
\tag{17}
\end{align*}
※N個の粒子は区別できないため、N!通り余分にカウントしているためN!で割っています。
ここからは、2原子分子がN個存在する場合を考えます。
(原子数:2N個)
今回考えているのはHCl、CO、NOなどの異なる2原子から成る分子を想定しています。
しかし、今考えようとしているのは理想気体ですので、分子と分子間の相互作用は考慮しないことになります。
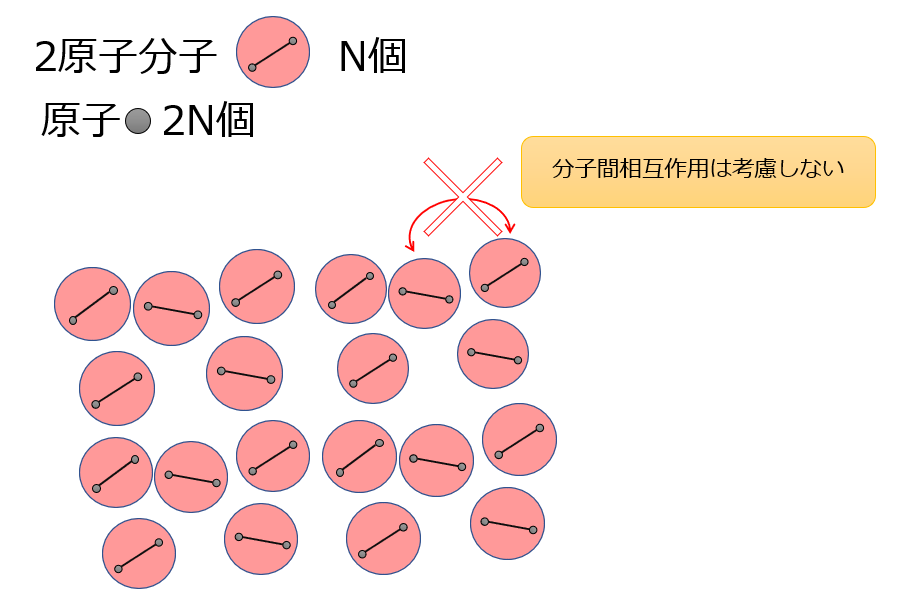

つまり、N個の2原子分子は相互作用を及ぼさずに独立に運動することになりますので、分配関数は2原子分子のみを考えることにします。
2N個の2原子分子を考えるときは、2原子分子の分配関数をN回掛ければ良い(N乗)ということになります。
2原子分子1個の分配関数
ハミルトニアンは、
H=\frac{|\boldsymbol{p^{(1)}}|^2}{2m_{1}}+\frac{|\boldsymbol{p^{(2)}}|^2}{2m_{2}}+V(q)
\end{align*}
※\(q\)は2原子間の中心間の距離:\(q=|\boldsymbol{q^{(1)}}-\boldsymbol{q^{(2)}}|\)
- 2原子分子なので\(N=2\)
- 相互作用\(V(q)\)は2原子間なので1つだけ
です。
次式を計算していきます。
Z &=\frac{1}{(2\pi\hbar)^{2\times 3}}\bigg(2m_1 K_B T\bigg)^{\frac{3}{2}}\bigg(2m_2 K_B T\bigg)^{\frac{3}{2}}\bigg(\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{i}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg) \\
&= Z_1 Z_2\tag{2}
\end{align*}
Z_1=\frac{1}{(2\pi\hbar)^{2\times 3}}\bigg(2m_1 K_B T\bigg)^{\frac{3}{2}}\bigg(2m_2 K_B T\bigg)^{\frac{3}{2}}
\end{align*}
Z_2=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{i}}\})}{k_B T}}d\boldsymbol{q^{(i)}}
\end{align*}
※今回は分子内の2つの原子は区別できるものとしているため、2!で割る必要はありません。
(2)式は、運動量に関する積分(運動エネルギーの部分)の分配関数\(Z_1\)と、座標に関する積分(相互作用エネルギーの部分)の分配関数\(Z_2\)とにきれいに分離して計算できることがわかります。
ところで、(2)式は相互作用ポテンシャルの形によって分配関数\(Z_2\)の結果が変わってきますよね。
つまり、相互作用ポテンシャルがどのようなモデルで記述するかによって分配関数\(Z\)結果が変わってくるということです。
では、関心ごとは以下(3)式を計算することにあります。
Z_2=\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{i}}\})}{k_B T}}d\boldsymbol{q^{(i)}}
\tag{3}
\end{align*}
ここでは、2原子分子の2原子間には以下の相互作用ポテンシャルがはたらいているとします。
- 原子間距離が近い場合は強い斥力がはたらく
- 原子間距離が遠い場合は弱い引力がはたらく
これはモデルはバネの振動をイメージする場合と同じですね。
以上のようなポテンシャル\(V(\{\boldsymbol{q^{i}}\})\)はおおよそ下記のようなポテンシャルの形になります。
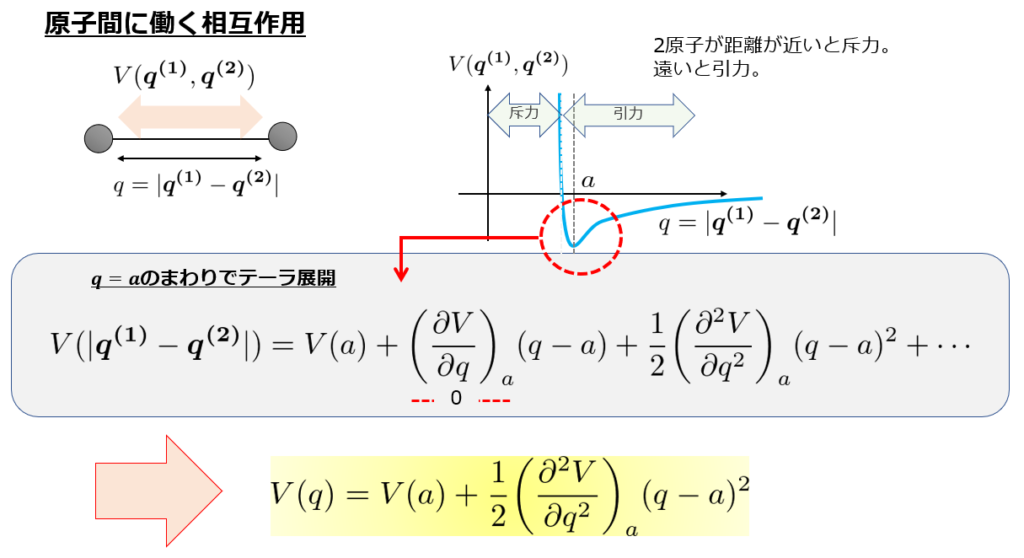

ここで、2原子の距離はほぼ一定であるとします。
そのとき、ポテンシャルの底(2原子間距離\(q\)が\(a\)のとき)のまわりで安定して実在していると考えられます。
また、ポテンシャルと基準点は物理的にはあまり意味を持たないので、\(V(a)=0\)としておきます。
V(q)=\frac{1}{2}\kappa (q-a)^2
\end{align*}
\(\kappa=\frac{\partial^2 V}{\partial q^2}\)と置きました。
結局ハミルトニアンを、
H=\frac{|\boldsymbol{p^{(1)}}|^2}{2m_{1}}+\frac{|\boldsymbol{p^{(2)}}|^2}{2m_{2}}+\frac{1}{2}\kappa (q-a)^2
\end{align*}
として分配関数を計算しているという認識をしておきましょう(^^)/
ここでは、\(q=a\)より離れると急激にポテンシャルが大きくなるようなモデルを想定していますので、\(\kappa\)がとても大きな値を持っているとします。
すると、(19)式は極座標表示で積分すると、
\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{i}}\})}{k_B T}}d\boldsymbol{q^{(i)}}=\int^{\infty}_{0}4\pi q^2 e^{-\frac{\kappa (q-a)^2}{2k_B T}}dq
\tag{4}
\end{align*}
となります。
(4)式の積分を考えていくのですが、少し近似しながら積分することにします。
今、相互作用ポテンシャルを下記のように安定している部分(\(q=a\))のまわりをテーラー展開して2次関数で近似しました。


ですので、\(\int^{\infty}_{0}4\pi q^2e^{\frac{\kappa(q-a)}{2k_B T}}dq\)の積分の計算において、
被積分関数は\(q=a\)のまわりにしか寄与していないと近似し以下の操作をすることで積分が実行出ます。
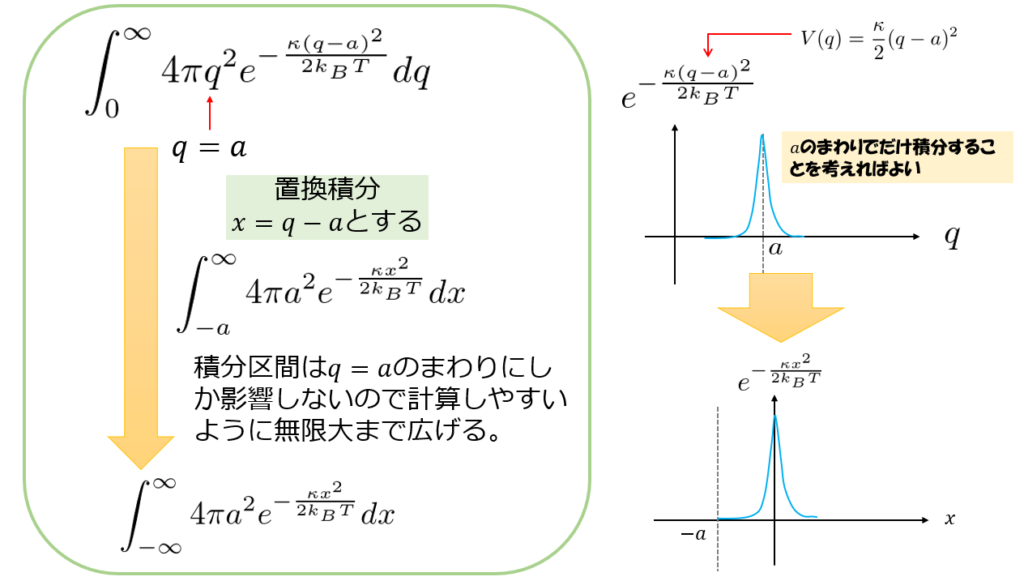

ここで再びガウス積分の公式を使うことにより、(4)式は近似的に
(4)\simeq \int^{\infty}_{-\infty}4\pi a^2 e^{-\frac{\kappa x^2}{2k_B T}}dq=4\pi a^2\sqrt{2\pi\kappa k_B T}\tag{5}
\end{align*}
と計算できます。
よって(2)式が、
Z =\bigg(\frac{m_1 k_{B}T}{2\pi\hbar^2}\bigg)^{\frac{3}{2}}\bigg(\frac{m_2 k_{B}T}{2\pi\hbar^2}\bigg)^{\frac{3}{2}}4\pi a^2\sqrt{2\pi\kappa k_B T}\tag{6}
\end{align*}
分配関数の温度のべき乗はエネルギーの2次関数の数と関係している
実は分配関数の温度のべき乗というのは、エネルギーを2次関数で書いた時の数と関係していることがわかります。
例えば、
- 運動エネルギーは運動量の2次関数であり、自由度\(f\)とすれば、
\begin{align*}K=\sum_{i=1}^{f}\alpha_{i}^2p_{i}^2\end{align*}
と表される場合、分配関数\(Z\)の温度は\(\frac{f}{2}\)乗となり、比熱は\(\frac{f}{2}k_B\)となる。
また、
- 相互作用ポテンシャルエネルギーが位置の2次関数であり、自由度\(f\)とすれば、
\begin{align*}K=\sum_{i=1}^{f}\alpha_{i}^2r_{i}^2\end{align*}
と表される場合、分配関数\(Z\)の温度は\(\frac{f}{2}\)乗となり、比熱は\(\frac{f}{2}k_B\)となる。
つまり先ほどの例では、
運動量の2次関数が3×2=6個、位置の2次関数が1個だったので、分配関数の温度は\(\frac{7}{2}\)乗だったというわけです。
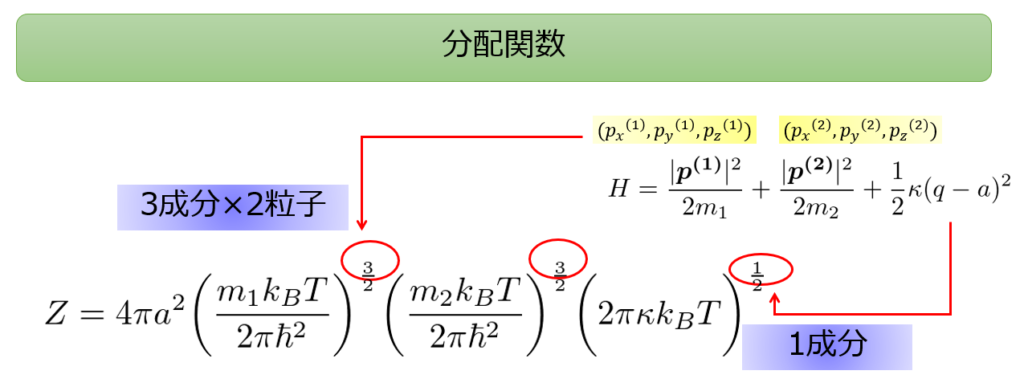

このことが比熱\(c\)の値と深く関係しています。
運動量と位置の2次関数の数が\(f\)個あれば、比熱が\(c=\frac{7}{2}k_B\)となるわけです。
本当にそうなるのかを分配関数\(Z\)から比熱を計算してみましょう。
比熱はエネルギーの期待値を温度で微分すれば求まるので、まずはエネルギーの期待値を求めてみましょう。
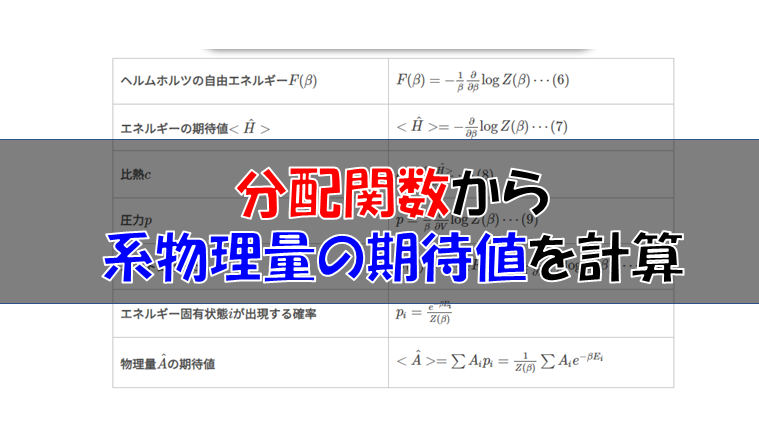
| ヘルムホルツの自由エネルギー\(F(\beta)\) | \(F(\beta)=-\frac{1}{\beta}\log Z(\beta)\cdots (6)\) |
| エネルギーの期待値\(<\hat{H}>\) | \(<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)\cdots (7)\) |
| 比熱\(c\) | \(c=\frac{\partial <\hat{H}>}{\partial T}\cdots (8)\) |
| 圧力\(p\) | \(p=-\frac{\partial F}{\partial V}=\frac{1}{\beta}\frac{\partial}{\partial V}\log Z(\beta)\cdots (9)\) |
| エントロピー\(S\) | \(S(\beta)=-\frac{\partial}{\partial T}F(\beta)\cdots (10)\) |
| エネルギー固有状態\(i\)が出現する確率 | \(p_{i}=\frac{e^{-\beta E_{i}}}{Z(\beta)}\) |
| 物理量\(\hat{A}\)の期待値 | \(<\hat{A}>=\sum A_{i}p_{i}=\frac{1}{Z(\beta)}\sum A_{i}e^{-\beta E_{i}}\) |
分配関数を知るとこれだけの物理量が計算できるのですから、とても便利なものだなという印象を持ってもらえたかと思います。
エネルギーの期待値
<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)\tag{7}
\end{align*}
分配関数の係数部分は\(A\)とおいてまとめて、計算しやすいように\(\beta=\frac{1}{k_B T}\)と置いておきます。
Z =A\bigg(k_B T\bigg)^{\frac{7}{2}}=A\beta^{-\frac{7}{2}}
\end{align*}
これを(7)式に代入すると、
<\hat{H}>=-\frac{\partial }{\partial \beta}\bigg(\log A+ \log \beta^{-\frac{7}{2}}\bigg)=\frac{7}{2}k_B T
\end{align*}
となります。
よって、比熱\(c=\frac{\partial }{\partial T}<\hat{H}>\)は、
c=\frac{7}{2} k_B\tag{8}
\end{align*}
となります。
これにて、
2原子分子の比熱が求まりました!
しかし、実はこれは実験値とあまり良い一致を示ていないということがわかっています。
それは次の点で一致をしていないということです。
- 2原子分子の比熱は\(\frac{5}{2}k_B \)に近い
- 比熱は温度の広い範囲で一定値であるが、温度依存性を持っている
この問題に対する答えは本記事の「古典力学」の範疇では答えることができません。
この比熱の問題はマクスウェルもボルツマンも随分悩まされたようです。
解決するために「量子力学」の知識を使わなければならないということがわかっています。
まとめ
今まで行った流れをおさわいしておきましょう。
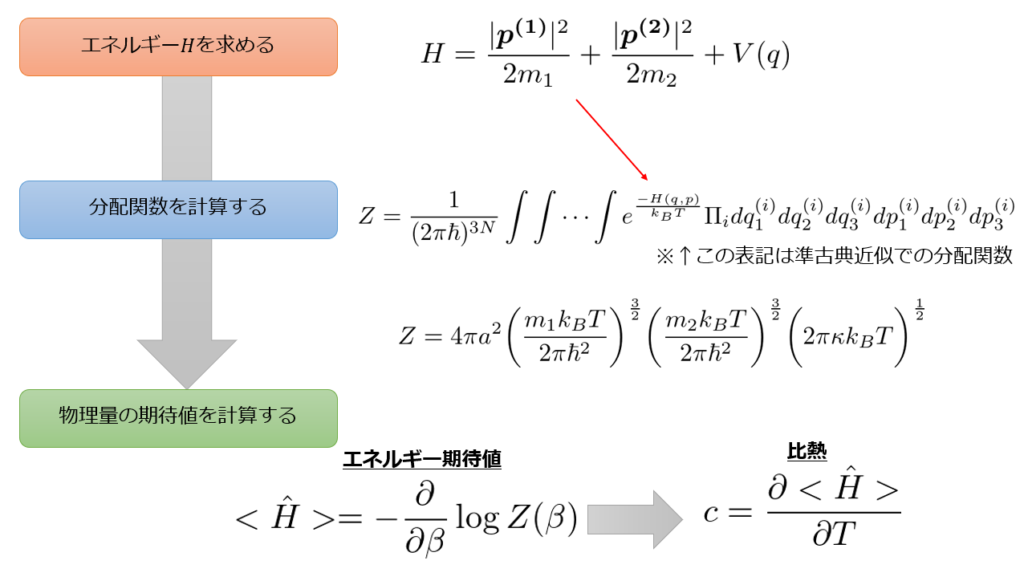

以上の流れで「古典近似における2原子分子の比熱」が計算できました。
※実はこの「2原子分子の比熱」は実験値とは一致していません。
以下の2点が実験事実です。
- 2原子分子の比熱は\(\frac{5}{2}k_B T\)に近い
- 比熱は温度の広い範囲で一定値であるが、温度依存性を持っている
この2点は「古典力学」の範疇では答えることができません。
本記事の冒頭で書いた文章をもう一度記載しておきます!