こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
「比熱の温度依存性の理解のため」のための記事です。
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
必要とする前提知識
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の記事のまとめ
まずは前回の記事のおさらいをしていきます。
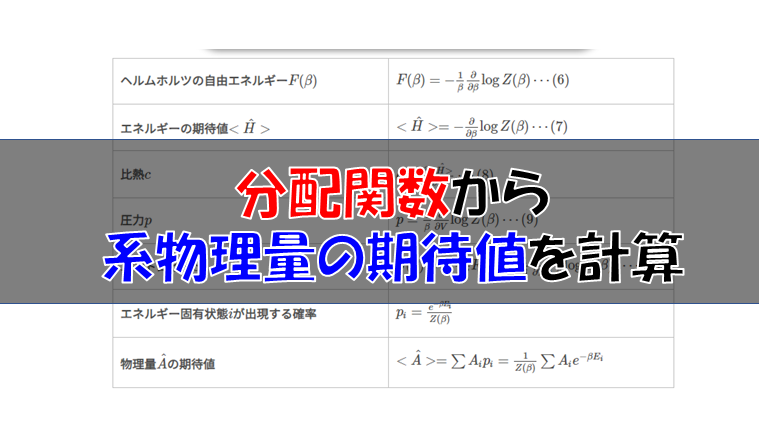
カノニカル分布での分配関数
| ヘルムホルツの自由エネルギー\(F(\beta)\) | \(F(\beta)=-\frac{1}{\beta}\log Z(\beta)\cdots (6)\) |
| エネルギーの期待値\(<\hat{H}>\) | \(<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)\cdots (7)\) |
| 比熱\(c\) | \(c=\frac{\partial <\hat{H}>}{\partial T}\cdots (8)\) |
| 圧力\(p\) | \(p=-\frac{\partial F}{\partial V}=\frac{1}{\beta}\frac{\partial}{\partial V}\log Z(\beta)\cdots (9)\) |
| エントロピー\(S\) | \(S(\beta)=-\frac{\partial}{\partial T}F(\beta)\cdots (10)\) |
| エネルギー固有状態\(i\)が出現する確率 | \(p_{i}=\frac{e^{-\beta E_{i}}}{Z(\beta)}\) |
| 物理量\(\hat{A}\)の期待値 | \(<\hat{A}>=\sum A_{i}p_{i}=\frac{1}{Z(\beta)}\sum A_{i}e^{-\beta E_{i}}\) |
分配関数を知るとこれだけの物理量が計算できるのですから、とても便利なものだなという印象を持ってもらえたかと思います。
カノニカル分布の準古典近似
温度\(T\)(平衡状態)でのカノニカル分布を準古典近似で表現したいと思います。
量子力学での世界では粒子のもつエネルギーというのはとびとびでありますが、本記事では量子力学を用いない古典的な取り扱いをする場合の計算方法について考えていきたいと思います。
※まずは簡単に考えるために、1次元の1粒子として考えます。
カノニカル分布の和を積分に変える
1次元、1粒子
量子力学での取り扱いでは、エネルギー準位は{\(E_{1},E_{2},E_{3},\cdots\)}のようにとびとびの値をとっていました。
ですのでカノニカル分布を考えて、量子力学を考慮した場合の分配関数は、
カノニカル分布での分配関数
のように和の形で書いたのです。
しかし、とびとびのエネルギー準位\(\Delta E<<k_{B}T\)であるような高温状態であるとき、\(\Delta E=E_{n}-E_{n-1}\)の幅はほとんど気にならなくなります。
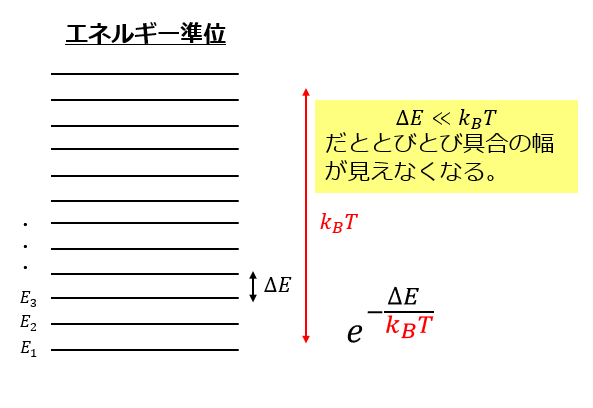

エネルギー準位のとびとび具合が気にならなくなるということは、幅は無限に小さいと考えてよいということになります。
つまり、エネルギー準位は連続になるので、分配関数の和は積分に変えることができます。
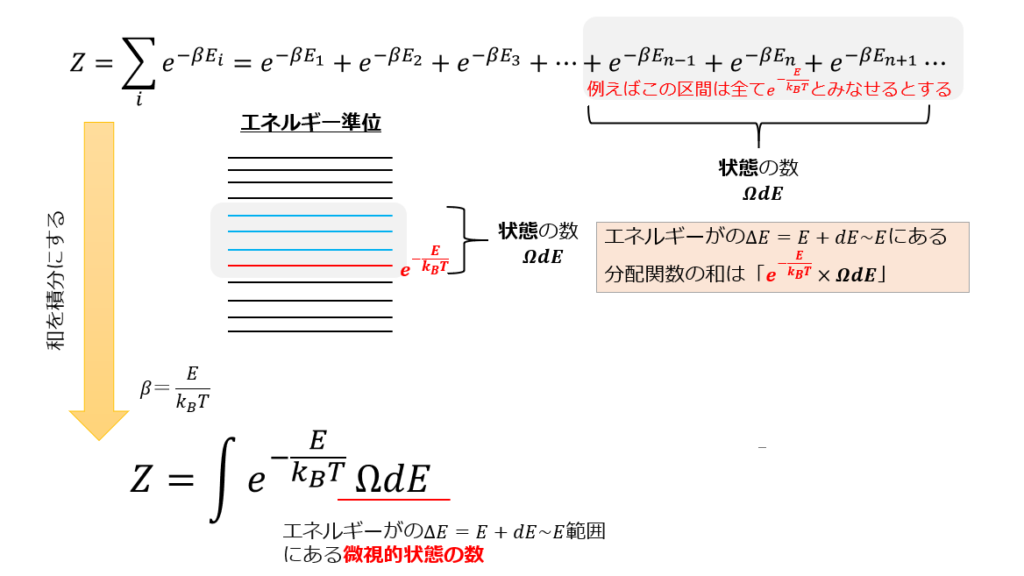

和から積分に変えるときに「\(\Delta E=E\sim E+dE\)の間にある微視的な状態」は全て\(e^{-E/k_{B}T}\)と考え、\(E\sim E+dE\)の中にある状態数が\(\Omega (E)\)個あるすると、\(E\sim E+dE\)の中にある分配関数は、
と書けます。
それを全てのエネルギーで足し合わせる(積分)と、分配関数となります。
微視的な状態の数(状態数)\(\Omega (E)\)をどう考えるか?
次に、微視的な状態の数(状態数)\Omega (E)を、準古典近似でどのように書けるかを考えていくことにします。
状態数は、位相空間(「横軸:位置\(q\)、縦軸:運動量\(p\)」の空間)での「状態の数」をカウントすれば良いです。
だから、状態数というのは位相空間で考えると「1個の量子状態が存在する最小面積\(\Delta q\Delta p\)」を単位として、
状態数=全体の面積/最小単位の面積
これで状態数を計算すればよいです。
絵で書くとこんな感じです(^^)
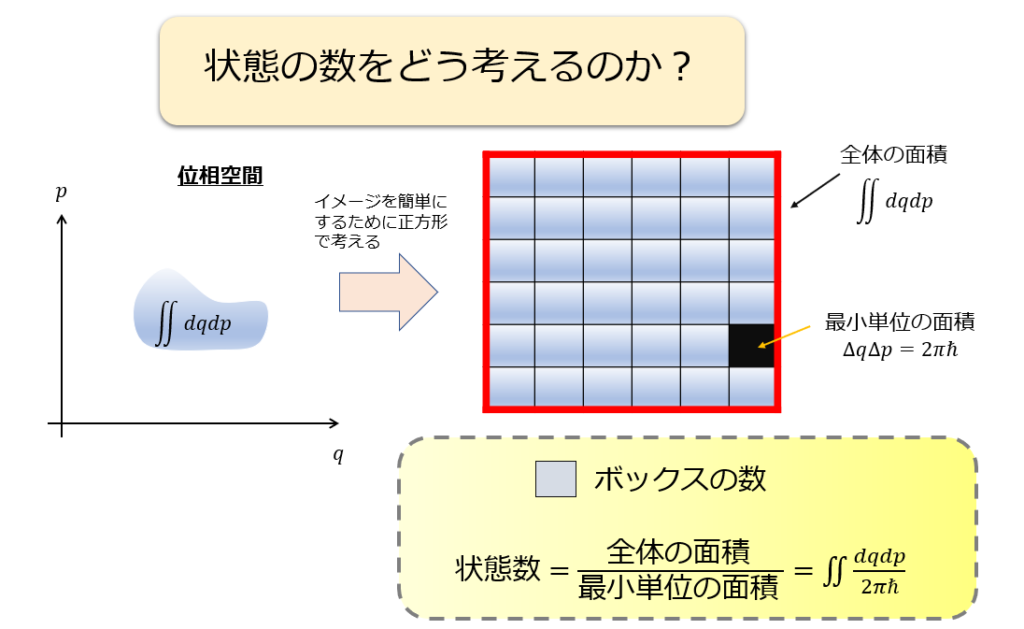

※ここではエネルギー\(H(q,p)\)(ハミルトニアン)と書くことにします。
よって、1次元1粒子の運動による分配関数は、
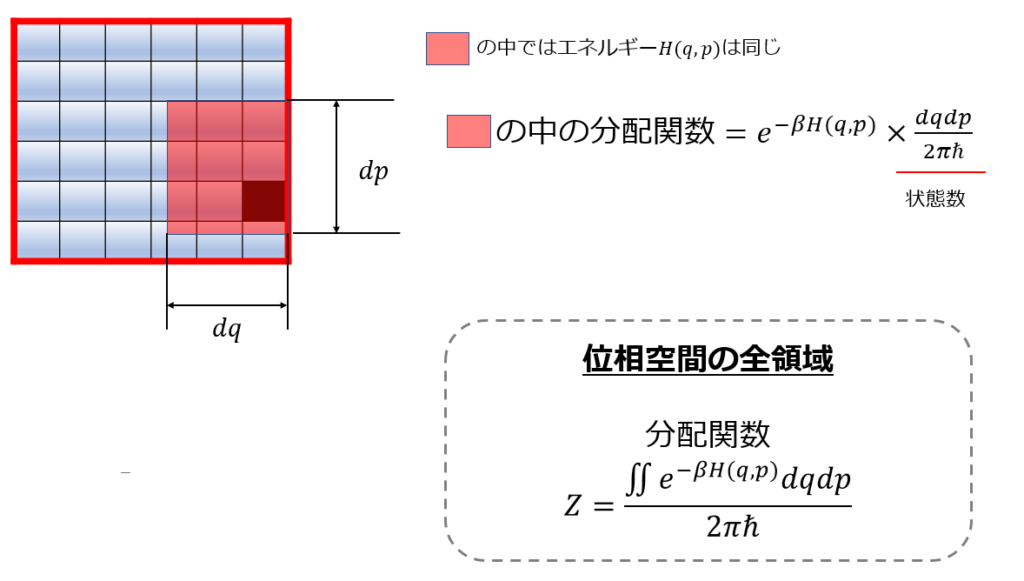

となります。
3次元(3次元空間)、粒子数N個
1次元、1粒子の分配関数をヒントに「3次元空間の粒子数N個」における分配関数への拡張は容易となります。
分配関数は、
となります。
\(N!\)で割っているのは、N個の粒子は同じ粒子として考える必要があるため、粒子の入れ替えに対しては\(N!\)通りあり、そのため状態数としてカウントしすぎている分を考慮して割っているのです。
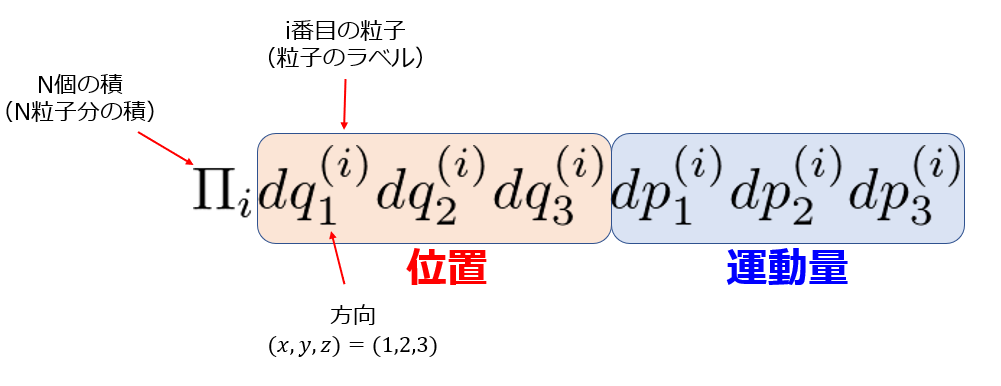
積分の数がとても多いですが、添え字の意味は下記のようになります。

(11)式を見ると、ハミルトニアン\(H(q,p)\)がわかれば分配関数\(Z\)がわかるということになります。
ハミルトニアンを考えて、分配関数を計算
まずは一般的な話をするために、「3次元(空間)のN粒子」について考えることにします。
その後に、「3次元(空間)の2原子分子」の分配関数を考える流れで説明していきます。
「3次元(空間)、粒子数N個」でのハミルトニアン
ここでは計算をしやすくするために、粒子にいったんラベル付けして区別しておくようにしておきますが、今考えている粒子は全て同じ粒子であることに注意しておきます。
H({q^{(1)}_{1},q^{(1)}_{2},q^{(1)}_{3},q^{(2)}_{1},q^{(2)}_{2},q^{(2)}_{3},\cdots,p^{(1)}_{1},p^{(1)}_{2},p^{(1)}_{3},p^{(2)}_{1},p^{(2)}_{2},p^{(2)}_{3},\cdots,})\end{align*}
のような書き方では、とても長くなってしまうので、以下のように表記します。
- ベクトル表記は太字:\(\boldsymbol{q^{(i)}}=(q^{(i)}_{1},q^{(i)}_{2},q^{(i)}_{3})\)
※\((1,2,3)=(x,y,z)\) - 頭についている添え字\(\boldsymbol{q^{(i)}}\)は\(i\)番目の粒子(ラベル)
- 各原子の質量を\(m_i\)
ハミルトニアンは、
となります。
(4)式を分配関数\(Z\)に代入して、計算を進めていくことになります。
流れは下記のような感じです。
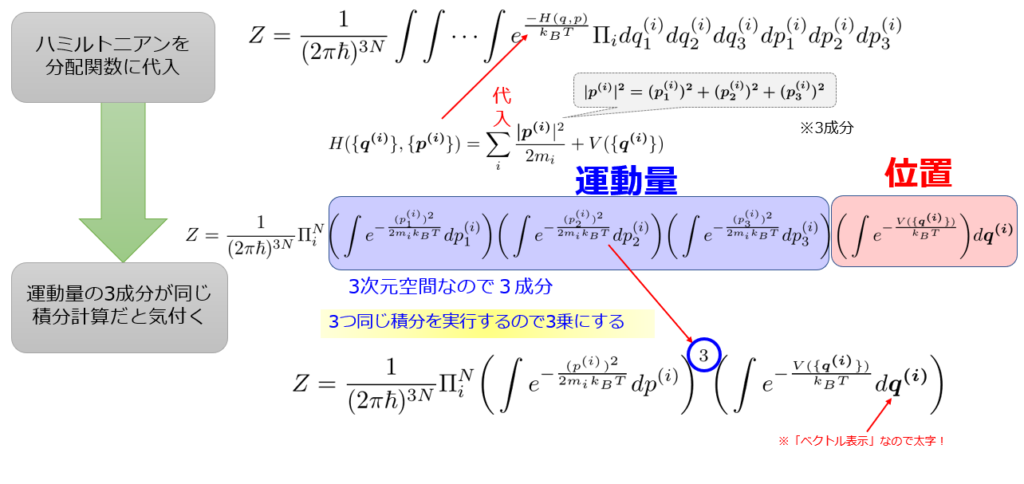

上の流れに沿ってまとめていくとこのようになります。
積分区間もちゃんと書いてあげて・・・
Z =\frac{1}{(2\pi\hbar)^{3N}}\Pi_{i}^{N}\bigg(\int^{\infty}_{-\infty} e^{-\frac{(p^{(i)})^2}{2m_ik_{B}T}}dp^{(i)}\bigg)^{3}\bigg(\int^{\infty}_{-\infty} \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{(i)}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg)\tag{5}
\end{align*}
運動量の部分は積分できますよね。
\int^{\infty}_{-\infty} e^{-\frac{(p^{(i)})^2}{2m_i k_{B}T}}dp^{(i)}\tag{6}
\end{align*}
の部分です。
これはガウス積分の公式を使います。
ガウス積分を使うと(6)式は、
\int^{\infty}_{-\infty} e^{\frac{-(p^{(i)})^2}{2mk_{B}T}}dp^{(i)}=\sqrt{2m_i k_{B}T}\tag{7}
\end{align*}
となります。
なので、(6)式は・・・
Z = \frac{1}{(2\pi\hbar)^{3N}}\Pi_{i}^{N}\bigg(2m_{i}k_{B}T\bigg)^{\frac{3}{2}}\bigg(\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{(i)}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg)\tag{8}
\end{align*}
と、すっきりします。
まとめ
「3次元(空間)、粒子数N個」でのハミルトニアン
から、分配関数を計算しました。
Z = \frac{1}{(2\pi\hbar)^{3N}}\Pi_{i}^{N}\bigg(2m_{i}k_{B}T\bigg)^{\frac{3}{2}}\bigg(\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}\int^{\infty}_{-\infty} e^{-\frac{V(\{\boldsymbol{q^{(i)}}\})}{k_B T}}d\boldsymbol{q^{(i)}}\bigg)\tag{8}
\end{align*}
準古典近似での分配関数を求めることができました(^^♪
分配関数\(Z\)を計算することで、物理量の期待値を芋づる式に計算することができるというのが大事なポイントです(^^)/
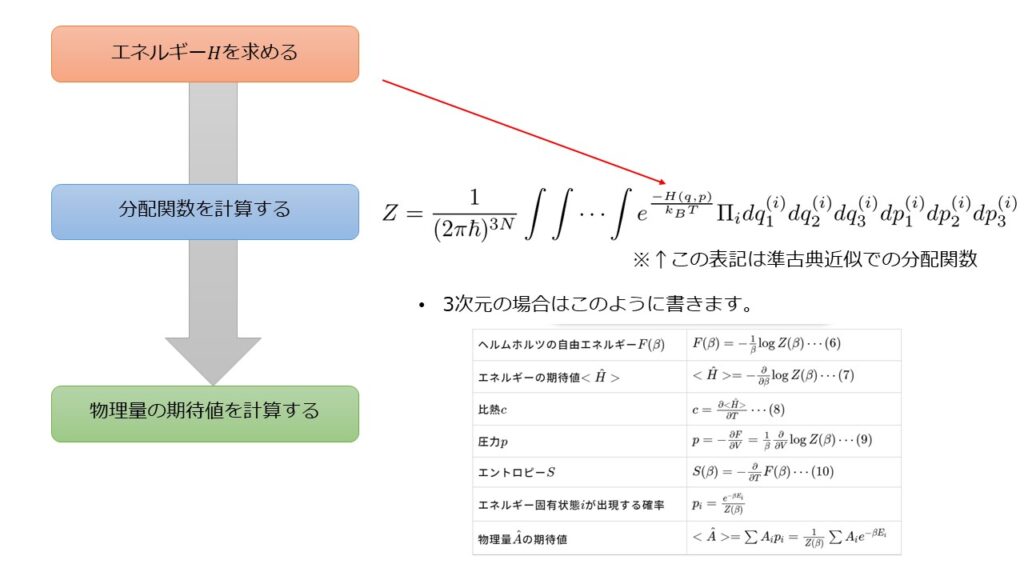

計算できる物理量の期待値の代表例がこちらです。
| ヘルムホルツの自由エネルギー\(F(\beta)\) | \(F(\beta)=-\frac{1}{\beta}\frac{\partial }{\partial \beta}\log Z(\beta)\) |
| エネルギーの期待値\(<\hat{H}>\) | \(<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)\) |
| 圧力\(p\) | \(p=\frac{1}{\beta}\frac{\partial}{\partial V}\log Z(\beta)\) |
| エントロピー\(S\) | \(S(\beta)=-\frac{\partial}{\partial T}F(\beta)=\frac{1}{\beta}\frac{\partial}{\partial T}\big(\frac{1}{\beta}\log Z(\beta)\big)\) |
| エネルギー固有状態\(i\)が出現する確率 | \(p_{i}=\frac{e^{-\beta E_{i}}}{Z(\beta)}\) |
| 物理量\(\hat{A}\)の期待値 | \(<\hat{A}>=\sum A_{i}p_{i}=\frac{1}{Z(\beta)}\sum A_{i}e^{-\beta E_{i}}\) |