こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
「比熱の温度依存性の理解のため」のための記事に記事を書いております。
比熱の温度依存性については、「統計力学の知識」が必要であります。
分配関数から物理量の期待値を芋ずる式に導出。
本記事を読むにあたって詳細の計算まで踏み込んで議論していては、時間がかかりすぎるため前提にしている知識が3つあります。
必要とする前提知識
- 古典力学
- 統計力学(平衡)
- じゃっかんの量子力学の知識
前回の記事のまとめ
前回の記事の内容を軽くおさらいしておきましょう。
【統計力学】芋づる式に物理量を作る「分配関数」とかいう便利な装置
さっそく統計力学の知識の範囲になるのですが、粒子(分子)などの粒子集団の統計的な振る舞い(物理量の期待値)を知るために、分配関数というのを使います。
「分配関数」は系の集団がもつ統計的な振る舞い(物理量)を知るための発生装置だと思っておきましょう。
ここではカノニカル分布における分配関数を考えることにしましょう。
下記の絵のように熱浴との間でのみエネルギーを自由にやりとりできる系を考え、「注目している系」では微視的な状態のエネルギー\(E_{i}\)をとる確率分布は、
と書くことができます
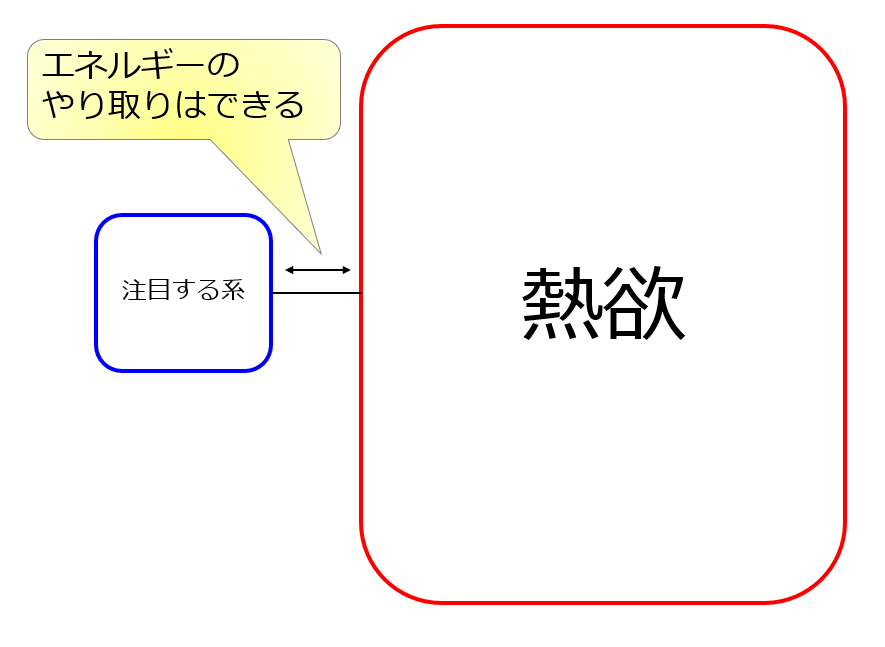

この確率分布の規格化定数になっているものが分配関数と呼ばれるものです。
※カノニカル分布と付けた理由は、統計的な集団をどのような確率モデルで考えるかによって「ミクロカノニカル分布」「カノニカル分布」「グランドカノニカル分布」という統計分布があり、本記事ではカノニカル分布のみ限った話をしているという意味を含んでいますので注意してください_(._.)_
具体的な計算をしてみましょう(^^)/
(例)調和振動子ポエンシャル系での分配関数
「調和振動子ポテンシャルに閉じ込められた1粒子のエネルギー固有値をシュレディンガー方程式から計算して、分配関数を求める。」ということをしてみます。
調和振動子ポテンシャルによるハミルトニアン
↓こう書いた方がいいかな・・・
これをシュレディンガー方程式に代入してエネルギー値を求めます。
シュレディンガー方程式(定常状態)
(2)式を(3)式に代入するとエネルギー固有値は以下のように決まります。
1粒子の調和振動子ポテンシャルによるエネルギー固有値
※\(n=0,1,2\cdots\)
調和振動子ポテンシャルに依る分配関数を求める準備ができましたので、(4)式を分配関数の(1)式に代入して分配関数を求めることができます。
シグマの和の部分を展開します。
これは無限等比数列というやつです。
高校生でも習う無限等比数列の公式を使えば、調和振動子による分配関数は簡単に求まります。
求まりました(^^)/
分配関数から種々の物理量の期待値が計算できる
分配関数の計算ができたところで、以下の種々の物理量の期待値が芋づる式に計算できます。
公式にみたいにして覚えてしまっても良いです。。。以下の式の導出は、別途「統計力学」で学ぶとして、
分配関数を計算すれば、色んな物理量が計算できるのかーっていうのを感じてもらえればと思います。
カノニカル分布での分配関数
| ヘルムホルツの自由エネルギー\(F(\beta)\) | \(F(\beta)=-\frac{1}{\beta}\log Z(\beta)\cdots (6)\) |
| エネルギーの期待値\(<\hat{H}>\) | \(<\hat{H}>=-\frac{\partial }{\partial \beta}\log Z(\beta)\cdots (7)\) |
| 比熱\(c\) | \(c=\frac{\partial <\hat{H}>}{\partial T}\cdots (8)\) |
| 圧力\(p\) | \(p=-\frac{\partial F}{\partial V}=\frac{1}{\beta}\frac{\partial}{\partial V}\log Z(\beta)\cdots (9)\) |
| エントロピー\(S\) | \(S(\beta)=-\frac{\partial}{\partial T}F(\beta)\cdots (10)\) |
| エネルギー固有状態\(i\)が出現する確率 | \(p_{i}=\frac{e^{-\beta E_{i}}}{Z(\beta)}\) |
| 物理量\(\hat{A}\)の期待値 | \(<\hat{A}>=\sum A_{i}p_{i}=\frac{1}{Z(\beta)}\sum A_{i}e^{-\beta E_{i}}\) |
分配関数を知るとこれだけの物理量が計算できるのですから、とても便利なものだなという印象を持ってもらえたかと思います。
以下に、「エネルギー固有値」から「分配関数」を計算して「物理量の期待値」を求める流れをまとめておきます。
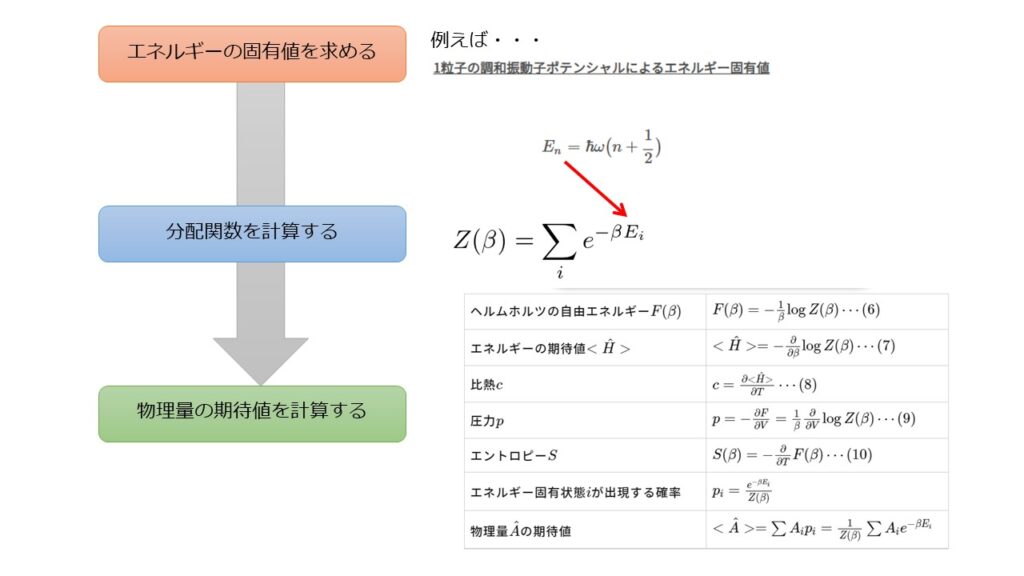

まとめ
ポイント
「分配関数」は系の集団がもつ統計的な振る舞い(物理量)を知るための発生装置だと思っておきましょう。














Fの式が違うと思われます
ご指摘ありがとうございます。
修正致します。