【理想気体の比熱の温度依存性(1)】内部エネルギーとは何か。

こんにちは（@t_kun_kamakiri）(‘◇’)ゞ

最近疑問に思っていることがあります。

比熱\(C_{V}\)
比熱比\(\gamma=\frac{C_{p}}{C_{v}}\)

の温度依存性についてです。
比熱が温度依存する理由って知っていますか？

カマキリ

僕は、理由を知りませんでした。

「比熱の温度依存性」のための記事を以下にまとめました。

まとめ

【まとめ】比熱の温度依存性について。古典論と量子論から理解する。

なぜ比熱や比熱比の温度依存性について考えようと思ったかというと、

比熱比の温度依存性について書かれている記事があまり見受けられず、実際どうなっているのかを知りたくなったからです。

※Twitterでもこういった内容で発信しています。

比熱比が温度依存性があって、温度上昇に対して比熱比は下がる。。。

とよく見かけるけどどんな理論なのか知りたい。
γ=Cp/Cvなので温度上昇すると内部にたまるエネルギーが外へする仕事よりもよりたまってくるというイメージなのかな(　・ω・)

— カマキリ🐲@ブログ書いている (@t_kun_kamakiri) 2019年10月1日

面白さ
比熱の温度依存性は古典力学の範囲で議論しても一向に理解ができないという結論になります。
実験事実として比熱は温度依存性があるのですが、「マクロな視点で見る熱力学」でも「ミクロな視点から統計的に粒子の運動を考える統計力学」でも比熱の温度依存性についての理論的な理解を得ることができなかった・・・・という歴史があるようです。
比熱の温度依存性については、量子力学の登場を待つしかなかったのですが、現在の量子力学は実験事実を示す矛盾の無いモデルとして構築されています。
比熱の温度依存性の理論的理解にもやはり量子力学が必要であるということを見ていきたいと思います。

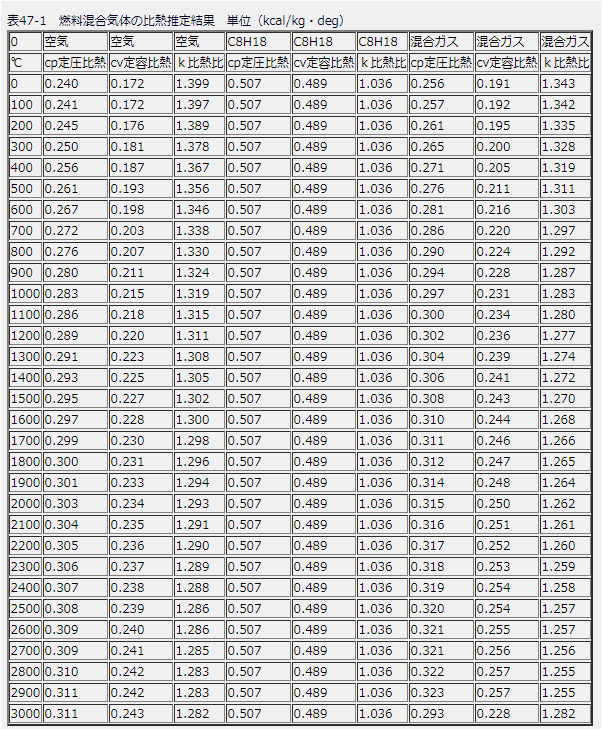
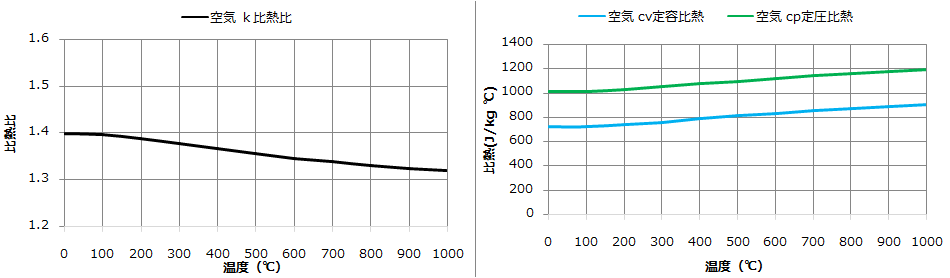
空気の比熱の温度依存性であれば下記のデータから入手できますので、比熱比の温度依存性のグラフにしてみると以下のようになります（下図左）。

空気の比熱（入手データ）

カマキリ

これは面白い！温度が上がると、比熱は上昇し比熱比は減少するのか！！

比熱（や比熱比）と言ってもおそらく理想気体に限った話だと思われます・・・

グラフから言えること

定積比熱\(C_{V}\)と定圧比熱\(C_{p}\)は温度とともに増加
比熱比\(\gamma=\frac{C_{p}}{C_{V}}\)は温度上昇に従って減少

というのが正しいのではないかと考えています。
※全種類の分子を探せばもちろん例外はあるかもしれませんが・・・

こちらは、古典力学でもマクスウェルとボルツマンが抱えていた「最大の課題」としているくらい謎めいたものでしたが、

「量子力学」と「平衡統計力学」という学問の発展によって、比熱の温度依存性については解決をしたそうです。

統計力学〈1〉 (新物理学シリーズ)

田崎晴明

3,740円(11/21 11:30時点)

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

上記の参考書を読むことで、比熱の温度依存性についての理解が深まったので、

シリーズ化して「比熱の温度依存性について」の知識を共有しておきたいと思います。

というわけで、

本記事から学べる事

「なぜ、温度が上がると比熱は上昇し、比熱比\(\gamma\)は減少するのか？」を理解するにあたって・・・

内部エネルギーとは何か？

を理解したいと思います。

エネルギー分配則についての知識も付きます(^^)/

理想気体に限った話に絞って最終的な結論を考えようと思います。

復習：定積比熱\(C_{V}\)と定圧比熱\(C_{p}\)
1. 復習：定積比熱とは？
2. 復習：定圧比熱とは？
内部エネルギーとは何か？
エネルギー等分配則は、「運動量の2乗」「位置の2乗」に比例していることが本質である
まとめ

復習：定積比熱\(C_{V}\)と定圧比熱\(C_{p}\)

定積比熱と定圧比熱が何かを話す前に、「比熱ってなんだろう(ノД`)・゜・。」となっていては辛いので不安な方は下記の記事で勉強しておきましょう(^^)/

比熱についての知識がある方は飛ばしてください。

比熱についての記事

熱容量と比熱の違いをわかりやすく解説【図解あり】

比熱と一言で言っても、定圧比熱\(C_{V}\)と定積比熱\(C_{p}\)があります。

定積比熱と定圧比熱の理解（熱力学）

定積比熱と定圧比熱の定義

上記の記事から一部を抜粋して「定積比熱と定圧比熱」の違いについて解説します。

復習：定積比熱とは？

定積比熱とは、体積が変化しない状況下において定義されます。

定積比熱

体積一定下において、単位質量当たり、1K（もしくは1℃）上昇させるのに必要な熱量(J)
単位：J/kg K

たとえばどんな状況かというと、断熱容器に囲まれた系（何か物質：例えば鉄など）の1kgを、1℃上昇させるのに必要な熱量が定積比熱です。

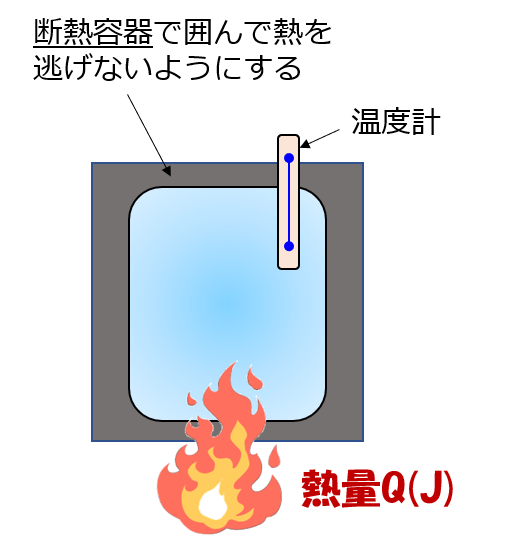
この場合は体積膨張しないので、加えられた熱量が全て内部に蓄えられるエネルギーになります。

復習：定圧比熱とは？

定圧比熱とは、圧力が変化しない状況下において定義されます。

定圧比熱
圧力一定下において、単位質量当たり、1K（もしくは1℃）上昇させるのに必要な熱量(J)
単位：J/kg K

例えば、断熱容器に囲まれている容器の赤色の敷居は自由に動くものとすると、青色の系は常に大気圧と釣り合うくらいの力でゆ～っくり敷居を右へ押していきます（準静的過程）

準静的過程（静的と思えるくらいゆっくり）

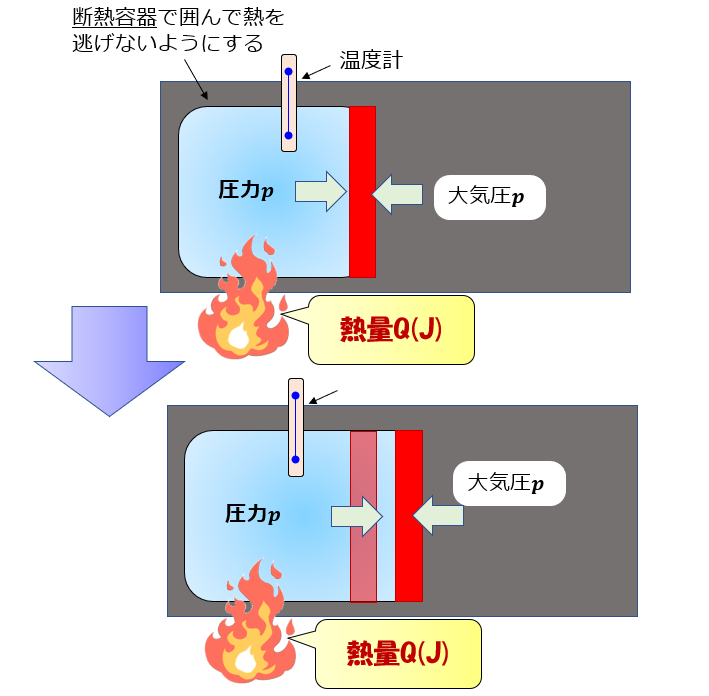
この場合は熱量が加えられても、蓄えられた内部エネルギーで一瞬大気圧より圧力が増し(\(\alpha\))、圧力が増した分で外へ仕事をし体積膨張します(\(\beta\))。
しかし、体積膨張したのでまたもとの大気圧に戻ります。

※この(\(\alpha\))と(\(\beta\))の仮定がほぼ無視できるくらいの時間スケールである場合において平衡状態の熱力学というのはとても有効的です。

これを繰り返して、じわじわと膨張するような圧力が一定の状況下において単位質量当たり、1K（もしくは1℃）上昇させるのに必要な熱量(J)が定圧比熱になります。

定圧比熱は、膨張させるのに余分にエネルギーを使っているため、体積が膨張しない場合(定積)と比べて温度1K上昇させるのに余分にエネルギーが必要になります。

ゆえに、通常の気体においては定圧比熱\(c_p\)は定積比熱\(c_V\)より大きな値になります。

\begin{align*}c_{p}\geq c_{V}\tag{2}\end{align*}

まとめると、
比熱とは「とある条件下（体積一定、圧力一定）で、1kgの物質の温度を1K上昇させるのに必要なエネルギー」という意味です。

内部エネルギーとは何か？

カマキリ

ここから内部エネルギーの話をします。

比熱の説明のところで、「1kgの物質の温度を1K上昇させるのに必要なエネルギー」と言いましたが、どういったエネルギーを意味しているのかを考えたいと思います。

比熱の温度依存性を知るために、この「1kgの物質の温度を1K上昇させるのに必要なエネルギー」の「エネルギー」の正体をミクロな視点で考えなおすことがとても大事になります。

そのエネルギー保存則を、「熱量」「気体(系)がもつ内部エネルギー」「力学的な仕事量」の3つに分解したものを等式にしたものが熱力学第一法則です。

熱力学第一法則：熱量=内部エネルギー+気体(系)がする仕事量

下記のように、「加えた熱量」によって、「気体(系)が外に仕事」を行い、余った分が「内部のエネルギーに蓄えられる」と解釈します。

それを式で表すと、

熱量=内部エネルギー+気体(系)がする仕事量・・・(1)

ということになります。

カマキリ

式じゃないけど

この、内部エネルギーってなんのか？
この内部エネルギーこそが「1kgの物質の温度を1K上昇させるのに必要なエネルギー」の「エネルギー」の正体ということです。
内部エネルギーをミクロな視点で詳細に考えることが比熱や比熱比の温度依存性を解くカギになるです！！

内部エネルギーとは「気体の運動エネルギー」「気体分子間の相互作用」「位置エネルギー」

熱力学はマクロな視点での学問であるため、内部エネルギーから「温度や圧力」を知ればそれで十分なのですが、比熱の温度依存性を考えるにあたっては内部エネルギーについてミクロな視点から考える必要があります。

ちなみに、

内部エネルギーとは系が全体として持っている「運動エネルギー、相互作用エネルギー、位置エネルギー」などを指しています。

入ってきた熱量\(Q\)（正確には正味の熱量なので、出ていっている熱量も含みます）
外へする仕事\(W\)
その他の全てのエネルギーを内部エネルギー\(U\)

としています。

※外気との温度差によって熱の放出を「熱量\(Q\)の逃げとして、正味の熱量」と考えるか「内部エネルギーの減少」と考えるかは難しいですが、今は外気との温度差による熱の逃げが無いものとします。

冒頭で話したように、今回は理想気体を考えているので、この内部エネルギーは「気体の運動エネルギー」（2原子原子以上であれば「原子間相互作用」も含む）だけに依ると考えることとします。（分子間の相互作用は考えないよ・・・ということです）

カマキリ

運動エネルギーと言っても、注意が必要である！！

気体の運動に関係する運動エネルギーの種類

並進運動のエネルギー
回転運動のエネルギー
振動のエネルギー

など・・・複数あることに注意する必要があります。

これらが、ミクロな視点で内部エネルギーの正体であると考えることになります。

熱力学は分子の種類などのミクロな視点での学問ではないため、気体分子の１つ１つの運動の詳細には興味が無いために「内部エネルギー」と一括りにしてしまっていますが、

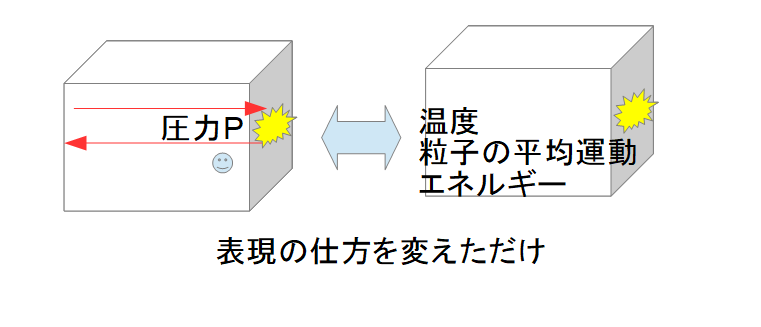
気体分子運動論（あくまで理想気体）は、熱力学と対応する量を力学的な視点から個々の分子の運動の平均値として考え直すことで熱力学での「圧力、温度」というものを再認識しています。

気体分子運動論

ここで少し気体分子運動論の話をすると、個々の分子の運動エネルギーの平均化したもの\(\frac{1}{2}m\bar{v}^2=\frac{1}{2}k_{B}T\)となることが導かれます。

ボルツマン定数：\(k_{B}\)
温度：\(T\)

※\(\bar{v}\)とすると平均を意味していますが、ここからは自明としてバーをとった\(v\)で表現することとします。

ここで大事なのが、

1自由度で\(\frac{1}{2}k_{B}T\)のエネルギー

を有しているということです。

単原子分子なら「並進運動エネルギー」のみ

単原子分子なら並進運動のエネルギーのみです。

並進運動エネルギー

1自由度（\(x\)方向のみ)なら運動エネルギー：\(\frac{1}{2}mv_x^2\)→\(\frac{1}{2}k_{B}T\)
2自由度（\(x,y\)方向のみ)なら運動エネルギー：\(\frac{1}{2}m(v_x^2+v_y^2)\)→\(\frac{2}{2}k_{B}T\)
3自由度（\(x,y,z\)方向)なら運動エネルギー：\(\frac{1}{2}m(v_x^2+v_y^2+v_z^2)\)→\(\frac{3}{2}k_{B}T\)

ということです。

2原子分子なら「回転運動エネルギー」＋「振動運動エネルギー」

2原子分子の場合は、「回転の運動エネルギー」と2原子が距離を離れたときに感じる「振動運動エネルギー」の2つがあります。

2原子分子の場合の自由度については、

2原子がそれぞれ位置を変える（\(x,y,z\)の3自由度）ことによる運動エネルギー（合計6自由度）と、
2原子の相対位置によって生じる2原子間の振動によるエネルギー（1自由度）

の合計7自由度あります。

エネルギーの記述を簡単にするために、

2原子の重心の運動（重心運動）
2原子の重心に対する運動（相対運動）

の2つにわけて考えることにします。

結局は自由動は7自由度です。

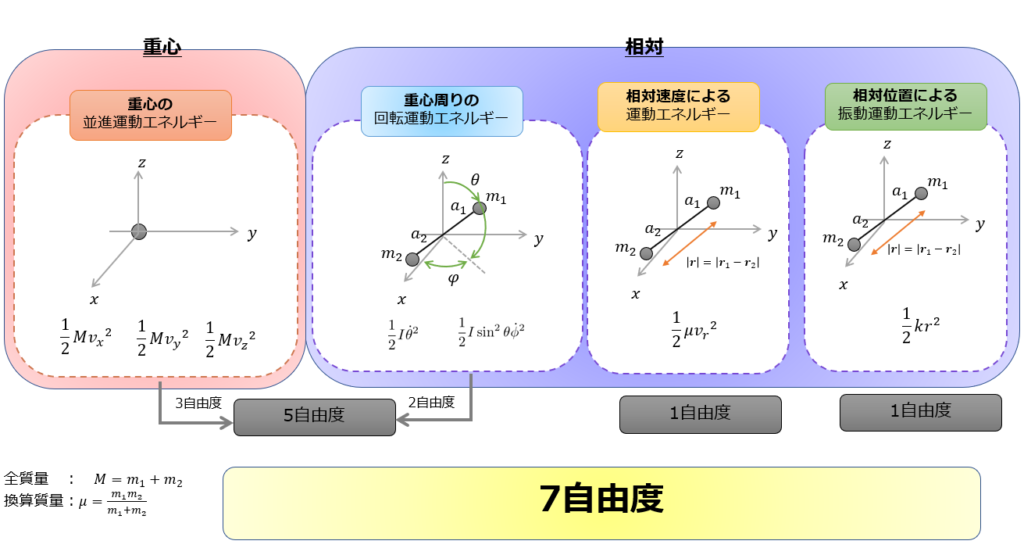
以上をまとめます↓。

並進運動のエネルギーと回転運動のエネルギーと振動運動のエネルギーを含めると以下となります。

重心：並進運動エネルギー

1自由度（\(x\)方向のみ)なら運動エネルギー：\(\frac{1}{2}mv_x^2\)→\(\frac{1}{2}k_{B}T\)
2自由度（\(x,y\)方向のみ)なら運動エネルギー：\(\frac{1}{2}m(v_x^2+v_y^2)\)→\(\frac{2}{2}k_{B}T\)
3自由度（\(x,y,z\)方向)なら運動エネルギー：\(\frac{1}{2}m(v_x^2+v_y^2+v_z^2)\)→\(\frac{3}{2}k_{B}T\)

相対：回転運動エネルギー

5自由度：並進運動のエネルギーと回転運動エネルギー：\(\frac{1}{2}m(v_x^2+v_y^2+v_z^2)+\frac{1}{2}I(\dot{\theta}^2+\sin^2\theta\dot{\phi}^2)\)→\(\frac{5}{2}k_{B}T\)

\(K=\frac{1}{2}I(\dot{\theta}^2+\sin^2\theta\dot{\phi}^2)\)

※慣性モーメント\(I=m_{1}a_{1}^2+m_{2}a_{2}^2\)

相対：相対距離を変えることによるエネルギー

1自由度（\(r\)方向のみ)の運動エネルギー：\(\frac{1}{2}mv_r^2\)→\(\frac{1}{2}k_{B}T\)
1自由度（\(r\)方向のみ)の振動運動エネルギー：\(\frac{1}{2}k(|\boldsymbol{r_{1}}-\boldsymbol{r_{2}}|)^2\)→\(\frac{1}{2}k_{B}T\)

つまり、自由度が\(f\)であれば、内部エネルギーに起因する分子集団の運動エネルギーは

\begin{align*}\frac{f}{2}k_{B}T\tag{2}\end{align*}

ということになります。

これがエネルギー等分配則です。

各自由度にエネルギーが\(\frac{1}{2}k_{B}T\)だけ均等に分配されたということです。

エネルギー等分配則は、「運動量の2乗」「位置の2乗」に比例していることが本質である

先ほどの運動エネルギーを運動量で表示してみます。

\(x,y,z\)方向の並進運動エネルギー：\(\frac{1}{2m}(p_x^2+p_y^2+p_z^2)\)
\(\phi,\theta\)方向の回転運動エネルギー:\(\frac{1}{2I}\bigg(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2\theta}\bigg)\)

詳細は下記の参考書に譲りますが、

統計力学 (岩波基礎物理シリーズ 7)

長岡洋介

Amazon 楽天市場 Yahoo

Amazonの情報を掲載しています

結論・・・

エネルギー等分配則は、運動エネルギーが運動量の2次関数であり、自由度\(f\)とすれば、

\begin{align*}K=\sum_{i=1}^{f}\alpha_{i}^2p_{i}^2\tag{2}\end{align*}

と表されるというものから来ています。

「1自由度\(\frac{1}{2}k_{B}T\)のエネルギーに分配されるんだよ（エネルギー等分配則）」と言われているのは、運動エネルギーが運動量の2次関数だったからです。

さらに、これはエネルギーが運動量の2次関数というだけにはとどまらず、エネルギーが位置\(x\)の2次関数であっても、エネルギー分配則が成り立ちます。

エネルギー等分配則は、
位置によるエネルギーが位置の2次関数であり、自由度\(f\)とすれば、

\begin{align*}K=\sum_{i=1}^{f}\alpha_{i}^2p_{i}^2\tag{2}\end{align*}

と表されるというものから来ています。

自由度としてひとつカウントしてポテンシャルエネルギーからも\(\frac{1}{2}k_{B}T\)が生じているということになります。

だから分子の感じるポテンシャルエネルギーが\(\frac{1}{2}m\omega^2x^2\)のような形をしていても、\(\frac{1}{2}k_{B}T\)が生じているということになります。

エネルギー分配則のポイント

\(K=\sum_{i}^{f}\alpha_{i}p_{i}^{2}\)：エネルギー=\(\frac{f}{2}k_B T\)
\(U=\sum_{i}^{f}\beta_{i}x_{i}^{2}\)：エネルギー=\(\frac{f}{2}k_B T\)

もし仮に、同じ固有振動数\(\omega\)をもつ\(N\)個の振動子系のハミルトニアン\(H\)を考えると、

\begin{align*}H=\sum_{i=1}^{N}\bigg(\frac{p_{i}^2}{2m}+\frac{1}{2}m\omega^2x_{i}^2\bigg)\tag{3}\end{align*}

となり、内部に蓄えられるエネルギーは、

\begin{align*}E=\frac{1}{2}NkT\times 2\tag{4}\end{align*}

となります。

これは、エネルギーが「運動エネルギーの自由度」と「調和振動子エネルギーの自由度」に\(\frac{k_B T}{2}\)ずつ等分配されていることを示しています。

繰り返しになりますが、このようなエネルギー分配則は運動エネルギーも調和振動子エネルギーも「運動量\(p\)の2次関数」か「位置\(x\)の2次関数」になっていることに起因しているということを覚えておきましょう(^^)/

まとめ

内部エネルギーとは系が全体として持っている
「運動エネルギー、相互作用エネルギー、位置エネルギー」
などを指しています。
気体の運動に関係する運動エネルギーの種類

並進運動のエネルギー
回転運動のエネルギー
振動のエネルギー
単原子分子は、並進運動エネルギーだけ
2原子分子は、並進運動エネルギー、回転の運動エネルギー、振動運動エネルギー

エネルギー等分配則により、1自由度\(\frac{1}{2}k_{B}T\)にエネルギーが分配されています。
↑これは、運動エネルギーも調和振動子エネルギーも「運動量\(p\)の2次関数」か「位置\(x\)の2次関数」になっていることに起因しています。

まとめると・・・・

内部エネルギー

	重心の並進運動エネルギー	重心まわりの回転運動エネルギー	相対位置変化による運動エネルギー	振動運動エネルギー	全エネルギー
単原子分子	\(\frac{1}{2}k_{B}T\times 3\) \(x,y,z\)：3自由度	–	–	–	\(\frac{3}{2}k_{B}T\)
2原子分子	\(\frac{1}{2}k_{B}T\times 3\) \(x,y,z\)：3自由度	\(\frac{1}{2}k_{B}T\times 2\) \(\phi,\theta\)：2自由度	\(\frac{1}{2}k_{B}T\times 1\) \(x,y,z\)：1自由度	\(\frac{1}{2}k_{B}T\) 1自由度	\(\frac{7}{2}k_{B}T\)

カマキリ

内部エネルギーの表式がわかったところで・・・

比熱は内部エネルギーの温度微分であるので(上記の内部エネルギーの表から温度\(T\)を取るだけ)、

比熱

	重心の並進運動エネルギー	重心まわりの回転運動エネルギー	相対位置変化による運動エネルギー	振動運動エネルギー	全エネルギー
単原子分子	\(\frac{1}{2}k_{B}\times 3\) \(x,y,z\)：3自由度	–	–	–	\(\frac{3}{2}k_{B}\)
2原子分子	\(\frac{1}{2}k_{B}\times 3\) \(x,y,z\)：3自由度	\(\frac{1}{2}k_{B}\times 2\) \(\phi,\theta\)：2自由度	\(\frac{1}{2}k_{B}\times 1\) \(x,y,z\)：1自由度	\(\frac{1}{2}k_{B}\) 1自由度	\(\frac{7}{2}k_{B}\)