ポアッソン括弧式を用いた正準変換であるための必要十分条件

『計算過程はどうでも良い。

結果だけ知ってさえいれば十分である。

しかし、計算過程を手を動かして進めることで、「何が出発点」で「何の結果」を得たのか・・・・

そしてその結果のための「条件は何か」を深く知ることになるでしょう。』

by　宇宙に入ったカマキリ

ポアッソン括弧式を勉強してそう思ったんです(笑)

簡単な表式に書くことができてそれを見やすく、覚えやすい形に書き下すことに意味があるのではないかと思っています。

さて、前回は下記のようにポアッソン括弧式を用いた関係式を示しました。

\begin{align*}\{q_{i},q_{j}\}_{q,p}=0\end{align*}

\begin{align*}\{p_{i},p_{j}\}_{q,p}=0\end{align*}

\begin{align*}\{q_{i},p_{j}\}_{q,p}=\delta {ij}\end{align*}

↑これですね。

本記事

変数\(\{q_{i}\},\{p_{i}\}\)から、それらを変数とした別の変数\(\{Q_{i}\},\{P_{i}\}\)（正確には\(\{Q_{i}(\{q_{i}\},\{p_{i}\})\},\{P_{i}\}(\{q_{i}\},\{p_{i}\})\)）のように正準変換した際も、

\begin{align*}\{Q_{i},Q_{j}\}_{q,p}=0\end{align*}

\begin{align*}\{P_{i},P_{j}\}_{q,p}=0\end{align*}

\begin{align*}\{Q_{i},P_{j}\}_{q,p}=\delta {ij}\end{align*}

という関係は同じ。

↑これを示そうと思います。

これにはとても大事な関係式を使います。
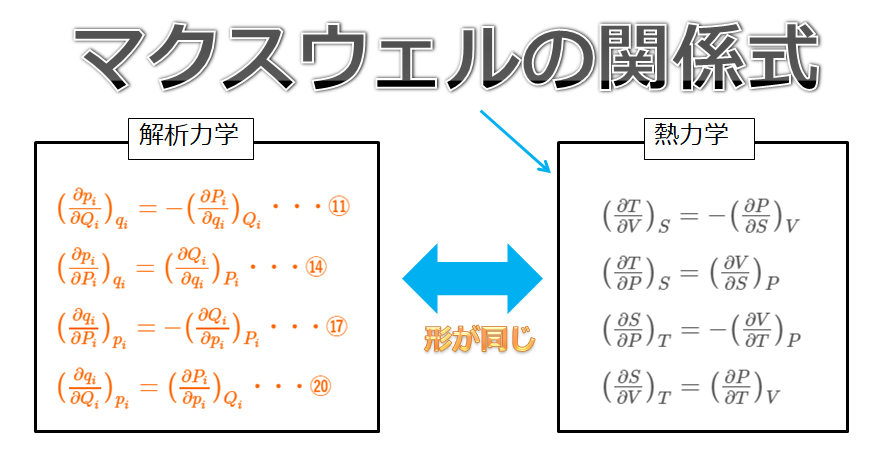
↓こちらに下記のような関係式を導きました。

まさかこんなところでこの①～④式の関係式を使うことになるとは思ってもいませんでした(笑)

\begin{align*}\big(\frac{\partial p_{i}}{\partial Q_{i}}\big)_{q_{i}}=-\big(\frac{\partial P_{i}}{\partial q_{i}}\big)_{Q_{i}}\cdot\cdot\cdot (1)\end{align*}

\begin{align*}\big(\frac{\partial p_{i}}{\partial P_{i}}\big)_{q_{i}}=\big(\frac{\partial Q_{i}}{\partial q_{i}}\big)_{P_{i}}\cdot\cdot\cdot (2)\end{align*}

\begin{align*}\big(\frac{\partial q_{i}}{\partial P_{i}}\big)_{p_{i}}=-\big(\frac{\partial Q_{i}}{\partial p_{i}}\big)_{P_{i}}\cdot\cdot\cdot (3)\end{align*}

\begin{align*}\big(\frac{\partial q_{i}}{\partial Q_{i}}\big)_{p_{i}}=\big(\frac{\partial P_{i}}{\partial p_{i}}\big)_{Q_{i}}\cdot\cdot\cdot (4)\end{align*}

それと、

ポアッソン括弧式
\(\{q_{i}\},\{p_{i}\}\)を変数とする、関数\(f(\{q_{i}\},\{p_{i}\})\)と\(g(\{q_{i}\},\{p_{i}\})\)に対して、

\begin{align*}\{f,g\}_{q,p}=\sum_{k}\big( \frac{\partial f}{\partial q_{k}}\frac{\partial g}{\partial p_{k}}-\frac{\partial f}{\partial p_{k}}\frac{\partial g}{\partial q_{k}}\big)\cdot\cdot\cdot (5)\end{align*}

これを引っさげて証明していきましょう。

\(\{Q_{i},Q_{j}\}_{q,p}=0\)について

\begin{align*}\{f,g\}_{q,p}=\sum_{k}\big( \frac{\partial f}{\partial q_{k}}\frac{\partial g}{\partial p_{k}}-\frac{\partial f}{\partial p_{k}}\frac{\partial g}{\partial q_{k}}\big)\cdot\cdot\cdot (5)\end{align*}

を単純に、

\(f\)→\(Q_{i}\)
\(g\)→\(Q_{j}\)
と置きなおします。

すると(5)式は、

\begin{align*}\{Q_{i},Q_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial Q_{i}}{\partial q_{k}}\frac{\partial Q{j}}{\partial p_{k}}-\frac{\partial Q_{i}}{\partial p_{k}}\frac{\partial Q_{j}}{\partial q_{k}}\big)\cdot\cdot\cdot (6)\end{align*}

ここで、
第一項に(3)式を・・・
第二項に(2)式を・・・・
それぞれ用いると、

(6)式は、

\begin{align*}\{Q_{i},Q_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial Q_{i}}{\partial q_{k}}\frac{\partial p_{j}}{\partial P_{k}}+\frac{\partial Q_{i}}{\partial p_{k}}\frac{\partial p_{j}}{\partial P_{k}})=-\frac{\partial Q_{i}}{\partial P_{j}}\cdot\cdot\cdot (7)\end{align*}

となります。

これは？
・・・
\(\{Q_{i}\},\{P_{i}\}\)が互いに独立な変数なので0ですね。

ゆえに、

\begin{align*}\{Q_{i},Q_{j}\}_{q,p}=0\cdot\cdot\cdot (8)\end{align*}

\(\{P_{i},P_{j}\}_{q,p}=0\)について

\(Q\)と言う文字を\(P\)に置き換えて、「はい、終了(^^♪」でも良いですが、丁寧にやりましょう(笑)

(8)式を導いた方法と全く同じ手順を踏みます。

を単純に、

\(f\)→\(P_{i}\)
\(g\)→\(P_{j}\)
と置きなおします。

すると(5)式は、

\begin{align*}\{P_{i},P_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial P_{i}}{\partial q_{k}}\frac{\partial P_{j}}{\partial p_{k}}-\frac{\partial P_{i}}{\partial p_{k}}\frac{\partial P_{j}}{\partial q_{k}}\big)\cdot\cdot\cdot (9)\end{align*}

ここで、
第一項に(4)式を・・・
第二項に(1)式を・・・・
それぞれ用いると、

(9)式は、

\begin{align*}\{P_{i},P_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial P_{i}}{\partial q_{k}}\frac{\partial q_{j}}{\partial Q_{k}}+\frac{\partial P_{i}}{\partial p_{k}}\frac{\partial p_{i}}{\partial Q_{i}})=\frac{\partial P_{i}}{\partial Q_{j}}\cdot\cdot\cdot (10)\end{align*}

となります。

これは？
・・・
\(\{P_{i}\},\{Q_{i}\}\)が互いに独立な変数なので0ですね。

ゆえに、

\begin{align*}\{P{i},P_{j}\}_{q,p}=0\cdot\cdot\cdot (11)\end{align*}

やっぱり、\(Q\)と言う文字を\(P\)に置き換えて、「はい、終了(^^♪」でも良かったかもしれません(笑)

\(\{Q_{i},P_{j}\}_{q,p}=\delta {ij}\)について

(8)(11)式と少し違いますが、それほど難しくはないでしょう(^^)/

を単純に、
\(f\)→\(Q_{i}\)
\(g\)→\(P_{j}\)
と置きなおします。

すると(5)式は、

\begin{align*}\{Q_{i},P_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial Q_{i}}{\partial q_{k}}\frac{\partial P_{j}}{\partial p_{k}}-\frac{\partial Q_{i}}{\partial p_{k}}\frac{\partial P_{j}}{\partial q_{k}}\big)\cdot\cdot\cdot (12)\end{align*}

ここで、
第一項に(4)式を・・・
第二項に(1)式を・・・・
それぞれ用いると、

(12)式は、

\begin{align*}\{Q_{i},P_{j}\}_{q,p}=\sum_{k}\big( \frac{\partial Q_{i}}{\partial q_{k}}\frac{\partial q_{j}}{\partial Q_{k}}+\frac{\partial Q_{i}}{\partial p_{k}}\frac{\partial p_{j}}{\partial Q_{k}})=\frac{\partial Q_{i}}{\partial Q_{j}}\cdot\cdot\cdot (13)\end{align*}

となります。

これは？
・・・

\(i=j\)なら1で、\(i\neq j\)なら0ですので、クロネッカーデルタ\(\delta_{ij} \)と書けます。

ゆえに、

\begin{align*}\{Q_{i},P_{j}\}_{q,p}=\delta_{ij}\cdot\cdot\cdot (14)\end{align*}

まとめ

変数\(\{q_{i}\},\{p_{i}\}\)から、それらを変数とした別の変数\(\{Q_{i}\},\{P_{i}\}\)（正確には\(\{Q_{i}(\{q_{i}\},\{p_{i}\})\},\{P_{i}\}(\{q_{i}\},\{p_{i}\})\)）のように正準変換した際も、

\begin{align*}[Q_{i},Q_{j}]_{q,p}=0\cdot\cdot\cdot (8)\end{align*}

\begin{align*}[P_{i},P_{j}]_{q,p}=0\cdot\cdot\cdot (11)\end{align*}

\begin{align*}[Q_{i},P_{j}]_{q,p}=\delta {ij}\cdot\cdot\cdot (14)\end{align*}

と書けることを示しました。

大事なのは、正準変換する前の、

\begin{align*}[q_{i},q_{j}]_{q,p}=0\end{align*}

\begin{align*}[p_{i},p_{j}]_{q,p}=0\end{align*}

\begin{align*}[q_{i},p_{j}]_{q,p}=\delta {ij}\end{align*}

と同じ関係式ではないか！！！

と、いうのもありますが、(8)(11)(14)式を導出する際に、(1)(2)(3)(4)式を使いました。

ちなみに(1)(2)(3)(4)式を導出する際に、母関数というのを使って示したのですが、

母関数は元の変数\(\{q_{i}\},\{p_{i}\}\)から、

ハミルトンの正準方程式の形を満たすように、

それらを変数とした別の変数\(\{Q_{i}\},\{P_{i}\}\)に変換するときの橋渡しのような役割をしてくれていたので、

(1)(2)(3)(4)式を使っているということは正準変換であることを含んでいるのですよね。

なので・・・

(8)(11)(14)式が成り立つということは正準変換を意味しているのです。

↑とっても重要！！

ちなみに、あまり詳細には触れませんが、変数\(\{q_{i}\},\{p_{i}\}\)から、それらを変数とした別の変数\(\{Q_{i}\},\{P_{i}\}\)（正確には\(\{Q_{i}(\{q_{i}\},\{p_{i}\})\},\{P_{i}\}(\{q_{i}\},\{p_{i}\})\)）が正準変換であるための必要十分条件は、

\begin{align*}[Q_{i},Q_{j}]_{q,p}=0\cdot\cdot\cdot (8)\end{align*}

\begin{align*}[P_{i},P_{j}]_{q,p}=0\cdot\cdot\cdot (11)\end{align*}

\begin{align*}[Q_{i},P_{j}]_{q,p}=\delta {ij}\cdot\cdot\cdot (14)\end{align*}

です。

つまり、(8)(11)(14)式であることは、逆に正準変換であると言えるのですね。

（証明は省きます）

本記事は、上記の必要十分条件の十分条件だけ示したことになりますね(^^)/