そろそろ受験本番の日が近づいてきましたね。
まずはセンター試験、それから私立試験、そして国公立の2次試験(前期・中期・後期)と忙しくとても緊張感のある日々が近づいてきます( `ー´)ノ
頑張ってほしい!!
そこで、僕もなんか受験シーズンを思い出して、試験問題を解いてみました。
2018年の京都大学の物理の問題を解いた感想
難関国立でしょう。


京都大学の物理の問題形式
こちらの問題集を見ると京都大学は基本的に穴埋め問題です。
そして、大学生の知識を問う問題が出題されます。
でも、高校生でも解くことができるように、しっかりと誘導問題になっているので、物理の本質を分かっている人はめちゃくちゃ解きやすいと思います。
- 第問が3問
- 試験時間90分
時間配分は第問1つで30分(穴埋め形式)です。
7割~8割くらいにして得点源にしたい科目ですね!(^^)!
2018年の京都大学の問題と解答の入手先
では、問題を以下から入手しましょう。
※代ゼミからダウンロードしました。
では、本題に移りましょう。
各第問の分野
- 第1問:力学(空気抵抗による問題)
- 第2問:電磁気学(電場と磁場による電子の運動の問題)
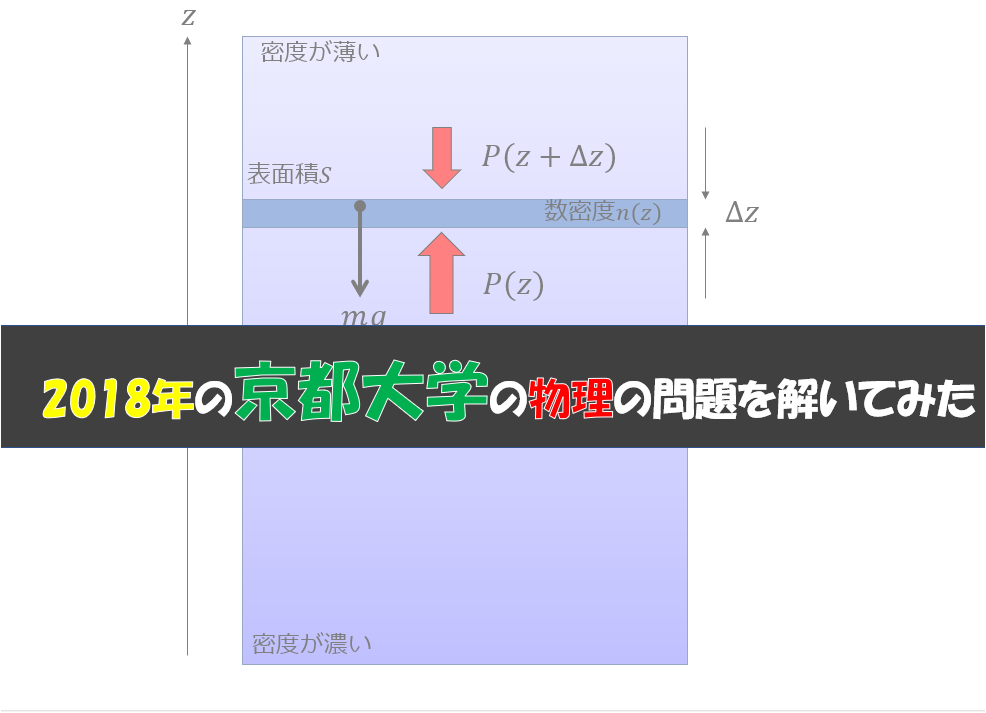
- 第3問:熱力学(重力がかかっている気体の圧力などを求める問題)
各第問に3問くらいに分かれた構成で、3問目以外は解答したいところですかね。
なので、高校生なら7割~8割くらいは取れそうな問題です。
問題自体は穴埋め式で、高校生が習わないところは誘導問題にしていたので、良問な気がしましたけど、穴埋め問題じゃなかったら大学の問題じゃないか!!って思いました。
第1問:力学の問題
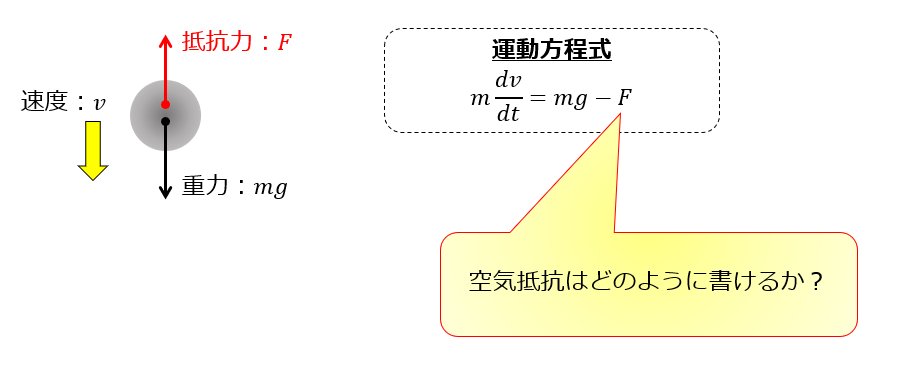

こちらは、物体が空気抵抗によって力を受け、終端速度がどうなるかという問題です。
解いた感想・・・
って感じです。
ただ、微分方程式を知らない高校生が解くという立場に立つと、「ビクっ」ってすると思います。
しかし、京都大学はそこを高校生が知らなくても解けるように誘導問題にしてくれています。
ってことで、修士卒の僕は大学で学んだ知識をフルに活かして解いてやりました。
そんなことより気になったのが以下の点です!!
実現象は空気抵抗、すなわち流体における抵抗は、
流体における抵抗について・・・
- 速度に比例するのか?
- 速度の2乗に比例するのか?
これが気になりました。
ですので・・・
Twitterでアンケートを取ってみました(‘ω’)
結果は以下の通りです。
2018年の京都大学の物理の問題
・「抵抗が速度に比例する」
・「抵抗が速度の2乗に比例する」
というお話がありました。例えば球体のまわりの流れを考える場合とかを想像します。https://t.co/3jee07bc8X
— 宇宙に入ったカマキリ@物理ブログ (@t_kun_kamakiri) 2019年1月14日
「抵抗力なんて流れによって変わるだろ」って思われている方が大半ですね(‘ω’)
そうなんです。
抵抗力は流れによって変わるんです。
こちらについては解説を加えました!(^^)!
第2問:電磁気学
第2問は電磁気学の問題です。
こちらは高校生にとってはとても解きやすい問題だったでしょう。
問題を解くための方針
- 力を分解する
- 運動方程式を立てる(運動方程式が解けなければエネルギーの保存則を使う)
- 初期条件を与える
基本的にはこれで問題は解けるだろうと思いました。
※重力、地磁気などは考慮しない
(1)電場のみの問題
電子の質量:\(m\)
電子の電荷:\(-e\)
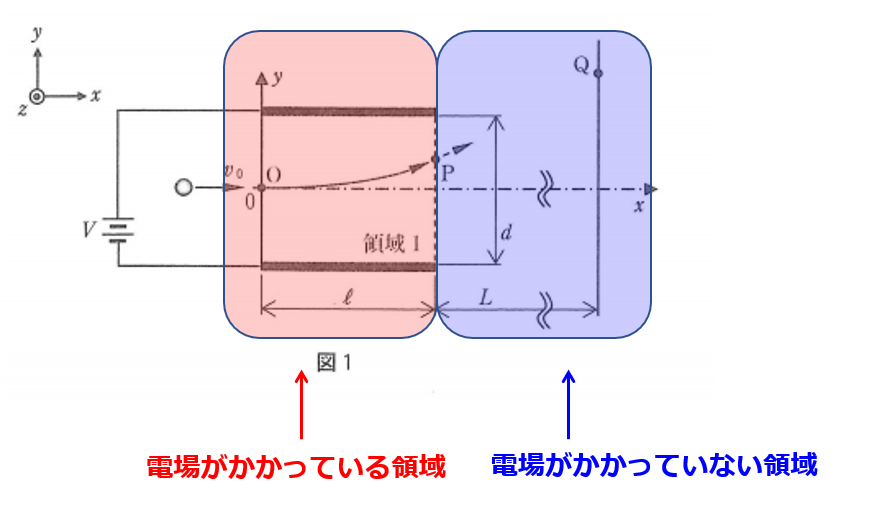

こんな感じの問題です。
電場がかかっている領域と電場がかかっていない領域があります。
こういった状況で「ある時刻には電子はどの位置にいるでしょう?」といった問題です。
これは各領域で力が異なる(つまり運動方程式が変わる)ということに注意するだけですね。
まず、領域1(赤色)で\(x\)方向と\(y\)方向で力を分解します。
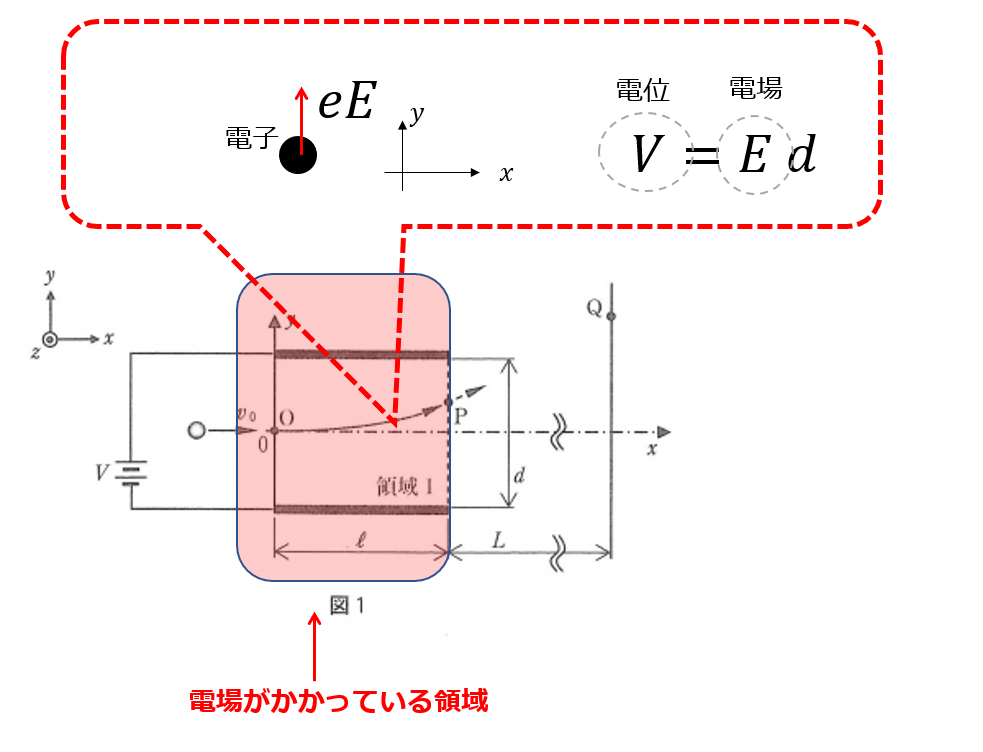

次に、運動方程式を立てます。
\(x\)方向:\(m\frac{dv_{x}}{dt}=eE\)
\(y\)方向:\(m\frac{dv_{y}}{dt}=0\)
※今回は電場\(E\)ではなく、電位\(V\)が与えられていたので注意が必要です。
電場\(E\):単位電荷あたりにかかる力
電位\(V\):単位電荷がもつ静電ポテンシャル
要するに電位は、重力でいうところの位置エネルギーみたいなものですかね。
だから、\(V=Ed\)という関係が成り立つということに注意しながら問題を解きます( `ー´)ノ
初期条件も確認しておきましょう。
位置:\((x,y)=(0,0)\)
速度:\((v_{x},v_{y})=(v_{0},0)\)
これは、サクッと解くだけですね。
まず、青色\(x\)方向と\(y\)方向で力を分解します。
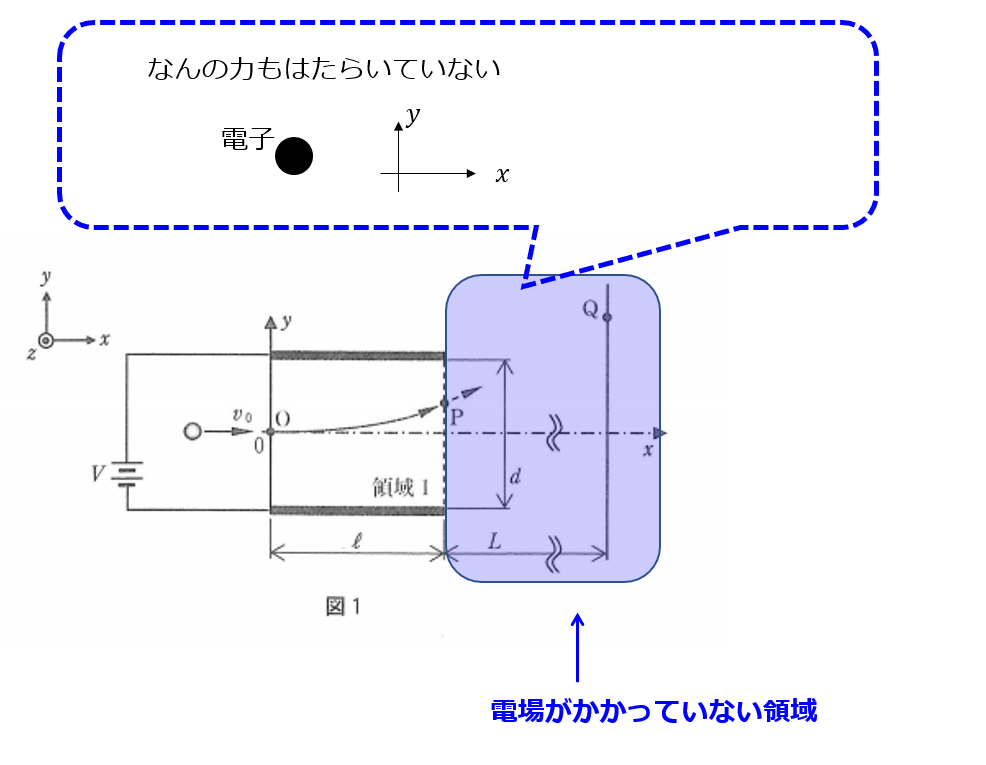

次に、運動方程式を立てます。
\(x\)方向:\(m\frac{dv_{x}}{dt}=0\)
\(y\)方向:\(m\frac{dv_{y}}{dt}=0\)
今度は電場がない領域ですので、電子が受けている力は何もありません。
初期条件も確認しておきましょう。
位置:\((x,y)=(l,領域1で決まる)\)
速度:\((v_{x},v_{y})=(v_{0},領域1で決まる)\)
初期条件だけ、領域1の問題を解いてから決められるということです。
ここまでもサクサクっといけるでしょう!!
(2)磁場がある場合
電子の質量:\(m\)
電子の電荷:\(-e\)
電場\(E\)が\(y\)方向に、磁束密度\(B\)が\(-z\)方向にかかっている状況です。
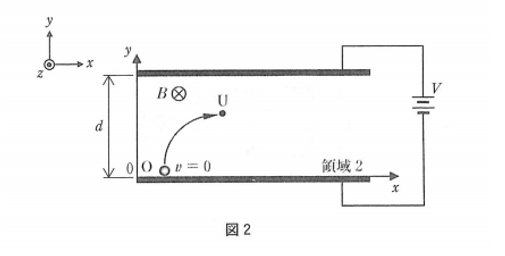

磁場によって生み出される力というのを、5年以上使っていないので忘れました(*_*;
磁場によって生み出される力とは、「ローレンツ力」ということでしょう。
かろうじて外積であることを覚えています
※電荷\(q\)。今の問題設定では\(q=-e\)
僕はこんな感じで、ローレンツ力の向きを決めています(右手を使います)
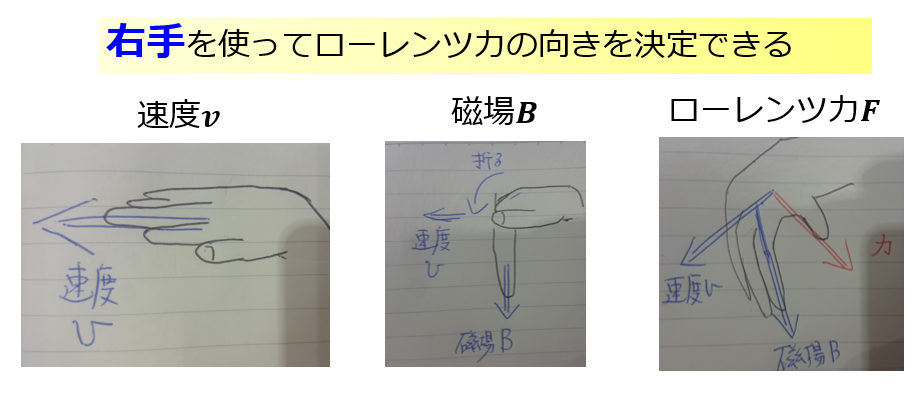

ちなみに、皆さんはローレンツ力の向きをどのように決めているのかをTwitterでアンケートを取りました。
高校生のとき、電磁力(ローレンツ力)の向きをどうやって決めていましたかね。
— 宇宙に入ったカマキリ@物理ブログ (@t_kun_kamakiri) 2019年1月19日
\(x\)方向と\(y\)方向で力を分解します。
電荷にマイナス符号がついていると、ややこしいので一旦\(q>0\)で方程式を立ててみます。
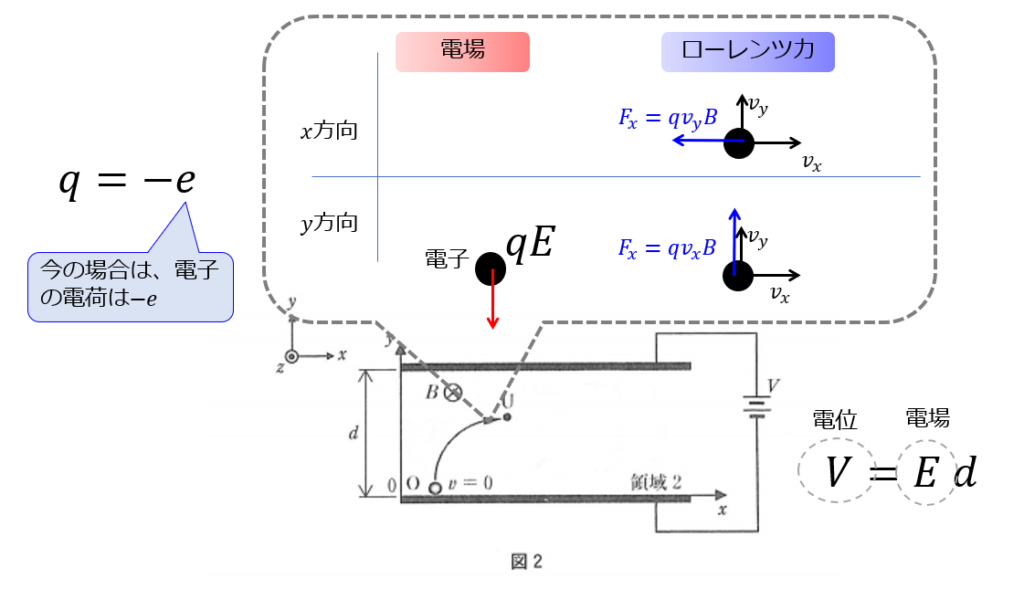

では、運動方程式を立てます。
一旦\(q>0\)で方程式を立てる。
\(x\)方向:\(m\frac{dv_{x}}{dt}=-qv_{y}B\)
\(y\)方向:\(m\frac{dv_{y}}{dt}=-qE+qv_{x}B\)
↓
↓\(q=-e\)なので、
\(x\)方向:\(m\frac{dv_{x}}{dt}=ev_{y}B\)
\(y\)方向:\(m\frac{dv_{y}}{dt}=eE-ev_{x}B\)
これを解けば良いということです。
これは高校生で解くことはまずないでしょうかね。
\(y\)方向の運動方程式を見ると、\(v_{x}\)が大きくなると、\(ev_{x}B\)が大きくなるの\(y\)方向の速度\(v_{y}\)はどこかで限界点を迎えそうというのがわかります。
本問題でもそのことに対する問いがありました。
初期条件も確認しておきましょう。
位置:\((x,y)=(0,0)\)
速度:\((v_{x},v_{y})=(0,0)\)
変数が\(v_{x},v_{y}\)の、微分方程式の連立式を解くことになるので、きつそうです。
ですので、この場合は多くはエネルギー保存則を使うのではないかなと感じました。
静電ポテンシャルとローレンツ力による仕事
静電ポテンシャルによる仕事を使う場合は、例えば、
といった問題の時は、
として求めます。
では、ローレンツ力による仕事は?
ローレンツ力による仕事はゼロです。
これを知っておかないと今回の場合、「あれ?ローレンツ力による仕事ってどうやって計算するんだっけ?」ってなります。
なぜ、今まで気にしたことがなかったのかを20分経って思い出しました!!
そうだ、ローレンツ力は電子の移動する向きに対して常に直角だった!!
(「ローレンツ力」と「電子の速度」は外積なので・・・)
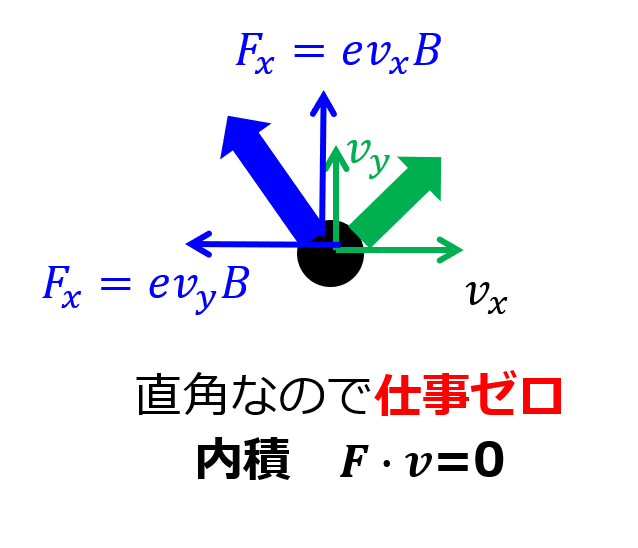

だから、ローレンツ力による仕事はゼロか(仕事なので、内積をとるとゼロ)!!ってことで、電場による静電ポテンシャルだけ考えればよかったのでした。
第3問:熱力学
第3問は熱力学の問題です。
この問題は、高校生にはきついかな~って感じがしました。
またまた、微分方程式ですよ。
僕の記憶だと、流体力学や熱力学を大学で学んだ時に例題として出されていました。
高さ\(z\)方向を変数とする圧力\(P(z)\)と数密度\(n(z)\)を求める問題
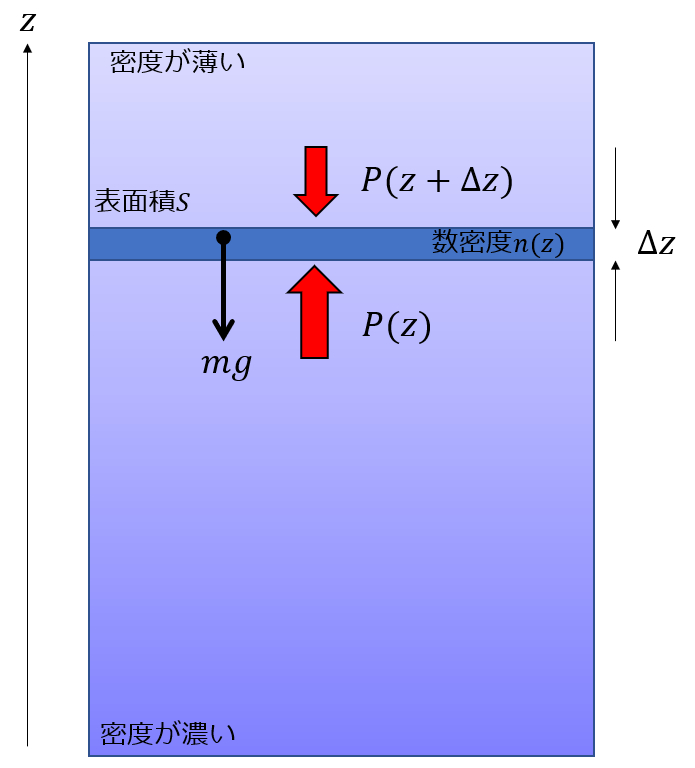

これもちゃんと自分の中に方針さえ決めて入ればさほどむずかしくありませんね。
熱力学の問題を解く際のポイント
- 力のつりあいを考える
- 熱力学第一法則で考える
- 理想気体の状態方程式を考える
この3つだけです。
求めるべく関数は、数密度\(n(z)\)と圧力\(p(z)\)です。
そして使うべき方程式は、
上記の「1.力のつり合い」「理想気体の状態方程式」だけでした。
1.力のつりあいより
※ここで、\(\Delta z\)区間の質量を\(m(z)=mn(z)S\Delta z\)
単原子分子1つあたりの質量が\(m\)
3.理想気体の状態
※\(k_{B}=\frac{R}{N_{A}}\):アボガドロ数\(N_{A}\)
(1)(2)式を使って、\(p(z)\)の微分方程式が出ます。
\(\Delta z → 0\)とすると、
となります。
この(4)式が、圧力に対する微分方程式ですね。
目標は、この(4)の微分方程式を解くことになります。
で、これは大学1回生の知識があれば解けますね。
そうですね(3)式を見ると、ちょっと「うっ」ってなりそうですね。
これくらいなら高校生でもできるのですが、そこは京都大学のやさしさ・・・・ちゃんと誘導問題になっていました!(^^)!
まとめ
修士卒の物理好きが京都大学の2018年の物理の問題を解いてみました。
感想は、「大学の知識であるけども誘導問題にすることで高校生でも十分に点数出来るだろうな~」っていう問題でした(‘ω’)
その他の過去問も見ましたが、高校生は初めて見るような問題が多いかなと思います。
けど、高校生の配慮をするために誘導が丁寧なのできっと高得点を取れる科目になるのではないかと思います(^^)/