こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
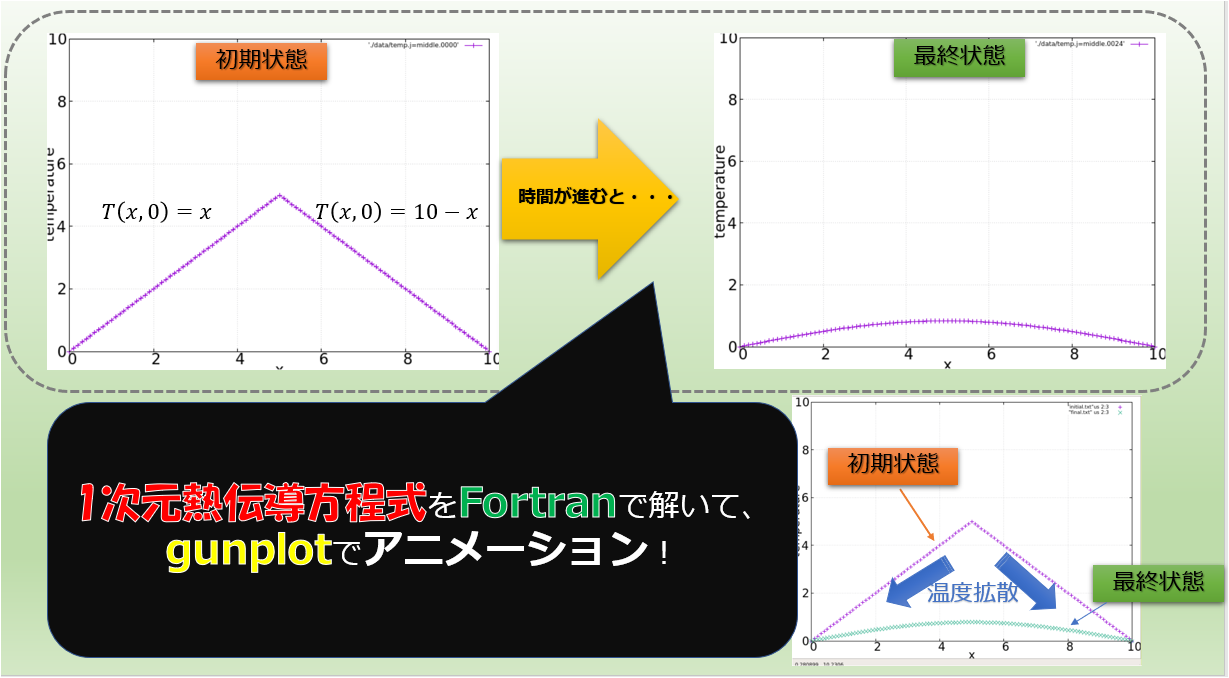
前回下記のような記事を出しまして、
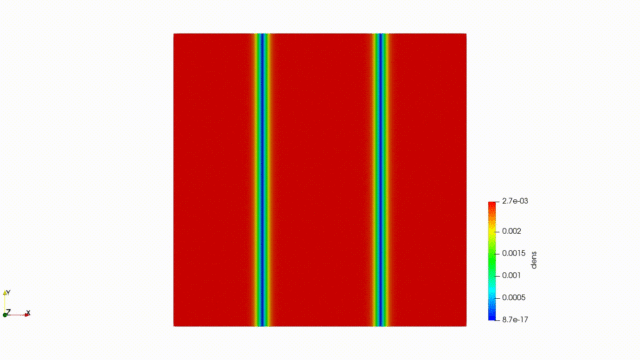
前回の記事で示したアニメーションはこんな感じ
カマキリ
1次元の熱伝導方程式のアニメーションを作ったのです
1次元グラフのアニメーションができるのならば、gnuplotの「splot」を使って3次元アニメーションも作れるなと思ったので、記事にします(^^)/
本記事の内容
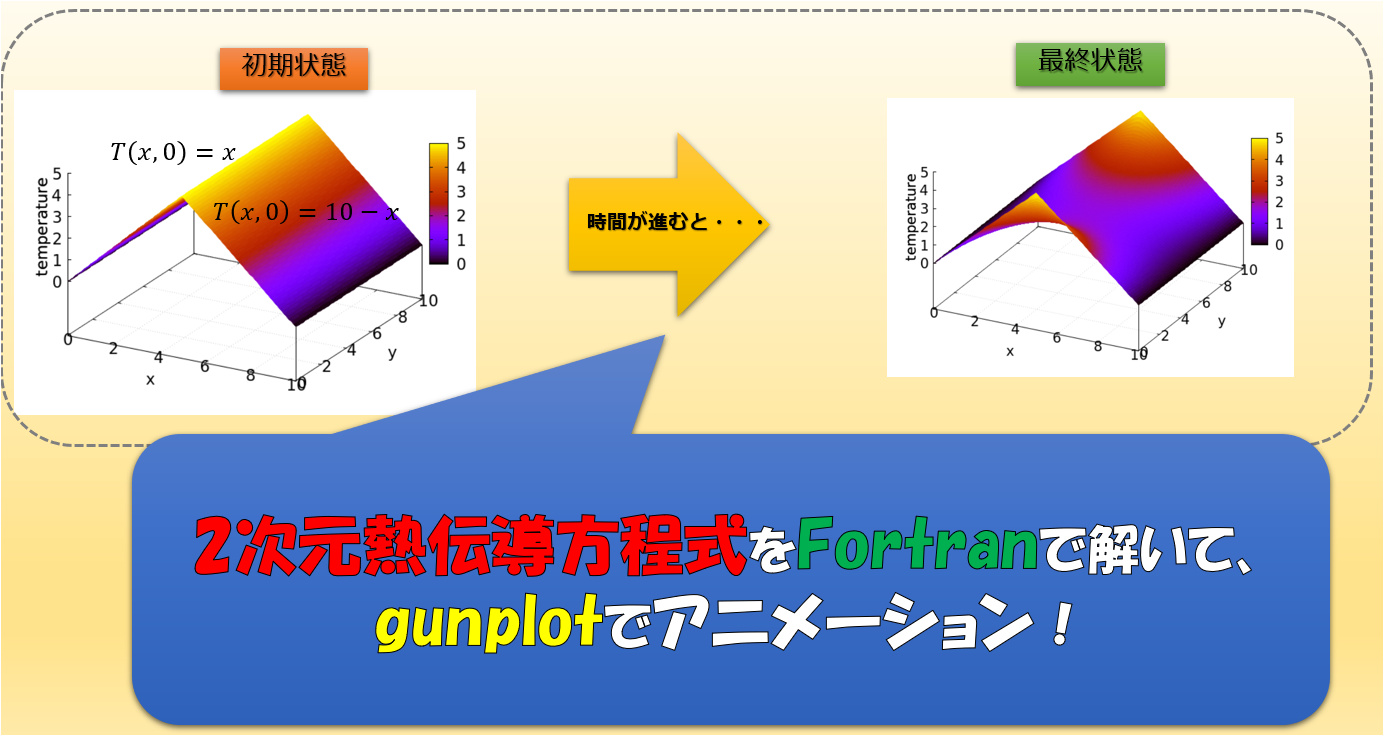
2次元の熱伝導方程式をFortranで解いて、gnuplotで3次元アニメーションを作る(^^)/
※Fortranのコードとスクリプトは本記事にアップされています。
※FortranのコードはFortran90/95の書き方にしているつもりですが正確に書けているかは不明です。
※FortranはWSLを使ってインストールしています。
※gnuplotはこのサイトを参考にすれば良いかと思います。
※FortranのコードはFortran90/95の書き方にしているつもりですが正確に書けているかは不明です。
※FortranはWSLを使ってインストールしています。
※gnuplotはこのサイトを参考にすれば良いかと思います。
僕の使用環境はWindows10でWindows Subsystem for Linux（WSL）を使って、UbuntuからFortranやgnuplotをインストールして使用しています。
カマキリ
説明がくどいな～って思った方は「まとめ」へGo！！
2次元熱伝導方程式をFortranで解く
まずは解くべき方程式を明らかにしておきましょう。
2次元熱伝導方程式
\begin{align*}\frac{\partial T}{\partial t}=\kappa\bigg(\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}\bigg)\tag{1}\end{align*}
熱伝導方程式は、初期状態を与えれば(1)式に従って時間発展をする方程式です。
今回は初期状態を以下のようにしておきます。
中央だけ中央だけ温度が高く、\(x\)方向の両端は温度０(K)の条件となっています。
また、\(x\),\(y\)の端は初期状態から変化させないような境界条件にしているので、時間発展させると中央の高い温度の部分から低い温度へ熱移動が生じて、下記のような変化を示します。
今回は、これをgnuplotを使ってアニメーションを作ろうということになります。
全体の流れ
アニメーション作成までの全体の流れを押さえておくと少し気持ちのハードルは下がるかもしれないので、先に全体の流れを示しておきます。
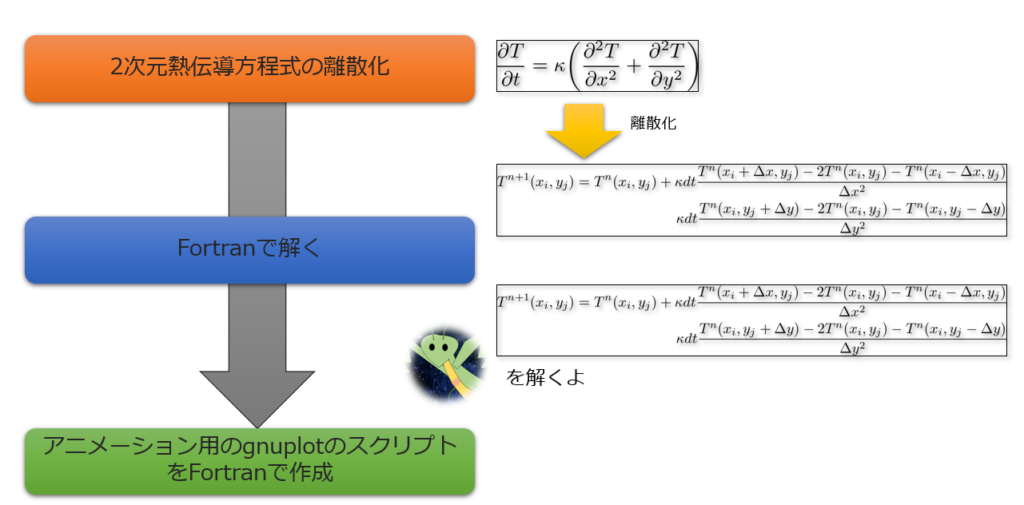
- 2次元熱伝達方程式は偏微分方程式であるため、それを数値的に解くためには離散化してあげる必要があります。
今回は、「時間に対しては陽解法」「空間に対しては2次精度」で解くことを考えています。 - 次にForranを使って離散化した方程式を数値的に解くことを考えます。
（※コードは後ほど） - Fortranで出力したデータをgnuplotで順番に読み込んでいくためのスクリプトをFortranを使って作成します。
これらのことができれば、あとはgnuplotで「3.」で作成されたスクリプトを実行するだけアニメーションを作成することができます。
※1次元熱伝導方程式を題材にしたのは、簡単な方程式の方がアニメーション作成の方法を理解しやすいと思ったからです。
ゆえに、離散化も特にこだわってはいません。
2次元熱伝導方程式の離散化
2次元熱伝導方程式
\begin{align*}\frac{\partial T}{\partial t}=\kappa\bigg(\frac{\partial^2T}{\partial x^2}+\frac{\partial^2T}{\partial y^2}\bigg)\tag{1}\end{align*}
この偏微分方程式を離散化するにあたって、
- 時間微分の項（左辺）は陽解法
- 空間微分の項（右辺）は2次精度
で離散化で進めていきましょう。
離散かされた式が↓こちらです。
\begin{align*}T^{n+1}(x_{i},y_{j})=T^{n}(x_{i},y_{j})+\kappa dt\frac{T^{n}(x_{i}+\Delta x,y_{j})-2T^{n}(x_{i},y_{j})-T^{n}(x_{i}-\Delta x,y_{j})}{\Delta x^2}\\
\kappa dt\frac{T^{n}(x_{i},y_{j}+\Delta y)-2T^{n}(x_{i},y_{j})-T^{n}(x_{i},y_{j}-\Delta y)}{\Delta y^2}\end{align*}
\kappa dt\frac{T^{n}(x_{i},y_{j}+\Delta y)-2T^{n}(x_{i},y_{j})-T^{n}(x_{i},y_{j}-\Delta y)}{\Delta y^2}\end{align*}
では、これをFortranで解きましょう(^^)/
Fortranで解く
離散化された方程式をFortranで解くためのプログラムを書いていきましょう。
以下がプログラムです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 | !ファイル名 2D_Thermal_Eq.f90 module constants implicit none integer::i,j,nt integer, parameter :: imax = 100,jmax=imax,ntmax = 2500 real(8):: T(0:imax,0:jmax),xmax,ymax,x,y,dx,dy,dt,kp integer,parameter :: SP = kind(1.0) integer,parameter :: DP = selected_real_kind(2*precision(1.0_SP)) end module constants module print use constants implicit none contains subroutine print__profile(f) real(DP), dimension(0:imax,0:jmax), intent(in) :: f integer :: counter = 0 character(len=*), parameter :: base = "./data/temp.j=middle." character(len=4) :: serial_num character(len=40) filename write(serial_num,'(i4.4)') counter write(filename,"(a,i5.5,a)") base//serial_num open(10,file=filename) do j=0,jmax do i = 0 ,imax write(10,"(2f10.4,2f10.4,2f10.4)") i*dx, j*dx,f(i,j) end do write(10,"(2f10.4,2f10.4,2f10.4)") end do close(10) counter = counter + 1 end subroutine print__profile end module print program thermal_explicit use constants use print implicit none dt = 0.004 kp = 1 xmax = 10 ymax=xmax dx = xmax/imax dy = ymax/jmax open(10,file="initial.txt") open(11,file="final.txt") !initial state do j=0,jmax do i = 0, imax x = dx*i y = dy*j if (i < imax/2) then T(i,j) = x else T(i,j) = xmax - x endif write(10,*) ,x,y,T(i,j) end do end do call print__profile(T(:,:)) !Time step do nt = 1, ntmax do j=1,jmax-1 do i = 1, imax-1 T(i,j) = T(i,j) + kp*dt/(dx*dx)*(T(i+1,j)- 2*T(i,j) +T(i-1,j)) & + kp*dt/(dy*dx)*(T(i,j+1)- 2*T(i,j) +T(i,j-1)) end do end do if (mod(nt,100)==0) call print__profile(T(:,:)) write(*,*)nt end do !Final state do j=0,jmax do i = 0, imax x = dx*i y = dy*j write(11,*) x,y,T(i,j) end do end do end program thermal_explicit |
↓前回の記事の次元を1次元から2次元に拡張しただけです。
↑今回はgnuplotの3次元表示のsplotでの表示の仕方をpm3d（カラーマップ表示）でしたかったのですが、上記のようにプロットするデータは同じ数字が続いている場合には改行をいれないといけないようでして、改行を入れるようにプログラムを書いています。
↑ちなみに「data」という名前のディレクトリを自分で作っておく必要があります。
以上がプログラムの中身です。
ここまでできたら、以下のコマンドで計算を実行させます。
1 2 | gfortran 2D_Thermal_Eq.f90 ./a.out |
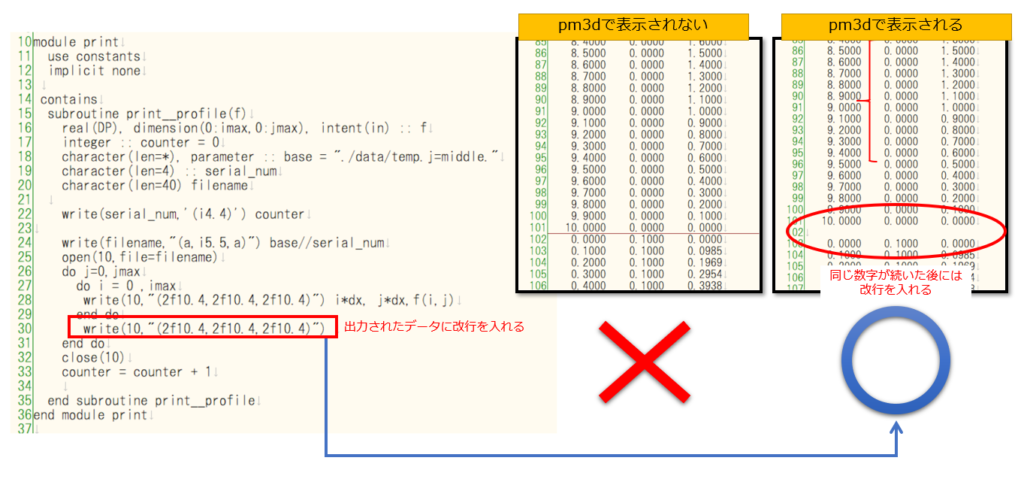
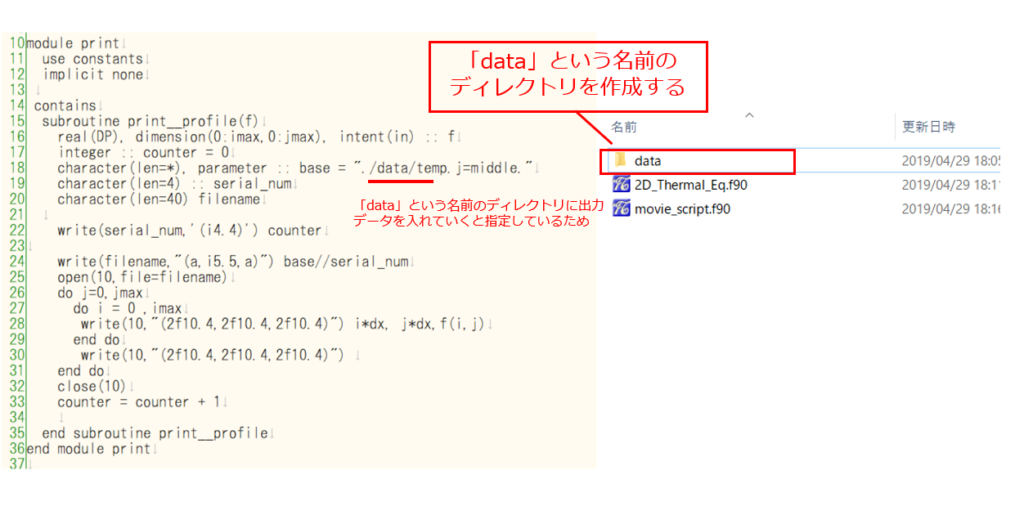
実行ができれば「data」という名前のディレクトリの中に、以下のように大量のデータが保存されていることが確認できます。
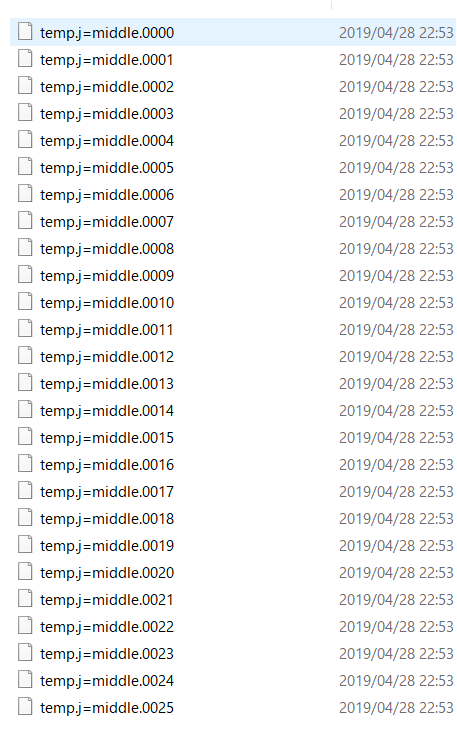
これらのデータが指定したタイムステップで出力された温度の空間分布のデータです。
あとは、これらのデータを順番にgnuplotで読み込めばアニメーションが完成ということになります。
そのためには、gnuplotのスクリプトが必要になります。
スクリプトは書くのが少々面倒なので、スクリプト自体をFortranで書くことにします。
アニメーション用のgnuplotのスクリプトをFortranで作成
gnuplotのスクリプトを作成するためのFortranのプログラムがこちらです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | program animation_script implicit none integer, parameter :: imax = 100,xmax = 10,ymax=xmax integer :: counter, counter_end = 24,dx character(len=*), parameter :: base='./data/temp.j=middle.' character(len=4) :: serial_num dx = xmax/imax print *, "#" print *, "# gnuplot script generated by movie_script.f90" print *, "#" print *, " " print *, "set xlabel 'x' # x-axis" print *, "set ylabel 'y ' # y-axis" print *, "set zlabel 'temperature' # z-axis" print *, "set xrange[0:", xmax, "] # j-grid min & max" print *, "set xrange[0:", ymax, "] # j-grid min & max" print *, "set yrange[0.0:10.0] # temperature min & max" print *, "set grid" print *, "set xlabel font 'Arial,20' " print *, "set ylabel font 'Arial,20' " print *, "set zlabel font 'Arial,20' " print *, "set tics font 'Arial,20'" print *, "set zlabel rotate by 90" do counter = 0 , counter_end write(serial_num,'(i4.4)') counter print *, "splot '"//base//serial_num//"' with pm3d" if ( counter==0) then print *, "pause 2" else print *, "pause 1" end if end do print *, "pause -1" end program animation_script |
↑簡単に説明すると「do文」のところで先ほどの「data」という名前のディレクトリ内の大量のデータを順番に読み込む作業を行っています。
では、以下のコマンドを実行してみます。
1 2 | gfortran movie_script.f90 ./a.out >movie |
「./a.out >movie」とするとmovieというファイルが出来上がり、その中にFortranの「print文」の内容を全て書き出してくれます。
この「movie」というファイルがgnuplotのスクリプトとなります。
以上のことが終えれば、あとはgnuplotで「movie」という名前のスクリプトを走らせるだけです。
アニメーションを作成してみよう(^^)/
「movie」というスクリプトは2通りの方法で実行できます。
方法１
↑このようにコマンドを打っても良いですし、
方法2
↑このように「gnuplot」と打って、「load “movie”」とスクリプトファイルをloadしても良いです。
アニメーションはこんな感じ
カマキリ
できた
まとめ
ごちゃごちゃ説明してしまいましたが、下記のzipファイルを解凍して下記のコマンドを打ってお試しください。
1 2 3 4 5 | gfortran 2D_Thermal_Eq.f90 ./a.out gfortran movie_script.f90 ./a.out >movie gnuplot movie |
数値計算のためのFortran90/95プログラミング入門(第2版)・アンサーブック: 演習問題の解答と解説
牛島 省
1,487円(04/19 06:40時点)
発売日: 2022/11/07
Amazonの情報を掲載しています
Follow @t_kun_kamakiri