こんにちは（@t_kun_kamakiri）(‘◇’)ゞ
先日、名古屋市科学館に行った際に、面白いものを見つけました。
2つの球を初期の高さを変えて同時に静かに離すと、どちらが先に最下端に到達するか？
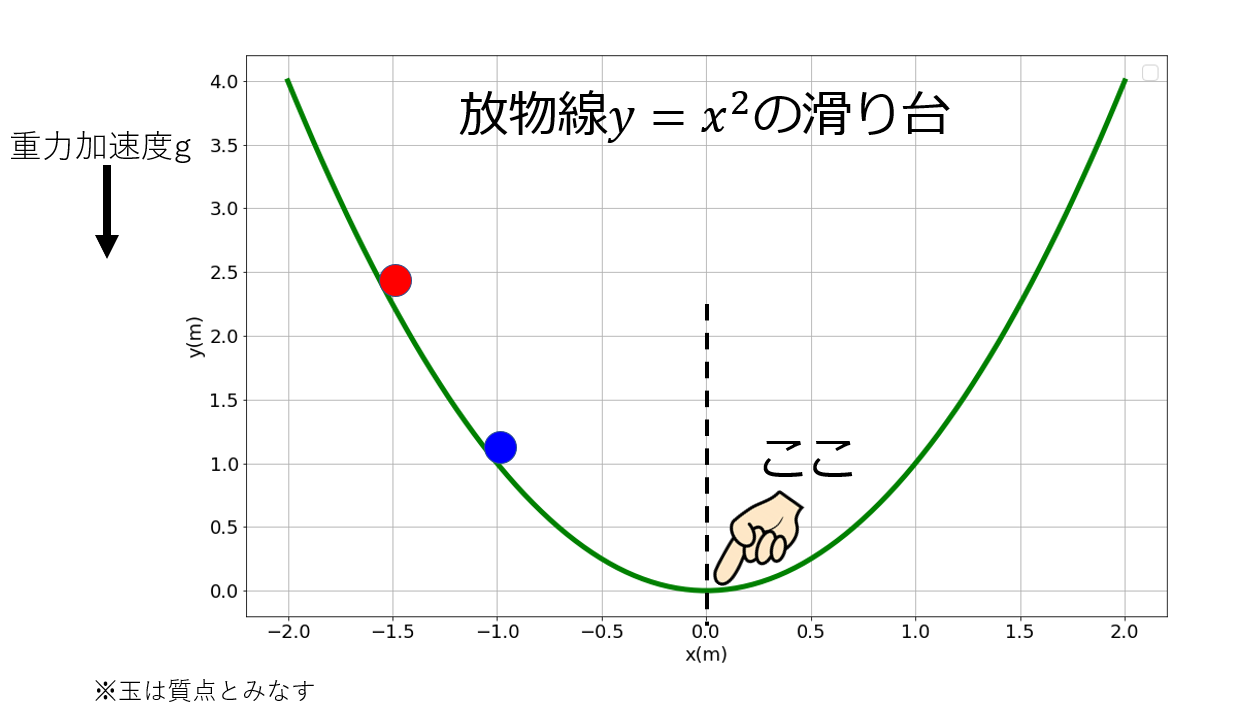
実際に肉眼で見ると高さ0の位置で両者同じ時間に通過している（？）ように見えたのです。↓こんな感じ。
？
どうなの(・・? pic.twitter.com/tSR1lEr3BM— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) October 18, 2021
動画を撮って撮影しましたがよく見ると青い球（初期高さが低い方）が先に最下端に来ているように見えます。
というわけで、Twitterでアンケートを取りました。
(?, ?)
— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) October 18, 2021
アンケート結果は、初期高さが違っても到達する時間は両者同じという方が大半ですね。
実際はどうなっているのか理論で説明できるのかを考えたいと思います。
- 球は質点とみなす
- 空気抵抗は考えない
- 摩擦もなし
- 放物線$y=\frac{1}{2}x^2$上を運動
本記事を読むにあたって解析力学の初歩的な知識は前提となります。
ラグランジュ方程式と束縛条件
球体の時刻歴を知るためには運動方程式を導く必要があります。
一般的に独立変数として座標$x,y$として考えますが、今回は球は放物線上を運動するため$x,y$は互いに独立ではない変数となります。そのため、その拘束力も考慮した運動方程式を考える必要があります。
この拘束力を考えるのが厄介なので、以下のラグランジアンと束縛条件から$x$に対する運動方程式を立てることを考えます。
ラグランジアン
- 運動エネルギー:$T=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)$
- ポテンシャルエネルギー:$U=mgy$
- 束縛条件:$y=\frac{1}{2}x^2$
放物線を$y=\frac{1}{2}x^2$として$\frac{1}{2}$の係数を付けて考えるのは、最終的な式の形がシンプルになるためです。
今回のように$x,y$は独立ではなく$h(x,y)=-\frac{1}{2}x^2+y=0$のような拘束条件をホロノミックな拘束条件といいます。
また、このような系をホロノーム系といいます。
$x,y$は独立ではなく束縛条件により$y$の動きは$x$によって規制されているので、どちらか片方の変数だけを考えれば良く、本記事では考えやすい$x$を変数として運動方程式を導出します。
オイラーラグランジュ方程式から運動方程式を導出
$y=\frac{1}{2}x^2$から$\dot{y}=\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}=x\dot{x}$となり、ポテンシャルエネルギーは$U=mgy=\frac{1}{2}mgx^2$となります。
よって、ラグランジアンは、
&=\frac{1}{2}m\big(\dot{x}^2+(x^2\dot{x}^2)\big)-\frac{1}{2}mgx^2\\
&=\frac{1}{2}m\big(1+x^2\big)\dot{x}^2-\frac{1}{2}mgx^2\tag{2}\end{align*}
オイラーラグランジュ$\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=\frac{\partial L}{\partial x}$から運動方程式を導出するにあたって以下を計算しておきます。
- $\frac{\partial L}{\partial \dot{x}}=m(1+x^2)\dot{x}$
- $\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=2mx\dot{x}+m(1+x^2)\ddot{x}$
- $\frac{\partial L}{\partial x}=mx\dot{x}^2-mgx$
よって、オイラーラグランジュ$\frac{d}{dt}\frac{\partial L}{\partial \dot{x}}=\frac{\partial L}{\partial x}$より、
2mx\dot{x}+m(1+x^2)\ddot{x}&=mx\dot{x}^2-mgx\\
\Leftrightarrow\\
(1+x^2)\ddot{x}&=-x\dot{x}^2-gx\tag{3}\end{align*}
運動方程式を導くことができました。
ここまで来たら解析解を導きたいですが、どうやら楕円積分など導入する必要があり解が簡単に出てきそうにありません。
次回は、ひとまず運動方程式を以下の形にして数値計算により結論を得たいと思います。
\ddot{x}=-\frac{x}{1+x^2}\dot{x}^2-\frac{g}{1+x^2}x\tag{4}\end{align*}
時間積分は4次のルンゲクッタを用いて解きます。
次回、お楽しみに(‘ω’)ノ
まとめ
今回は放物線上を運動する球はどちらの高さが先に最下端に到達するのかを考えました。
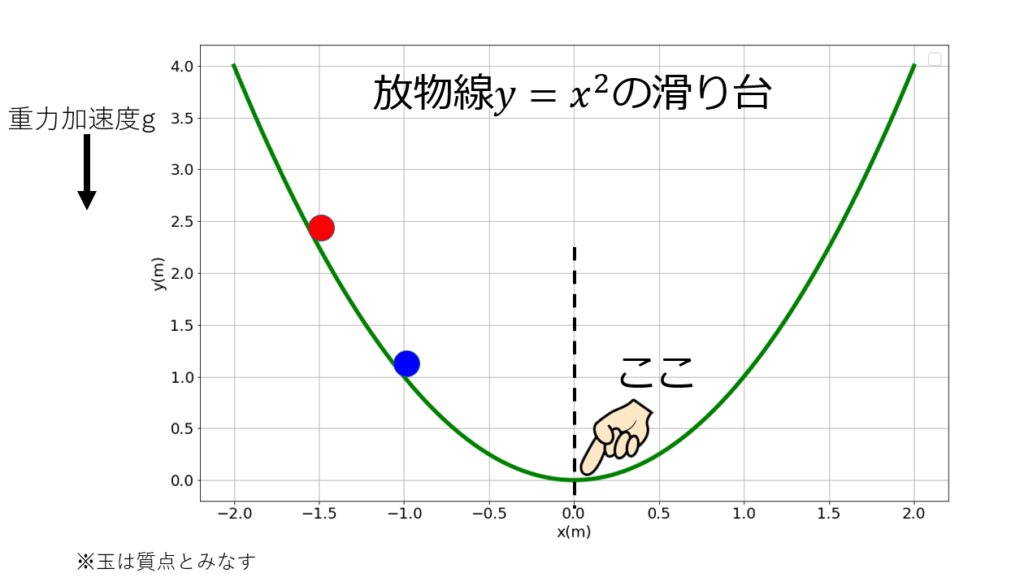
運動方程式は$(1+x^2)\ddot{x}=-x\dot{x}^2-gx$となることが、結論はまだ出ていません。
次回、放物線上の運動方程式の解析解を導きたいと思います。
のちに数値計算結果も載せます。
Follow @t_kun_kamakiri