こんにちは(@t_kun_kamakiri)(‘◇’)ゞ
本記事は前回の続きとなります。
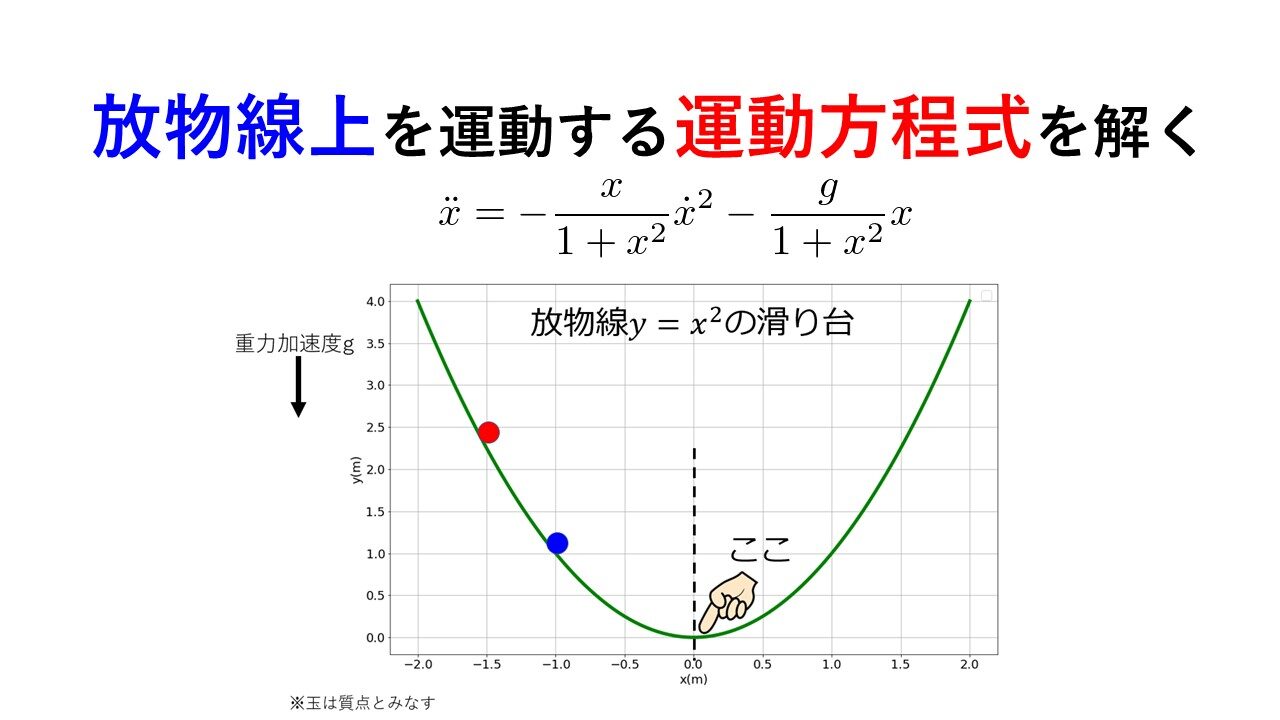
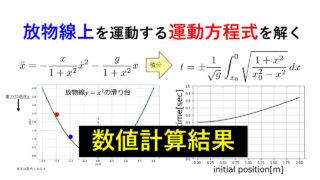
前回は以下のお題を出し、放物線上を運動する球の運動方程式を導出しました。
内容をさらっと振り返っておきましょう。
2つの球を初期の高さを変えて同時に静かに離すと、どちらが先に最下端に到達するか?
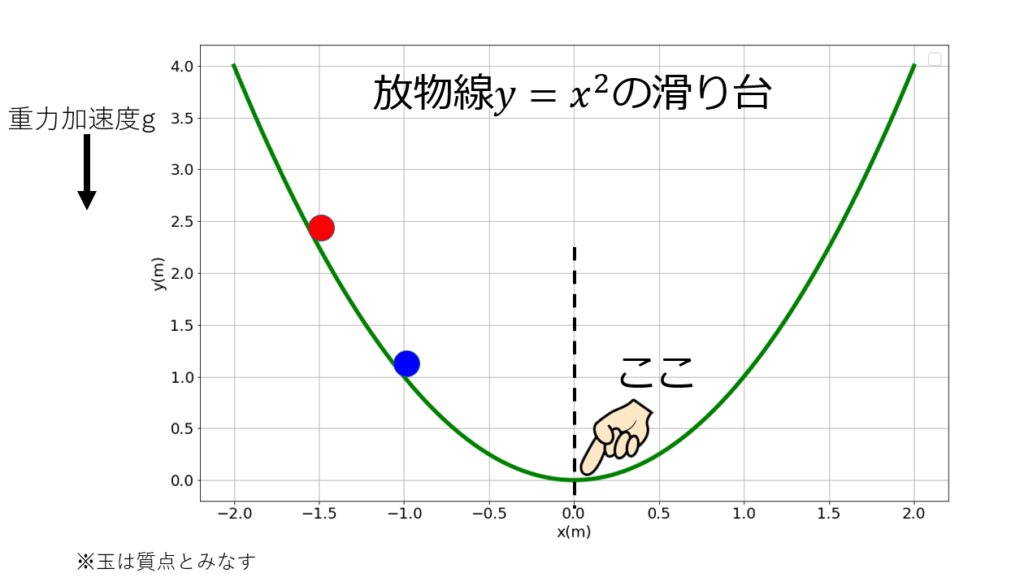
- 球は質点とみなす
- 空気抵抗は考えない
- 摩擦もなし
- 放物線$y=\frac{1}{2}x^2$上を運動
運動方程式は以下となりました。
(1+x^2)\ddot{x}&=-x\dot{x}^2-gx
\end{align*}
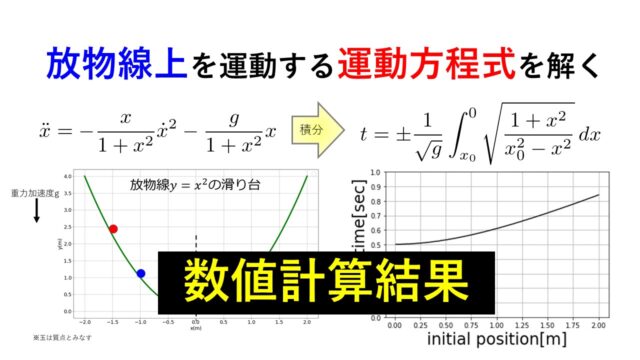
本記事はこちらの運動方程式を解析的に解くための導出過程を記します。
運動方程式の時間積分
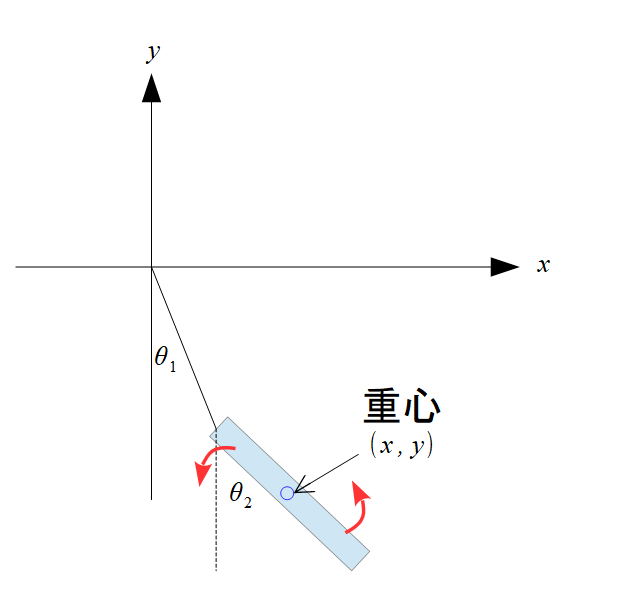
再度、放物線上を運動する運動方程式を書いておきます。
(1+x^2)\ddot{x}&=-x\dot{x}^2-gx\tag{1}
\end{align*}
こういった2階微分と1階微分がある微分方程式を解くにあたって合成微分を使うとうまく解くことができます。
(1)を以下のように整理します。
\frac{1}{g+\dot{x}^2}\ddot{x}&=-\frac{x}{1+x^2}\tag{2}
\end{align*}
左辺は$f(\dot{x})\ddot{x}$の形ができたので、時間積分するにあたって$\int f(\dot{x})\frac{d\dot{x}}{dt}dt=\int f(\dot{x})d\dot{x}$ と考えれば、$f(\dot{x})\ddot{x}$時間積分は$f(\dot{x})$を$\dot{x}$で積分した結果と同じになりますね。
右辺も同じような形を出しつつ左辺を計算しやすいようにするため、(1)の両辺に$2\dot{x}$を掛けます。
\frac{2\dot{x}}{g+\dot{x}^2}\ddot{x}&=-\frac{2x}{1+x^2}\dot{x}\tag{3}
\end{align*}
右辺も左辺と同じような形にできました。
よって、(3)を以下のように微分の形で書くことができます。
\frac{d}{dt}\log (g+\dot{x}^2)=\frac{d}{dt}\log (1+x^2)\tag{4}
\end{align*}
では(4)を時間積分しましょう。
\log (g+\dot{x}^2)=-\log (1+x^2)+C_{1}\tag{5}
\end{align*}
結果は$f(\dot{x})=\frac{2\dot{x}}{g+\dot{x}^2}$を$\dot{x}$で積分したことになりますね。$C_{1}$は積分定数です。
次に、対数を指数に置き換えると
g+\dot{x}^2&=e^{C_{1}}e^{-\log (1+x^2)}\\
&\Leftrightarrow\\
g+\dot{x}^2&=C(1+x^2)^{-1}\tag{6}
\end{align*}
ここで、$C=e^{C_{1}}$と置きました。
また$e^{\log a}=a$であることを使いました。対数の逆関数が指数なので元に戻ったということです。
初期条件を課して積分定数を求める
初期条件を課すことで積分定数が求まります。
- 初期位置:$x(0)=x_{0}$
- 初速度:$v(0)=\dot{x}(0)=0$
よって、
g&=C(1+x_{0}^2)^{-1}\\
&\Leftrightarrow\\
C&=g(1+x_{0}^2)\tag{7}
\end{align*}
積分して時刻を求める
(6)をもう少し整理しましょう。
\dot{x}&=\pm \sqrt{\frac{C-g(1+x^2)}{1+x^2}}\\
&\Leftrightarrow\\
\frac{dx}{dt}&=\pm \frac{1}{\sqrt{g}}\sqrt{\frac{x_{0}^2-x^2}{1+x^2}}\tag{8}
\end{align*}
(8)を変数分離して積分すると以下となります。
t=\pm\frac{1}{\sqrt{g}}\int^{x}_{x_{0}} \sqrt{\frac{1+x^2}{x_{0}^2-x^2}}\, dx\tag{9}
\end{align*}
(9)をゴリゴリ手計算して結果を出せればいいですね・・・・
ちょっとしんどそうなのでwolfram alphaさんにひとまず計算を任せてみました。

どうやら第2種楕円積分を使って求めることができるようです(‘ω’)
t=\pm\frac{1}{\sqrt{g}}\frac{x_{0}\sqrt{\frac{x^2+1}{x_{0}^2-x^2}}\sqrt{1-\frac{x^2}{x_{0}^2}}E\bigg(\sin^{-1}\big(\frac{x}{x_{0}}\big)|-x_{0}^2\bigg)}{\sqrt{x^2+1}}\tag{10}
\end{align*}
(10)の結果の係数のほとんどが約分できますね。
なので、もう少しきれいにまとめることができます。
t=\pm\frac{1}{\sqrt{g}}E\bigg(\sin^{-1}\big(\frac{x}{x_{0}}\big)|-x_{0}^2\bigg)\tag{11}
\end{align*}
どのように導出するかはTwitterに画像をアップしておきました。
第二種楕円積分
放物線上の質点の運動 pic.twitter.com/oFzPbVhUjW— カマキリ🐲Python頑張る昆虫 (@t_kun_kamakiri) November 4, 2021
Twitter上でも議論が続いています。
でもまだ少しよくわからないのが、プロットしてみるとこうなるんですよね。
横軸初期位置、縦軸最下部までの時間で、2つあるのは絶対値とれば連続になるからいいとして、x=0のときなんで0秒じゃないんだ?って… pic.twitter.com/uXpeGLInEh— ラジオ( r ・ω)r (@Freufirst) November 4, 2021
まとめ:運動方程式の結果
運動方程式$(1+x^2)\ddot{x}=-x\dot{x}^2-gx$の解は以下であることがわかりました。
積分した結果は以下です。
t=\pm\frac{1}{\sqrt{g}}E\bigg(\sin^{-1}\big(\frac{x}{x_{0}}\big)|-x_{0}^2\bigg)\tag{11}
\end{align*}
途中計算機に丸投げして結果を得ましたが、追々自力で(10)を導きたいと思います(‘ω’)ノ