こんにちは(@t_kun_kamakiri)(^^)/
大学物理に憧れて、力学を学習し始める人のために(挫折をしないように)、この教科書には気をつけろという代表作、ランダウ・リフシッツ(理論物理学教程)!!
この本は、有名で何度読んでも素晴らしいと言っていい本・・・・
ですが、いきなり読む多くの人が挫折します。
なぜか??
結論から入ってやりました。
しかし、誤解しないでください。
ランダウ=リフシッツ(理論物理学教程)はとても素晴らしい書籍です。
あなたの物理のレベルは揺るぎないものになるはずです。
ランダウ=リフシッツ(理論物理学教程)は素晴らしい教科書なのですが、いきなり読んだらだいたい無残に散ります(笑)
ですが、読むとすごい教科書であることに気が付きます。
本記事では「なぜこの本をいきなり読むと挫折するのか?」を説明したいと思います。
解析力学を勉強して記事にまとめました。
目次:解析力学
ランダウは名著ではなりますが、せっかく読み始めたのに読めないのですよね。
何度読んでも新たな気づきがあったり、知らなかった知識が増えたりと素晴らしい本ですので、ぜひ挑戦してほしいです。
自分自身も学生時代を思い出しながら、解析力学を勉強しなおしました。
当ブログによって、初学者のハードルを下げれたらと思っています(^^)
大学の物理学科で習う内容
ところで、大学の理学部の物理はいったい何を学ぶところかと言いますと。。
こんなところでしょうか。
そして、まず一番最初に確実に「力学」を学習します。
「力学」は上記の分野において、とても基本的な分野であって高校生・大学生問わず必ず一番最初に習うのです。
そこで学習するにあたって、大学の授業だけ聞いていても身に着くことは授業以上には期待できないので、多くの学生は自ら参考書を選び学習することかと思います。
そこで、有名な参考書として、「ランダウ=リフシッツ(理論物理学教程)」を手に取るケースがあると思います。
それは先生の勧めであったり、先輩の勧めであったり、ネットの情報であったり・・・
しかし、注意が必要です。
それらの「本を勧めてくれた人」はある程度物理を学んだ後の人、つまりはもう既に変態なのです。
↓この「力学」というのを見て、皆さんどのように思われますか?
簡単な「力学の入門書」に見えますよね?
これだけ見ると初学者向けの入門書のように見えてしまいますが、これをいきなり読むと・・・・これが、まーーーよくわからない(*_*;
なぜよくわからないのか??
力学でも特に高度な内容だからか??
・・・違うのですよね・・・・
それは次のことから来ています。
ランダウ=リフシッツの力学は解析力学
そうです。
この「力学」に釣られて購入した初学者の人は、これが「力学」か??と思うのですが、これは解析力学の教科書です。
まず、「解析力学」と「力学」は少々立ち位置が違います。
一般的な「力学」の立ち位置は、
- 第一法則:慣性の法則
物体が力を受けていない場合、静止しているものは静止し続け、運動しているものは等速直線運動を続ける。 - 第二法則:運動方程式\(ma=F\)
物体が力の作用を受けるときは、その力の向きにその大きさに比例した加速度が生じる。 - 第三法則:作用反作用の法則
物体が他の物体から力を作用させるとき、その力の向きにその物体から同じ大きさで反対向きに反作用を受ける。
力学は上記の第三法則をもとに、運動方程式を立てて物体の運動を予測する問題を取り扱うというものです。
一方、「解析力学」は次のような立ち位置を取っています。
ニュートン力学をより美しく一般的な形式に従って運動を記述できるようにした学問であると言えます。
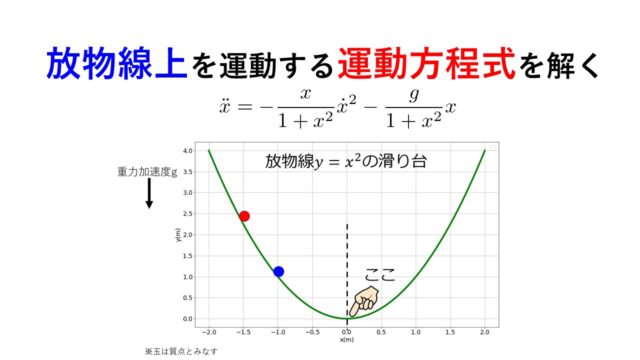
例えば・・・運動方程式を記述する場合において、デカルト座標系\((x,y,z)\)で記述する場合と、極座標系\((r,\phi,\theta)\)で記述する場合とで、運動方程式の形が全く変わってしまいます。
しかし、もっと一般的な座標系でもそれらが統一された、一般的な形式で書ける方法を示したのが、解析力学の学問のスタートになっています。
ですので、解析力学の内容である「ランダウ・リフシッツの力学」の教科書でも、
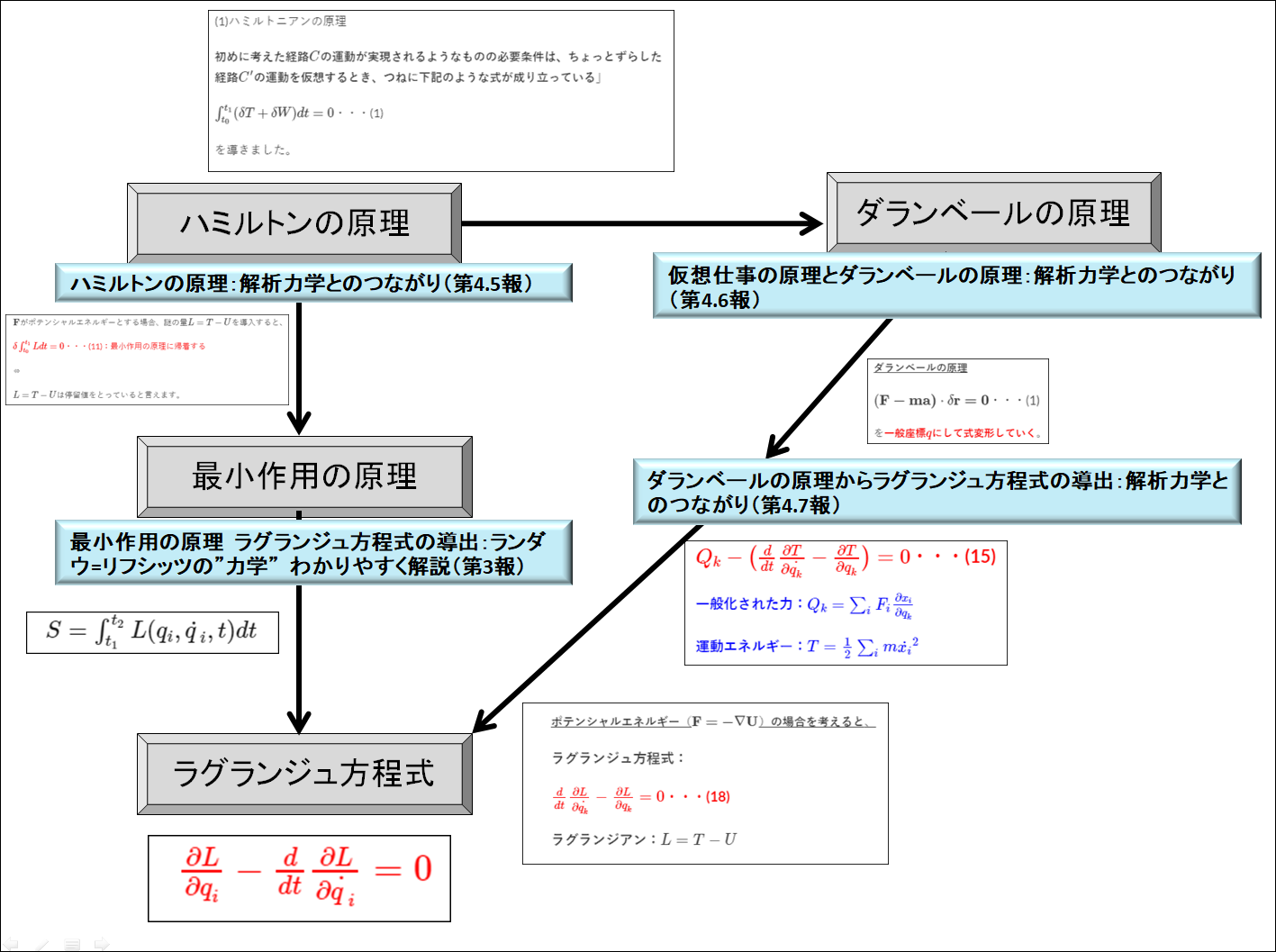
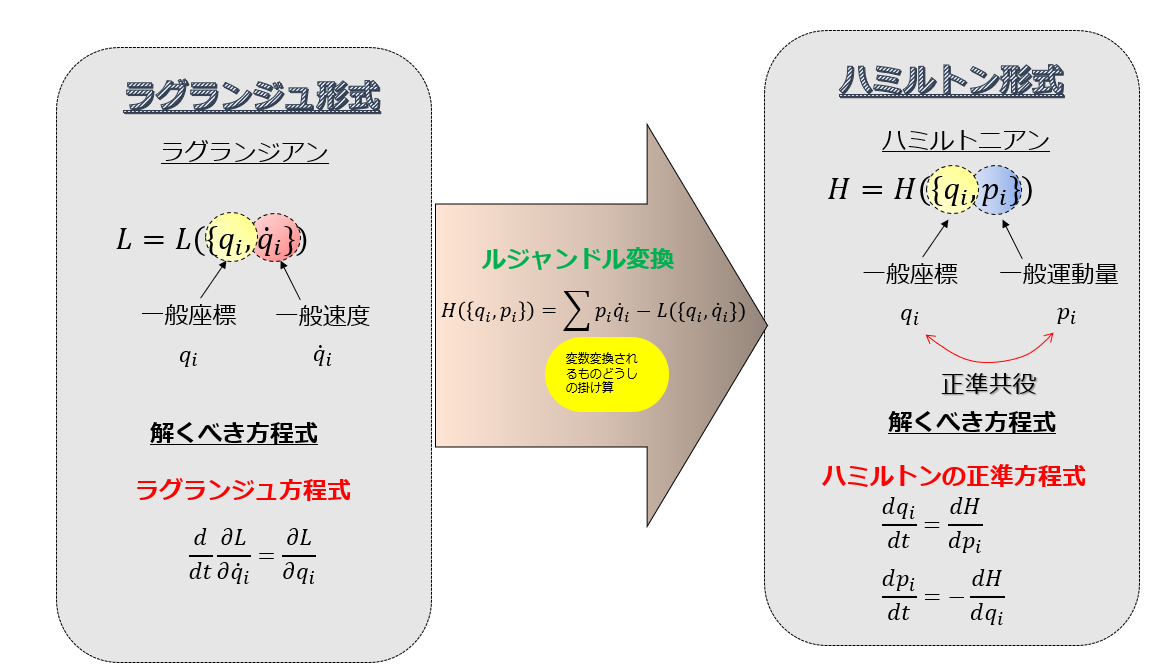
ラグランジアン\(L\)を導入
↓
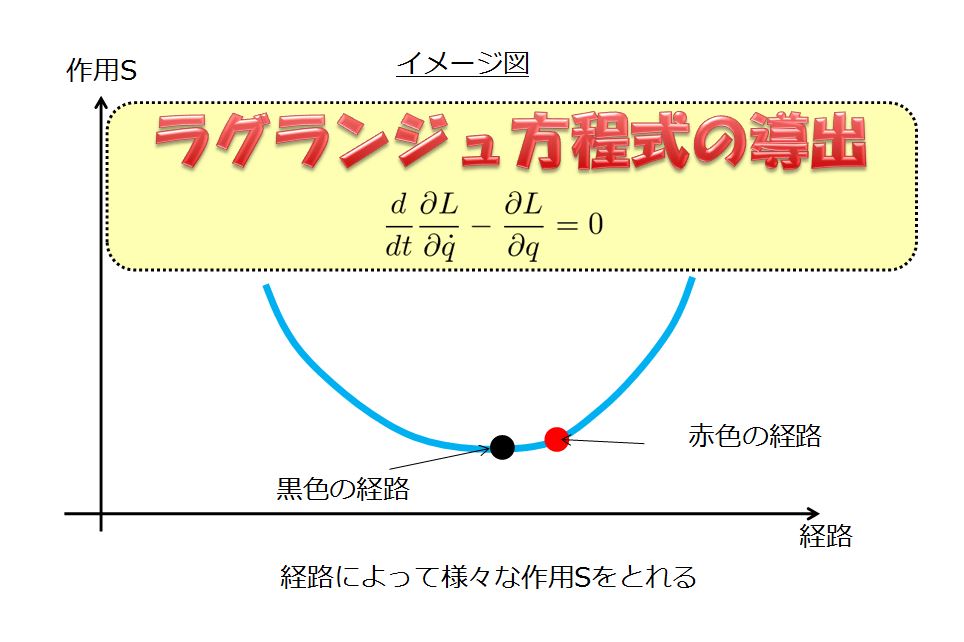
オイラー・ラグランジュ方程式
ラグランジアン\(L\)が見つかれば、オイラー・ラグランジュ方程式に代入することで、問題としている基礎方程式をあっさり導けるので、そんなに覚えることも少なくて楽なのです。
デカルト座標系\((x,y,z)\)でも、極座標系\((r,\theta,\psi)\)でも同じように、1本のラグランジュ方程式で記述できるなんて。
もっと深く内容を追っていきたかったのですが、記事を書くだけでめちゃくちゃ時間がかかってしまいました。あと、内容を理解するために読み漁るのも時間がかかります。
ですので、こちらをシリーズ化することを考え、読みながら随時記事をアップしていきたいと思います。
本日は、「ランダウ=リフシッツ(理論物理学教程)」の”力学”は”解析力学”ですよ!!
という記事でした。
次回は、ラグランジュ方程式の導出にあたって必要な考え方である一般座標系↓のお話になります。
参考図書
解析力学:マセマキャンパスゼミ
↑こちらは「スバラシク実力がつくと評判」シリーズの解析力学の参考書です。
著者は高校数学を教える予備校の講師で、とてもわかりやすいと評判です。
解析力学ⅠⅡ:朝倉物理学大系
この2冊は解析力学の名著ですね。
詳解 力学演習
こちらは「力学」と「解析力学」の演習問題を扱っている演習問題集になります。





















コメント失礼します。二年ほど前に大学入る直前にランダウの力学を読んでみましたが、当時はいきなりラグランジアンが出てきてよく理解できませんでして、まさに記事のように挫折しました。今は大学で力学と解析力学をあらかじめ勉強してきて読むと、ランダウさんの本がすごくまとまっていると感じます。今はランダウさんの本をもとにもう一度解析力学を勉強していくつもりです。
お読みいただいてありがとうございます。
大学に入る前に読むのはすごいですね。
お読み頂いた記事は、ランダウを否定するつもりではなく、少々誤解を生む面があり、書きました。
解析力学も力学も大きなくくりでは、確かに力学なので、ランダウの力学はそういう意味では「力学」と言っても良いでしょうが、
難しさと思っている内容ではない(力学と思ったら解析力学から話を進めている)という点で挫折するという個人的な説です。
ランダウは行間を埋めるのがとても大変ですが、頑張ってください。