Step3:空間微分の離散化の定義
Diff1d.hに名前空間fdとして空間微分の定義を行います。
- gradX:x方向1階微分後退差分$\frac{\partial u}{\partial x}=\frac{u_{i,j}-u_{i-1,j}}{dx}$
- gradY:y方向1階微分後退差分$\frac{\partial u}{\partial y}=\frac{u_{i,j}-u_{i,j-1}}{dy}$
- gradXCDS:x方向1階微分中心差分$\frac{\partial u}{\partial x}=\frac{u_{i+1,j}-u_{i-1,j}}{2dx}$
- gradYCDS:y方向1階微分中心差分$\frac{\partial u}{\partial y}=\frac{u_{i,j+1}-u_{i,j-1}}{2dy}$
- poissonX:x方向2階微分中心差分$\frac{\partial^2 u}{\partial x^2}=\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{dx^2}$
- poissonY:y方向2階微分中心差分$\frac{\partial^2 u}{\partial y^2}=\frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{dy^2}$
Diff1d.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 |
#include <vector> #include "Fields.h" #include <cmath> //add using std::vector; namespace fd1d { // U U U U //*-----*----*----* // i-1 i Fields::vectorField1d gradX1d(Fields::vectorField1d& vec) //typedef vector<Fields> vectorField1d; { Fields::vectorField1d temp = vec; for (int i = 1; i < vec.size(); i++) { temp[i].value = (vec[i].value - vec[i - 1].value) / (vec[i].x - vec[i - 1].x); } return temp; } Fields::vectorField1d laplacianX1d(Fields::vectorField1d& vec) //typedef vector<Fields> vectorField1d; { Fields::vectorField1d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { temp[i].value = (vec[i + 1].value - 2.0 * vec[i].value + vec[i - 1].value) / pow((vec[i].x - vec[i - 1].x), 2.0); } return temp; } } namespace fd { Fields::vectorField2d gradX(Fields::vectorField2d& vec) { Fields::vectorField2d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { temp[i][j].value = (vec[i][j].value - vec[i - 1][j].value) / (vec[i][j].x - vec[i - 1][j].x); } } return temp; } Fields::vectorField2d gradY(Fields::vectorField2d& vec) { Fields::vectorField2d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { temp[i][j].value = (vec[i][j].value - vec[i][j - 1].value) / (vec[i][j].y - vec[i][j - 1].y); } } return temp; } Fields::vectorField2d gradXCDS(Fields::vectorField2d& vec) { Fields::vectorField2d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { temp[i][j].value = (vec[i + 1][j].value - vec[i - 1][j].value) / (2.0 * (vec[i + 1][j].x - vec[i - 1][j].x)); } } return temp; } Fields::vectorField2d gradYCDS(Fields::vectorField2d& vec) { Fields::vectorField2d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { temp[i][j].value = (-vec[i][j - 1].value) / (2.0 * (vec[i][j + 1].y - vec[i][j - 1].y)); } } return temp; } Fields::vectorField2d laplacian2d(Fields::vectorField2d& vec) //typedef vector<Fields> vectorField1d; { //Fields::vectorField2d temp(vec.size(), vector<Fields>(vec[0].size())); temp[i][j].x が空[0]になる Fields::vectorField2d temp = vec; //上書きする.もしくは参照渡しにする. for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[j].size() - 1; j++) { temp[i][j].value = (vec[i + 1][j].value - 2.0 * vec[i][j].value + vec[i - 1][j].value) / pow((vec[i][j].x - vec[i - 1][j].x), 2.0) + (vec[i][j + 1].value - 2.0 * vec[i][j].value + vec[i][j - 1].value) / pow((vec[i][j].y - vec[i][j - 1].y), 2.0); } } return temp; } Fields::vectorField2d lapOp(Fields::vectorField2d& vec) //typedef vector<Fields> vectorField1d; { //Fields::vectorField2d temp(vec.size(), vector<Fields>(vec[0].size())); temp[i][j].x が空[0]になる Fields::vectorField2d temp = vec; //上書きする.もしくは参照渡しにする. for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { double dxsq = pow((vec[i][j].x - vec[i - 1][j].x), 2.0); double dysq = dxsq; temp[i][j].value = ( (vec[i + 1][j].value + vec[i - 1][j].value) * dxsq + (vec[i][j + 1].value + vec[i][j - 1].value) * dysq ) / (2.0 * (dxsq + dysq)); } } for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { //std::cout << "temp[i][j].value = " << temp[i][j].value << std::endl; } } return temp; } Fields::vectorField2d poissonX(Fields::vectorField2d& vec) { Fields::vectorField2d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { double dxsq = pow((vec[i][j].y - vec[i][j - 1].y), 2); double dysq = pow((vec[i][j].x - vec[i - 1][j].x), 2); temp[i][j].value = (dysq * (vec[i + 1][j].value + vec[i - 1][j].value)) / (2.0 * (dxsq + dysq)); } } return temp; } Fields::vectorField2d poissonY(Fields::vectorField2d& vec) { Fields::vectorField2d temp = vec; for (int i = 1; i < vec.size() - 1; i++) { for (int j = 1; j < vec[i].size() - 1; j++) { double dxsq = pow((vec[i][j].y - vec[i][j - 1].y), 2); double dysq = pow((vec[i][j].x - vec[i - 1][j].x), 2); temp[i][j].value = (dxsq * (vec[i][j + 1].value + vec[i][j - 1].value)) / (2.0 * (dxsq + dysq)); } } return temp; } }// ene namespace fd |
こちらの微分の離散化を使ってmain.cppでステップ数の分だけ計算をしてみましょう。
解く方程式は以下です。
\begin{align*}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = \nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right) \tag{15}
\end{align*}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = \nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right) \tag{15}
\end{align*}
\begin{align*}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = \nu \left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2} \right) \tag{16}
\end{align*}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = \nu \left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2} \right) \tag{16}
\end{align*}
\begin{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2}=0 \tag{18}
\end{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2}=0 \tag{18}
\end{align*}
テスト計算なので流速ベクトル$\boldsymbol{u}$と圧力$p$は独立の式として解くようにしています。
main.cppでのステップ数のループは以下の部分です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
for (int nt = 0; nt < ntimestep; nt++) { cout << "Iteration no : " << nt << endl; //outcome if (nt % 10 == 0) { filewriter2d_.write2dUVFields(Unew, Vnew, Pnew, nt, name); } U = Unew; V = Vnew; P = Pnew; /* du/dt + udu/dx + vdu/dy= nu ∇^2 u dv/dt + udv/dx + vdv/dy= nu ∇^2 v */ Unew = U - dt * (U && fd::gradX(U)) - dt * (V && fd::gradY(U)) + dt * visc * (fd::laplacian2d(U)); Vnew = V - dt * (U && fd::gradX(V)) - dt * (V && fd::gradY(V)) + dt * visc * (fd::laplacian2d(V)); /* ∇^2 P = 0 */ Pnew = (fd::poissonX(P)) + (fd::poissonY(P)); //ポアソン方程式 } |
初期状態は以下としています。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
// initial condition for (int i = 0; i < U.size(); i++) { for (int j = 0; j < U[i].size(); j++) { if ((U[i][j].x > 0.75 && U[i][j].x < 1.25) && (U[i][j].y > 0.75 && U[i][j].y < 1.25)) { U[i][j].value = 2.0; } } } Unew = U; |
今回はUだけを計算して結果を確認します。
main.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
#include <iostream> #include <vector> #include "Mesh.h" //メッシュ設定 #include "Fields.h" //場の定義 #include "Diff1d.h" //空間微分 #include "FileWriter.h" //ファイル出力 #include "PrintVector.h" //場のprint文 using namespace std; using std::vector; int main() { int nx = 20, ny = 20; double lengthx = 2.0, lengthy = 2.0; Mesh mesh2d_(nx, ny, lengthx, lengthy);//Meshクラスのインスタンス化 /* U,V,P,bの定義 */ #include "creatFields.h" print2dfield(P, "P"); // solution int ntimestep = 500; double dt = 0.001; double rho = 1.0; double visc = 1e-3; // file write FileWriter filewriter2d_; string name = "2DConvectional_diffusion"; // initial condition for (int i = 0; i < U.size(); i++) { for (int j = 0; j < U[i].size(); j++) { if ((U[i][j].x > 0.75 && U[i][j].x < 1.25) && (U[i][j].y > 0.75 && U[i][j].y < 1.25)) { U[i][j].value = 2.0; } } } Unew = U; for (int nt = 0; nt < ntimestep; nt++) { cout << "Iteration no : " << nt << endl; //outcome if (nt % 10 == 0) { filewriter2d_.write2dUVFields(Unew, Vnew, Pnew, nt, name); } U = Unew; V = Vnew; P = Pnew; /* du/dt + udu/dx + vdu/dy= nu ∇^2 u dv/dt + udv/dx + vdv/dy= nu ∇^2 v */ Unew = U - dt * (U && fd::gradX(U)) - dt * (V && fd::gradY(U)) + dt * visc * (fd::laplacian2d(U)); Vnew = V - dt * (U && fd::gradX(V)) - dt * (V && fd::gradY(V)) + dt * visc * (fd::laplacian2d(V)); /* ∇^2 P = 0 */ Pnew = (fd::poissonX(P)) + (fd::poissonY(P)); //ポアソン方程式 } return 0; } |
結果を出力するためにFileWriter.hで
|
1 |
void write2dUVFields(Fields::vectorField2d&, Fields::vectorField2d&, Fields::vectorField2d&, int, std::string&); |
を定義しています。
FileWriter.h
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
#ifndef FILEWRITWE_H #define FILEWRITWE_H #include <stdio.h> #include <iostream> #include <vector> #include <cmath> #include <string> #include <cstring> #include <sstream> #include <fstream> //ファイルの書き込みに必要 #include "Fields.h" using namespace std; using std::vector; using std::string; class FileWriter { public: FileWriter();//constructor virtual ~FileWriter(); //destructor void write1dField(Fields::vectorField1d&, string&); void write2dUVFields(Fields::vectorField2d&, Fields::vectorField2d&, Fields::vectorField2d&, int, std::string&); }; #endif |
FileWriter.cppに処理内容を書きます。
FileWriter::write1dFieldは1次元の計算結果を出力する際には必要でしたが今回は使いません。
FileWriter.cpp
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
#include "FileWriter.h" #include <iostream> FileWriter::FileWriter() { } void FileWriter::write1dField(Fields::vectorField1d& vec, string& name_) { string myfileType = ".dat"; //拡張子 string path = "C:\\work\\C_lang\\20220413_diff_C_puls\\004_NS_Eq_1D_blog\\1DNS\\1DNS\\"; //絶対パス string pathName = path.append(name_).append(myfileType); //"myOutput;" + ".dat" => "myOutput.dat" std::cout << "pathName = " << pathName << " : pathName.size() = " << pathName.size() << std::endl; FILE* outfile; fopen_s(&outfile, pathName.c_str(), "w+t"); //https://www.paveway.info/entry/2018/12/25/cpp_std_string_char std::cout << "outfile = " << &outfile << std::endl; for (int i = 0; i < vec.size(); i++) { double xpos = vec[i].x; double uvel = vec[i].value; if (outfile) { fprintf(outfile, "%5.8lf\t%5.8lf\n", xpos, uvel); } } fclose(outfile); } void FileWriter::write2dUVFields(Fields::vectorField2d& Utemp, Fields::vectorField2d& Vtemp, Fields::vectorField2d& Ptemp, int time_, std::string& name_) { string myfileType = ".dat"; //拡張子 string path = "C:\\work\\C_lang\\20220413_diff_C_puls\\005_NS_eq_2D\\NS2d\\NS2d\\"; //絶対パス ostringstream temp; temp << time_; string pathName = path.append(name_).append(temp.str()).append(myfileType); //std::cout << "pathName = " << pathName << " : pathName.size() = " << pathName.size() << std::endl; //char* cstr = new char[pathName.size() + 2]; // メモリ確保 //std::cout << "cstr = " << &cstr << std::endl; //strcpy_s(cstr, name2.size() + 2, name2.c_str()); FILE* outfile; fopen_s(&outfile, pathName.c_str(), "w+t"); //https://www.paveway.info/entry/2018/12/25/cpp_std_string_char //std::cout << "outfile = " << &outfile << std::endl; // tcplot format - Paraview is an Open Source Software for visualization int NXtemp = Utemp.size(); int NYtemp = Utemp[0].size(); fprintf(outfile, "VARIABLES=\"X\",\"Y\",\"U\",\"V\"\"P\"\n"); fprintf(outfile, "ZONE F=POINT\n"); fprintf(outfile, "I=%d, J=%d\n", NXtemp, NYtemp); for (int i = 0; i < NYtemp; i++) { for (int j = 0; j < NXtemp; j++) { double xpos, ypos, UU, VV, PP; xpos = Utemp[i][j].x; ypos = Utemp[i][j].y; UU = Utemp[i][j].value; VV = Vtemp[i][j].value; PP = Ptemp[i][j].value; //%5.8lf\t fprintf(outfile, "%5.8lf\t%5.8lf\t%5.8lf\t%5.8lf\t%5.8lf\n", xpos, ypos, UU, VV, PP); } } fclose(outfile); } FileWriter::~FileWriter() { } |
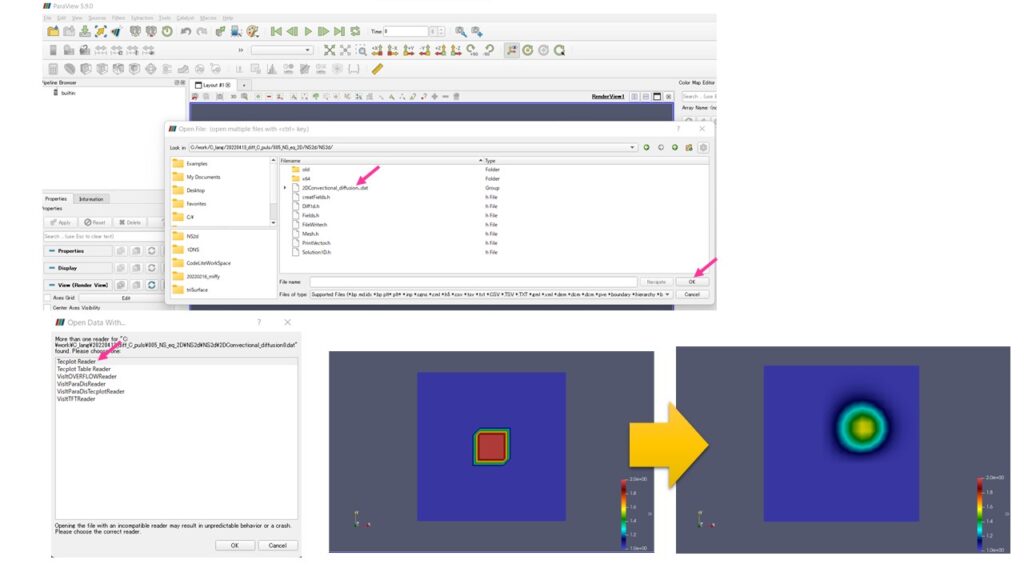
結果をParaViewで確認してみましょう。
【結果】