C++

【オブジェクト指向C++】2次元ナビエストークス方程式(キャビティ流れ)の数値計算

目次
  1. 利用するコード
  2. 解くべき方程式の確認（ナビエストークス方程式とポアソン方程式）
  3. 解くべき方程式の離散化
  4. その前に、初期状態と境界条件を設定
  5. キャビティ流れを解く手順（フロー）

利用するコード

こちらの1次元の移流方程式のコードをベースに2次元ナビエストークスの数値計算が行えるように修正していきます。

プログラム保存先

https://github.com/kamakiri1225/1DNS

main.cpp

creatFields.hを作ってUの設定は別のヘッダーファイルで定義するようにしました。

creatFields.h

さらにプログラム作成途中でU[i].vauleの値を確認したい場合に出力するプログラムをヘッダーファイルに書きました。

main.cppで

によりインクルードしています。

PrintVector.h

main.cppで

の2行でよりでU[i].vauleの値を確認できます。

Mesh.h

Mesh.cpp

Fields.h

Fields.cpp

Diff1d.h

Solution1D.h

Solution1D.cpp

FileWriter.h

FileWriter.cpp

こちらのコードをベースに修正していきます。

解くべき方程式の確認（ナビエストークス方程式とポアソン方程式）

今回解析するのはキャビティ流れと呼ばれる流れです。

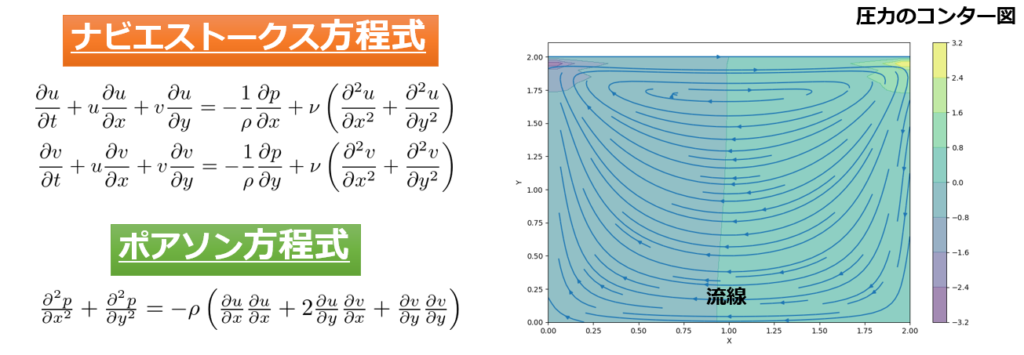
Pythonでもキャビティ流れを行ったのが下記の記事です。
C++はわからなくてもPythonならわかるという方には良い内容です。

あわせて読みたい

【第16回Python流体の数値計算】2次元キャビティ流れをPythonで実装する。

まずは、今回「解くべき方程式」と「変数」が何かを確認しておきましょう。

非圧縮性流体として現象を取り扱う場合には、基本的には以下の2つの式を連立して解きます。
ナビエストークス方程式
\begin{align*}
\frac{\partial \boldsymbol{v}}{\partial t}+(\boldsymbol{v}\cdot\nabla)\boldsymbol{v}=-\frac{1}{\rho}\nabla p + \nu \nabla^2\boldsymbol{v}\tag{1}
\end{align*}

※ナビエストークス方程式は成分の数だけ式があります。

連続の式（非圧縮条件）
\begin{align*}
\nabla\cdot\boldsymbol{v}=0\tag{2}
\end{align*}
実際の流れは、すべての現象が(1)(2)式というわけではないです。
「ニュートン流体」「非圧縮の流れ（近似）」としているとても限定的な流れであることを理解しておきましょう。
もっと詳しく勉強したい方は☟こちらの記事を参考にしてください。
あわせて読みたい
  1. 流体力学の非圧縮性と圧縮性
  2. 非圧縮性流体の基礎方程式

今回は、2次元で計算を行うため少々くどいですが、成分ごとの式を書き下すことにします。

【2次元での計算】
ナビエストークス方程式
\begin{align*}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right) \tag{3}
\end{align*}
\begin{align*}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)\tag{4}
\end{align*}
連続の式（非圧縮条件）
\begin{align*}
\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\tag{5}
\end{align*}
  • ナビエストークスからは2本の式
  • 連続の式から1つの式

が出てくるので、合計で3本の式があります。

未知数は、\(\boldsymbol{v}\)の2つと圧力\(p\)の合計3つです。なので、原理的に未知数である物理量は全て求まることになります。それを各時刻で求めていけば良いという事になります。
しかし、言葉で簡単に言っても、特殊な境界条件や近似を用いないとナビエストークス方程式は解析的に取り扱うことができないのです。つまり、ナビエストークス方程式には一般解が見つかっていないので、実際には数値計算を使って偏微分方程式を取り扱うしかないのが現状です。
しかし、連立方程式を解けばいいと言われてもちょっと困った・・・
なぜなら、(3)(4)式で求めた流速は(5)式を満たす必要があります。
そのように流速を選びながら圧力を同時に決めなければなりません。
考えただけでもちょっと工夫が必要ですよね。。
そこで、以下のようにして考えを改めます。
圧力に関しては非圧縮条件を満たすようにポアソン方程式を解きつつ、求めた圧力に関してナビエストークス方程式を解き流速を求めるという手法をとります。
言葉で説明してもよくわからないかもしれないので、実際にやります(^^)/
(3)式を\(y\)で偏微分
\begin{align*}
&\frac{\partial }{\partial x}\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+u\frac{\partial^2 u}{\partial x^2}+ \frac{\partial v}{\partial x}\frac{\partial u}{\partial y}+v\frac{\partial^2 u}{\partial x\partial y} \\
&= -\frac{1}{\rho}\frac{\partial^2 p}{\partial x^2}+\nu \frac{\partial }{\partial x}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{6}
\end{align*}
(4)式を\(x\)で偏微分
\begin{align*}
&\frac{\partial }{\partial y}\frac{\partial v}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+u\frac{\partial^2 v}{\partial y\partial x}+ \frac{\partial v}{\partial y}\frac{\partial v}{\partial y}+v\frac{\partial^2 v}{\partial x\partial y^2} \\
&=-\frac{1}{\rho}\frac{\partial^2 p}{\partial y^2}+\nu \frac{\partial }{\partial y}\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right)\tag{7}
\end{align*}
このようにして辺々足して、非圧縮条件を使えば、
\begin{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} = -\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right)\tag{8}
\end{align*}
計算はだるいですが、一度やってみてください。
つまり、(3)(4)(5)を解く代わりに以下の式を解けばよいという事になります。
【2次元での計算】※実際に解く方程式
ナビエストークス方程式

\begin{align*}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu \left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} \right) \tag{3}
\end{align*}

\begin{align*}
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right)\tag{4}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
\frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2} =b(x,y) \tag{8.1}
\end{align*}
右辺を\(b(x,y)\)とおいて以下のようにまとめました。
\begin{align*}
b(x,y)=-\rho\left(\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}\frac{\partial v}{\partial x}+\frac{\partial v}{\partial y}\frac{\partial v}{\partial y} \right) \tag{8.2}
\end{align*}
速度については、ナビエストークス方程式を解きつつ、圧力に対してポアソン方程式を連立させながら解くという事になります。
ポアソン方程式の解き方については、以下の記事で解説していますのでまだ読んでいない方はお読みください_(._.)_
では、解くべき方程式がわかったところで、(3)(4)(8.1)(8.2)を離散化して数値計算ができる状態にします。

解くべき方程式の離散化

【2次元での計算】※実際に解く方程式
ナビエストークス方程式
\begin{align*}
& \frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{u_{i,j}^{n}-u_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i+1,j}^{n+1}-p_{i-1,j}^{n+1}}{2\Delta x}+\nu\left(\frac{u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}}{\Delta
x^2}+\frac{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2}\right)\tag{9}
\end{align*}
\begin{align*}
&\frac{v_{i,j}^{n+1}-v_{i,j}^{n}}{\Delta t}+u_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i-1,j}^{n}}{\Delta x}+v_{i,j}^{n}\frac{v_{i,j}^{n}-v_{i,j-1}^{n}}{\Delta y} = \\
& \qquad -\frac{1}{\rho}\frac{p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}}{2\Delta y}+\nu\left(\frac{v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}}{\Delta x^2}+\frac{v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}}{\Delta y^2}\right)\tag{10}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
\frac{p_{i+1,j}^{n+1}-2p_{i,j}^{n+1}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n+1}-2p_{i,j}^{n+1}+p_{i,j-1}^{n+1}}{\Delta y^2} = b_{i,j}^{n}\tag{11.1}
\end{align*}
\begin{align*}
b_{i,j}^{n} = \rho \left[-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
– 2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}\\
– \frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{11.2}
\end{align*}

※非圧縮過程なので$\nabla \cdot \boldsymbol{v}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$

どういった離散化をしているのかを以下でまとめておきました。

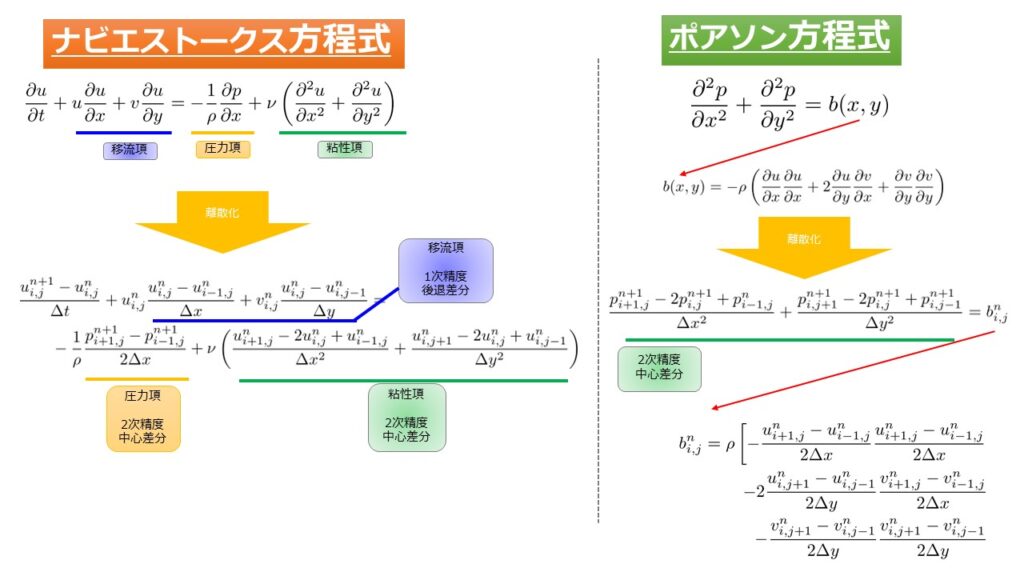
これで離散化は完了ですが、知りたいのは\(n+1\)ステップでの格子点\(i,j\)の流速\(u^{n+1}_{ij}\)、\(v^{n+1}_{ij}\)、圧力\(p^{n+1}_{ij}\)ですので、

以下のように式変形します。

 

【2次元での計算】※実際に解く方程式
ナビエストークス方程式
\begin{align*}
u_{i,j}^{n+1} = u_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(u_{i,j}^{n}-u_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(u_{i,j}^{n}-u_{i,j-1}^{n}\right) \\
& – \frac{\Delta t}{\rho 2\Delta x} \left(p_{i+1,j}^{n}-p_{i-1,j}^{n}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(u_{i+1,j}^{n}-2u_{i,j}^{n}+u_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}\right)\right)\tag{12}
\end{align*}
\begin{align*}
v_{i,j}^{n+1} = v_{i,j}^{n} & – u_{i,j}^{n} \frac{\Delta t}{\Delta x} \left(v_{i,j}^{n}-v_{i-1,j}^{n}\right) – v_{i,j}^{n} \frac{\Delta t}{\Delta y} \left(v_{i,j}^{n}-v_{i,j-1}^{n})\right) \\
& – \frac{\Delta t}{\rho 2\Delta y} \left(p_{i,j+1}^{n+1}-p_{i,j-1}^{n+1}\right) \\
& + \nu \left(\frac{\Delta t}{\Delta x^2} \left(v_{i+1,j}^{n}-2v_{i,j}^{n}+v_{i-1,j}^{n}\right) + \frac{\Delta t}{\Delta y^2}
\left(v_{i,j+1}^{n}-2v_{i,j}^{n}+v_{i,j-1}^{n}\right)\right)\tag{13}
\end{align*}
ポアソン方程式※連続の式（非圧縮条件）
\begin{align*}
p_{i,j}^{n+1}=\frac{(p_{i+1,j}^{n+1}+p_{i-1,j}^{n+1})\Delta y^2+(p_{i,j+1}^{n+1}+p_{i,j-1}^{n+1})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}
\tag{14.1}
\end{align*}
\begin{align*}
b_{i,j}^{n} =  \rho\left[-\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\frac{u_{i+1,j}^{n}-u_{i-1,j}^{n}}{2\Delta x}\\
-2\frac{u_{i,j+1}^{n}-u_{i,j-1}^{n}}{2\Delta y}\frac{v_{i+1,j}^{n}-v_{i-1,j}^{n}}{2\Delta x}-\\
\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\frac{v_{i,j+1}^{n}-v_{i,j-1}^{n}}{2\Delta y}\right]\tag{14.2}
\end{align*}
では、これらを数値計算で解いていきましょう。

その前に、初期状態と境界条件を設定

数値計算をはじめるまえに、初期状態と境界条件を設定する必要があります。

【初期状態】
  • \(u, v, p = 0\)
【境界条件】
  • \(u=1\) at \(y=2\)
  • \(u, v=0\) その他
  • \(\frac{\partial p}{\partial y}=0\) at \(y=0\)
  • \(p=0\) at \(y=2\)
  • \(\frac{\partial p}{\partial x}=0\) at \(x=0,2\)

言葉だけではよくわからないかと思いますので、絵を作成しました。

今回解析するのは「キャビティ流れ」と呼ばれる流れです。

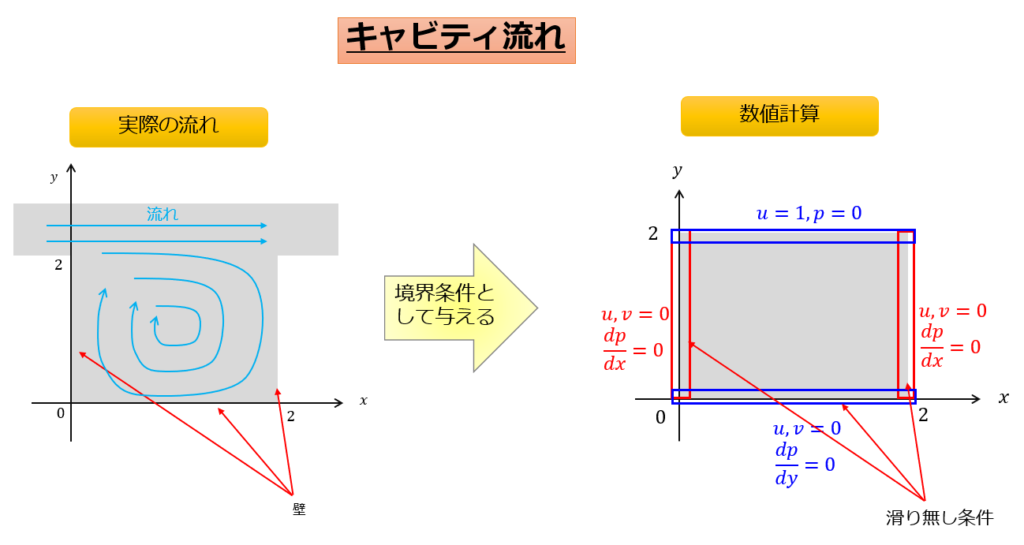
※ちなみに、圧力の基準圧を\(p=0\)としています。
なので、境界条件として\(y=0\)の圧力は\(p=0\)としています。
非圧縮条件で式を解く場合は、圧力の微分の項のみしか意味がないので、基準値は何でもいいんですよね。だから、もし考えている系の基準圧を大気圧（101.25Paくらい）としている場合に、わざわざ境界条件を\(p=101.325kPa\)とする必要はありません。
境界条件に\(p=0\)としておいて、計算された圧力分布は基準圧に対してどうなのかを考えればいいだけです。
（基準圧が\(p=101.325kPa\)なら、分布に\(p=101.325kPa\)を足せばいいだけという意味です）

流体解析に関する境界条件の考え方は非常に見ずかしいので、扱う現象に応じて自身で境界条件を考える必要があります。
ここでは、詳しくは解説しませんが（体系的に解説できるほどの知識もないですが_(._.)_）以下の記事が参考になると思います。

境界条件に関する記事はこちら

 

では、以下で実際にナビエストークス方程式とポアソン方程式を連立させながらGoogle Colaboratoryを使ってPythonのコードを書いていきましょう。

キャビティ流れを解く手順（フロー）

ひとつひとつ解説をしながらコードを書いていきます。
※関数にまとめておいた方がいい部分は関数にまとめます。
今回行う数値計算の解く手順は以下のフローに従っています。
これは「MAC（Marker And Cell）法」と呼ばれる非圧縮流体の解析手法の一種です。
ナビエストークス方程式、およびナビエストークス方程式の発散と連続の式から得られる圧力方程式を連立して計算を行います。
1 2 3 4 5 6
関連記事もどうぞ

COMMENT

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です